Как уже неоднократно отмечалось, для проведения расчетов по адаптивным моделям необходимо задать начальные значения 
, 
, 
и определить оптимальные в некотором смысле параметры 
, 
, 
, а для моделей с многошаговым алгоритмом адаптивного механизма и параметр 
.
В принципе, для достаточно длинных временных рядов выбор начальных значений может быть произвольным. С течением времени влияние начальных значений на прогнозные расчеты в результате многократного сглаживания перестает ощущаться. Однако в экономике часто приходится иметь дело с короткими временными рядами и, поэтому, от выбора начальных значений зависит точность окончательных результатов. Кроме того, при задании начальных значений мы должны учитывать то обстоятельство, что в самонастраивающейся структуре адаптивного механизма предусмотрен вариант построения адаптивной модели с постоянными коэффициентами, которые по схеме построения такого варианта полагаются равными начальным значениям. Если же выбор начальных значений осуществлять произвольным образом, например, положить все компоненты вектора равными нулю, то, очевидно, что модель с нулевыми коэффициентами не может представлять по точности предсказания альтернативу модели с переменными коэффициентами. Следовательно, процедура, основанная на произвольном выборе начальных значений, исключает из схемы построения модели важный вариант ее возможной структуры, ухудшая в конечном итоге наследственные свойства адаптивного механизма. Поэтому, в силу приведенных здесь доводов, а также учитывая, что рассматриваемые адаптивные алгоритмы являются рекуррентными вариантами взвешенного МНК, будем для ускорения сходимости к оптимальным оценкам в качестве задавать матрицу, обратную матрице системы нормальных уравнений обычного МНК
. (5.68)
В качестве и выбираются векторы коэффициентов регрессионной модели, вычисленные с помощью МНК по данным одних и тех же временных рядов
, (5.69)
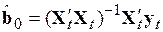, (5.70)
где 
вектор-столбец оценок коэффициентов регрессионной модели;
вектор-столбец значений зависимой переменной в момент времени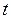 
;
матрица значений независимых переменных из 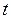строк
.
Начальные значения, задаваемые в виде (6.68)–(6.70), позволяют в структуре возможных вариантов адаптивной модели предусмотреть регрессионную модель с постоянными коэффициентами, определяемыми по МНК, как альтернативную модели с переменными коэффициентами. Это является убедительным аргументом в пользу такого способа определения начальных значений. Кроме того, известно, что именно этот способ обеспечивает быструю сходимость к оптимальным оценкам МНК.
Для определения оптимальных значений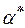 
, 
, 
, 
проще всего применить общеизвестный метод перебора. Применение этого метода предполагает наличие критерия, с помощью которого можно из двух наборов 
, 
, 
, 
и 
, 
, 
, 
различных значений параметров адаптации выбрать наилучший в некотором смысле. В принципе, критерий настройки не обязательно должен быть идентичным по своей структуре функционалу экстремальной задачи. Учитывая это замечание, критерии можно строить таким образом, чтобы они ориентировали настройку параметров адаптации на повышение определенных характеристик точности прогнозных расчетов. Рассмотрим три возможных варианта:
, (5.71)
, (5.72)
, (5.73)
где 
, 
.
Первый критерий представляет собой сумму модулей ошибок прогнозирования и используется в тех случаях, когда за счет настраиваемых параметров необходимо получить минимально допустимую в рамках данной модели сумму прогнозных ошибок по всей обучающей последовательности наблюдений. Второй критерий – это сумма модулей максимальных ошибок прогнозирования. Причем, максимальная ошибка выбирается среди ошибок прогнозирования, рассчитанных для скользящего интервала длиной 
. Третий критерий аналогичен второму, но только в нем суммируются относительные максимальные ошибки прогнозирования. Применение двух последних критериев следует рекомендовать в тех случаях, когда 
и требуется, чтобы уровень ошибки предсказания построенной модели был по возможности равномерно минимальным для всего периода упреждения.
Для всех трех критериев в качестве обучающей последовательности используются первые 
наблюдений, а в качестве контрольной – группа из последних наблюдений. Возможны и другие способы формирования обучающей и контрольной последовательности, например, деление всего выборочного множества наблюдений на две равных части – обучающую и контрольную.
Настройка параметров адаптивного механизма заключается в определении оптимального набора значений 
путем решения экстремальной задачи
, (5.74)
в которой в качестве целевого функционала используется любой из выше- приведенных критериев. В (5.74) 
представляет собой прямое произведение множеств
, (5.75)
где 
(
– достаточно малая положительная величина),
,
.
Для решения этой задачи методом прямого перебора на множестве значений строится сетка
, (5.76)
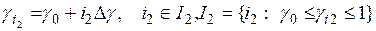, (5.77)
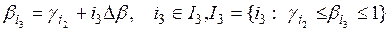, (5.78)
, (5.79)
где 
– заданный шаг изменения соответствующего параметра;
, 
, 
– нижние границы параметров.
Для каждого узла 
сетки (5.76)–(5.79) по рекуррентным формулам настраиваемого адаптивного алгоритма при заданных начальных значениях , , вычисляется последовательность оценок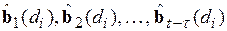 
, используемых в расчетах прогнозных серий 
, 
по значений в каждой. Определенные таким образом серии прогнозных расчетов используются далее для расчета величины выбранного критерия 
. Все полученные значения критерия (их число определяется количеством узлов сетки) сравниваются между собой, что позволяет среди узлов 
, 
(
– множество порядковых номеров, присвоенных узлам сетки) определить такой 
, для которого 
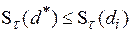для всех . Так определенный вектор параметров считается оптимальным. Его точность определяется задаваемым при построении сетки шагом изменения настраиваемых параметров.
6. ПРОГНОЗИРОВАНИЕ СЕЗОННЫХ КОЛЕБАНИЙ
6.1. Моделирование периодических колебаний
Пусть значения временного ряда 
колеблются около среднего значения 
. Изобразим траекторию этого ряда в виде графика, представленного на рис. 6.1. Данная траектория вряд ли может являться реализацией реального процесса, но рисунок хорошо иллюстрирует вводимые ниже определения.
Периодом называется интервал времени, необходимый для того, чтобы значения временного ряда начали повторяться. Его обычно обозначают Р. Временной ряд, траектория которого изображена на рис. 6.1, имеет период Р=10.
Период измеряется числом единиц времени за цикл. Если временной ряд имеет период Р, то и 2Р, и 3Р, и т.д. также являются его периодом. В общем случае ряд считается периодическим, если выполняется равенство
, где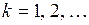 
Частотой называется величина, обратная периоду. Ее обозначают 
и она равна 
. Частота указывает число повторений цикла в единицу времени. В рассматриваемом случае 
. Очевидно, что терминами «период» и «частота» можно пользоваться как взаимозаменяемыми.
 |
 |
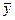
0 2 7 12
Рис. 6.1. График периодической функции
В частном случае временной ряд из констант 
(
) можно считать периодическим с частотой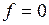 
.
Амплитудой периодического ряда называется отклонение от среднего значения временного ряда до пика или впадины. Амплитуду принято обозначать через 
.
Фазой называется расстояние между началом отсчета времени и ближайшим пиковым значением и обозначается 
.
Периодически временные ряды могут флуктуировать возле возрастающего или убывающего среднего.
 | ||
 |
В экономике также встречаются временные ряды с возрастающей или убывающей амплитудой.
 | ||
 |
Если временной ряд не имеет тренда среднего значения и дисперсия постоянна (т.е. среднее и дисперсия не зависят от времени), то такие временные ряды называют стационарными.
Если при анализе временного ряда возникает ситуация, когда тренд нужно исключить, то это легко сделать, построив регрессию 
по МНК и перейдя к остаткам 
. Альтернативный подход, позволяющий исключить тренд, предусматривает переход к разности 
. В общем случае стационарный временной ряд можно задать, используя четыре выше введенных параметра
. (6.1)
Такая форма представления временного ряда называется гармоническим представлением.
Для временного ряда, траектория которого изображена на рис. 6.1, если 
, то 
, так как 
.
Периодические функции удобно выражать через угловую частоту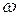 
, задаваемую радианами в единицу времени
, 
.
Если использовать угловую частоту, то модель временного ряда можно записать в виде
, (6.2)
где 
является фазой.
Последнее уравнение часто записывают через тригонометрические функции в виде
, (6.3)
где 
, 
.
Эта запись получена с использованием тригонометрического тождества
. (6.4)
Обычно временной ряд представляет собой сумму многих периодических рядов. Согласно одной из самых распространенных моделей стационарный временной ряд представляет собой бесконечную сумму периодических рядов
, 
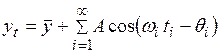(7.5)
или
. (7.6)
Теоретически можно показать, что любой стационарный временной ряд может быть с любой точностью аппроксимирован бесконечным рядом синусоид и косинусоид. Такое представление называют рядом Фурье. Разработан мощный математический аппарат исследования этих рядов. Однако временные ряды в экономике слишком коротки, чтобы можно было использовать этот аппарат. Поэтому рассматриваются другие модели.
6.2. Аддитивная и мультипликативная модели
временного ряда
Построение аддитивной и мультипликативной моделей (6.1), (6.2) сводится к расчету значений трендовой (
), сезонной (
), случайной (
) компонент для каждого уровня ряда и предполагает выполнение следующих шагов:
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты .
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (
) в аддитивной или (
) в мультипликативной модели.
4. Аналитическое выравнивание уровней () или () и расчет значений с использованием полученного уравнение тренда.
5. Расчет полученных по модели значений (
) или (
).
6. Расчет абсолютных и/или относительных ошибок.
6.3. Моделирование сезонных колебаний