Погрешности значения функции

При вычислении значения функции в точке (считаем приближенным значением точного числа ) возникают погрешности – предельная абсолютная и предельная относительная . Выразим эти погрешности через погрешности числа (будем полагать, что функция дифференцируема в точке ).

Так как функция дифференцируема в точке , то

, (4.1)

где мало при малом (иными словами, слагаемым в формуле (4.1) можно пренебречь, если мало).

Учитывая равенство (4.1), истинная абсолютная погрешность будет оцениваться неравенством (приближенным)

,

откуда по определению предельной абсолютной погрешности

. (4.2)

Предельная абсолютная погрешность значения функции в точке ( – приближенное число) равна произведению модуля производной этой функции в точке на предельную абсолютную погрешность числа .

Соответственно предельная относительная погрешность вычисляется следующим образом

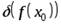= . (4.3)

Найдем с помощью формул (4.2), (4.3) погрешности значений основных элементарных функций.

Пусть ( – действительное число). Тогда

, .

В частности при : .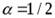

Пусть . Тогда

, .

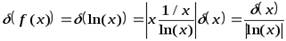Пусть 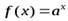. Тогда

, .

В частности, если , то .

Аналогично определяются погрешности значений других основных элементарных функций (см. таблицу 4.1).

Таблица 4.1.

№

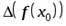
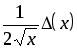
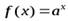
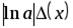
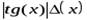
Пример 4.1. Дана функция . Протабулировать ее на отрезке 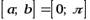(считать ), разбив его на равных частей (все расчеты проводить с 4 знаками после запятой). Вычислить предельные абсолютные, относительные погрешности значений функции в узлах табулирования.

Решение: Протабулировать функцию на отрезке 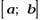с постоянным шагом означает составить таблицу значений 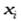, 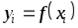(точки 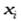называются узлами табулирования), где

. (4.4)

В нашем случае , , ; узлы определяются следующим образом:

. (4.5)

Вычислим значения функции в узлах табулирования (4.5):

.

Имеем , ;

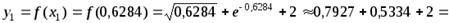, 3,3261,

,

и так далее.

Все вычисления значения функции в узлах табулирования заполняем в таблицу 4.2.

Учитывая формулы (4.2), (4.3), находим погрешности в узлах (4.5) (при этом число можно считать точным, а тогда ; в остальных же узлах (4.5) ,00005)

, .

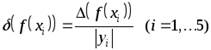Таблица 4.2.

i
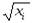
	0,6284	0,7927	0,5334	3,3261	4,8678	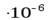1,46
	1,2568	1,2111	0,2846	3,4057	8,0695	2,37
	1,8852	1,3730	0,1518	3,5248	1,0618	0,3
	2,5136	1,5854	0,0809	3,6663	1,1724	0,32
	3,1420	1,7726	0,0432	3,8158	1,1944	0,31

 

Метод исключения при известной среднеквадратичной ошибке:

Обозначим "выпадающее" значение через х_вып, а все другие результаты измерения через x₁, x₂,..., х_n. Определим среднее арифметическое значение

 

и сравним абсолютную величину разности х_вып - с величиной . Для полученного отношения

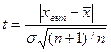(1)

определим вероятность 1-2Ф(t) с помощью таблицы вероятности.

 

Это даст вероятность того, что рассмотренное отношение случайно примет значение, не меньше чем t, при условии, что значение х не содержит грубой погрешности (ошибка результата х_вып только случайная).

Если подсчитанная указанным образом вероятность окажется очень малой, то "выпадающее" значение содержит грубую ошибку и его следует исключить из дальнейшей обработки результатов измерений.

Как предельную величину "малости" обычно выбирают одно из трех значений вероятности:

5% уровень (исключаются результаты, которые содержат погрешности, вероятность появления которых меньше 0,05);

1% уровень;

0,1% уровень.

При избранном уровне a малых вероятностей "выпадающее" значение х_вып считают содержащим грубую ошибку, если для соответствующего отношения t вероятность 1-2Ф ( t)<α. При этом говорят, что значение х_вып содержит грубую ошибку с надежностью вывода Р = 1 - a. Значение t = t (P), для которого

 

 

1-2Ф(t) = a и, значит, Ф(t) = Р, называется критическим значением отношения при надежности Р.

Так, если a= 0,01 (1% уровень), то Р = 0.99, критическое значение t = t (P) = 2,576, и как только отношение превысит это критическое значение, мы можем исключать из рассмотрения результата х_вып с надежностью вывода 0,99.

 

Исходя со сделанных выводов методику определения "выпадающего" результата измерения для заданного предельного уровня вероятности можно представить в таком виде:

1. Определяется вероятность надежности вывода Р = 1 - a = 2Ф(t)

2. По таблице определяется критическое значение t_кр= t (P).

3. По формуле (1) рассчитывается отношение t.

4. Проверяется выполнение условия t>t_кр. Если оно выполняется, то принимается вывод о том, что "выпадающее" значение результата измерения х_вып содержит грубую ошибку и этот результат исключается из дальнейшего рассмотрения. Если это условие не выполняется, то "подозрительный" результат измерения остается в числе обрабатываемых результатов.

 

Метод исключения при неизвестной среднеквадратичной ошибке:

Если величина среднеквадратичной ошибки заранее неизвестна, то она оценивается по результатам измерений

(2)

 

При этом абсолютную величину разности | х_вып - х | между "выпадающим" значением х_вып и средним значением x других (приемлемых) результатов измерений делят на полученное значение s и полученное отношение

 

t = | x_вип – x | / s (3)

 

сравнивают с критическим значением t_кр(P) (с соответствующих таблиц), которое зависит уже не только от значения вероятности надежности вывода Р, но и от числа n результатов измерений.

Методика определения "выпадающего" результата измерения при неизвестной среднеквадратичной ошибке аналогичная рассмотренной раньше с учетом сделанных замечаний и может быть представлена в таком виде:

1. По заданному значению предельной вероятности a определяется вероятность надежности вывода Р = 1 - a = 2Ф(t)

2. По таблице при заданном числе измерений n определяется критическое значение t_кр = t (P).

3. По формуле (2) рассчитывается среднеквадратичное отклонение s

4. По формуле (3) рассчитывается отношение t.

5. Проверяется выполнение условия t>t_кр. Если оно выполняется, то принимается вывод о том, что "выпадающее" значение результата измерения х_вып содержит грубую ошибку и этот результат исключается из дальнейшего рассмотрения. Если это условие не выполняется, то "подозрительный" результат измерения остается в числе обрабатываемых результатов.

 

1.2. Проверка нормальности распределения.

 

Если результаты эксперимента вызывают сомнение в нормальности закона распределения случайных ошибок, то для решения вопроса о пригодности или непригодности нормального закона распределения надо сделать довольно большое число измерений и применить какой нибудь из существующих критериев.

Критерий согласия χ²

Для использования этого критерия результаты измерений группируются по интервалам таким образом, чтобы эти интервалы покрывали всю ось (-∞, +∞) и чтобы количество данных в каждом интервале было довольно большим (в пределах 10). Для каждого интервала (х_i-1, х_і) подсчитывают число результатов измерения, которые попали в этот интервал. Потом вычисляют вероятность р попадания в этот интервал при нормальном законе распределения вероятностей:

 

р = Ф[(х_і - )/s ] - Ф[(х_і-1 - )/s ]

где - среднее арифметическое значение результатов измерения;

s - среднеквадратичная ошибка;

Ф - интеграл вероятностей.

После этого вычисляют сумму

где l - число всех интервалов;

n - число всех результатов измерений.

Если сумма окажется больше критического значения χ² при некоторой доверительной вероятности Р и числе мер свободы k = l - 3, то с надежностью Р можно считать, что распределение вероятностей случайных ошибок в серии измерений, которые рассматриваются, отличается от нормального.

При отсутствии достаточных оснований для того, чтобы отвергнуть гипотезу о нормальном распределении случайных ошибок измерения, эта гипотеза принимается, поскольку в обычных ситуациях эта гипотеза часто может быть обоснована теоретически.

Приближенный метод проверки.

Применение критерия согласия требует довольно значительных расчетов.

Как приближенный метод проверки нормальности распределения применяют метод, связанный с оценками центральных моментов третьего и четвертого порядков. В случае нормального распределения случайных ошибок эти моменты равны соответственно

Оценками этих моментов по результатам эксперимента служат эмпирические центральные моменты

μ _к = { (х_і – m(х))^к / n}

В случае нормального распределения должно выполняться приблизительно равенство

μ ₃ ≈ 0, μ ₄ ≈ 3s⁴

Для удобства сравнения подсчитывают безразмерные характеристики: показатель асимметрии

g_s = μ ₃/s³

и эксцесс

E= μ ₄ /s⁴ -3

где s - среднеквадратичная погрешность.

Обе характеристики должны быть малые, если распределение нормальное. О малости этих характеристик обычно судят в сравнении их с их среднеквадратичными ошибками, соответственно равными

 

6(n-1)/[(n+1)(n+3)] - для g_s

 

24n(n-2)(n-3)/(n-1) (n+3)(n+5) - для Е

 

где n - количество измерений.

Если хотя бы одна из указанных характеристик по абсолютной величине значительно (в 2-3 раза) превосходит свою среднеквадратичную ошибку, то нормальность закона распределения нужно подвергнуть сомнению и провести более тщательный анализ результатов эксперимента (например, по χ- квадрат критерию). В другом случае для такого сомнения нет оснований.

 

1.3. Способы оценивания и исключение систематических погрешностей.

Оценить и исключить систематические погрешности, т.е. погрешности, которые остаются постоянными или закономерно изменяются при повторных измерениях в одинаковых условиях, способом многоразовых наблюдений нельзя. Результат одного наблюдения можно записать как:

Q_і = Q_ист + Δ_іслуч + Δ_сист

 

где Δ_іслуч - реализация случайной погрешности, Δ_сист - постоянная систематическая погрешность.

Если провести n наблюдений и взять среднее арифметическое, то будем иметь

_ист + Δ_іслуч + Δ_сист

В связи с разными знаками реализации случайной погрешности случайная составляющая с ростом n уменьшается, а систематическая погрешность будет оставаться неизменной.

Систематическая погрешность измерений редко может быть определенна в целом, а не суммированием отдельных составляющих. Это можно осуществить, если выполнить измерение более точным методом с использованием более точных средств измерений. Значительно чаще приходится находить состав систематической погрешности. Для этого необходимо понимать принцип работы средств измерений и физические процессы, которые протекает в измерительных цепях. Полностью исключить систематическую погрешность путем введения поправки нельзя, поскольку поправка также определяется с некоторой погрешностью. Таким образом, всегда остаются не исключенные остатки систематической погрешности. Систематические погрешности могут быть связаны с каждым из элементов процесса измерений: несовершенством модели объекта измерений; несовершенством метода измерения; средством измерения, изменением внешних условий, личными качествами наблюдателя.

Для выявления, оценки и исключения систематических погрешностей необходимо тщательное изучение применяемых методов, средств и условий измерения. Однако можно указать простейшие общие способы выявления, оценки и исключения систематических погрешностей.

1. Исключение систематической погрешности при измерении путем применения соответствующих методов и приемов, например метода замещения, метода компенсации погрешности по знаку, использующего два измерения, вследствие которых систематическая погрешность входит с разными знаками. Эти методы позволяют исключить постоянную систематическую погрешность, выявление которой представляет наибольшие трудности, непосредственно в процессе измерения, а не путем обработки результатов.

2. Оценка систематической погрешности путем применения более точного метода и средства измерения.

Систематическая погрешность, если пренебрегать погрешностью сверки, будет равная Δ_сист = где - результат точного измерения.

3. Выявление систематической погрешности в результатах измерений с многоразовыми наблюдениями одной физической величины двумя независимыми методами. Для этой цели разработаны статистические методы обработки результатов, методы корреляционного и регресийного анализа.

4. Оценивание систематической погрешности расчетным путем. Для этой цели выражают значение измеряемой величины, которая с учетом воздействующего фактора ("измеренное значение") и при его отсутствии ("истинное значение"). Разность первого и второго значений и будет абсолютная систематическая погрешность

Δ_сист = Q_изм – Q_ист.

5. Исключение систематической погрешности введением поправки. Поправка С=-Δ_сист бывает известна с ограниченной точностью и характеризуется средним значением со среднеквадратичному отклонению=σ(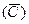. При введении поправки систематическая составляющая погрешности уменьшается, а дисперсия результата измерения возрастает. Критерием целесообразности введения поправки есть интервал суммарной погрешности измерений. Поправку необходимо вводить, если

 

где t_p и t_p1 - величины, которые зависят при одинаковой доверительной вероятности от законов распределения i ;

и - оценки среднеквадратичных значений случайных погрешностей результата измерений величины поправки.

Условием целесообразности введения поправки при t_p = t_p1 есть

 

1.4 Формы представления результатов измерений и показатели точности

Чтобы результаты, полученные в разных лабораториях могли сопоставляться, формы представления результатов измерений и показатели точности регламентируются документами. Согласно стандарту результат измерения представляется в виде значения измеряемой величины и показателей точности. В зависимости от сложности и ответственности измерений используются показатели точности измерения разной сложности:

- интервалы, в которых с заданной вероятностью находится суммарная погрешность измерения Δ или ее систематическая составляющая Δ_сист

- оценки среднеквадратичного значения случайной Δ_случ и систематической + Δ_сист составной погрешностей;

- плотность распределения систематической f(Δ_сист) или случайной f(Δ_случ) составляющих погрешностей

Наиболее распространены технические измерения, которые выполняются однократно. Их погрешность определяется погрешностью средств измерений. Эта погрешность известна до измерения из нормативно технической документации. Записывается результат измерения и погрешность в виде границы допускаемой суммарной погрешности. Вероятность не указывают, предполагается ее значение Р = 0,997.

Числовое значение результата измерения должно быть представлено с учетом погрешности, с которой это измерение выполнено. Младший разряд результата должен отвечать разряду погрешности.

При выполнении технических измерений возможно два случая:

В первом случае измерение выполняется прибором, который есть в наличии, класс точности которого δ. Максимальная погрешность прибора

Δ_max = δ· A_k /100

где A_k- конечное значение шкалы прибора. Результат измерения записывают в форме A ± Δ_max

где A - свидетельство прибора.

 

Во втором случае измерение должно быть выполненно с погрешностью, которая не превышает заданную (допустимую). Выбирают соответствующий измерительный прибор, погрешность которого Δ_max ≤Δ_доп и с помощью однократного измерения получают результат A ± Δ_max.

Нужно иметь в виду, что погрешность, которая определяется при технических измерениях есть суммарной, т.е.

Δ_max =Δ_случ + Δ_сист