Лекция 15. Автокорреляция и ее вычисление
|
Пусть задана бесконечная последовательность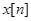 
. По ней строится автокорреляционная функция 
. Эта функция играет огромное значение в при обработке сигналов. Основное назначение - отыскание максимумов функции 
, которые интерпретируются как аналоги периодов. Из неравенства Коши следует, что 
. В точках максимума 
сдвинутая на 
исходная последовательность "похожа" на исходную. В качестве примера рассмотрим фрагмент звукового файла с записью звука "а". Этот сигнал не является периодическим в математическом смысле слова, однако, визуально такая периодичность просматривается. Значения периода находятся по максимумам соответствующей автокорреляционной функции. Найдем преобразование Фурье от . Для непрерывного случая эта задача рассматривалась выше. Положим 
. Теперь 
, где 
- свертка последовательностей.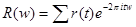 
= 
. С другой стороны, 
= 
. Это означает, что 
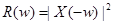. Если исходная последовательность вещественная, то 
и
(1)
Случай конечной последовательности
При практическом использовании автокорреляционной функции мы имеем дело с конечными последовательностями. Пусть дана последовательность 
. Определим функцию 
(как обычно, последовательность считается периодической). Повторяя предыдущие рассуждения, получим для конечного преобразования Фурье в вещественном случае аналог (1)
(2)
Если для заданного 
существует схема БПФ, то выгоднее для отыскания значений 
сначала найти преобразование Фурье от исходной последовательности, а затем воспользоваться (2) для отыскания значений функции.
В случае конечных последовательностей мы имеем дело с циклической сверткой. Для того, чтобы избавиться от эффекта цикличности, используется следующий прием. Вместо исходной последовательности длины берется последовательность 
длины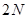 
. Если используются значения 
, то при их вычислении эффект цикличности не имеет места.
Практическое оценивание частот
В предыдущий рассмотрениях не учитывалась частота выборки 
из исходного непрерывного сигнала. Имеем
. Рассматривая последнее выражение как приближение соответствующего интеграла, получим, что данный коэффициент соответствует частоте 
. При выборе значения следует учитывать следующее обстоятельство - увеличение повышает разрешающую способность, но при этом происходит усреднение по длине окна.
Если для оценки периода использована автокорреляционная функция, то максимуму этой функции в точке 
отвечает частота 
Лекция 17. Применения автокорреляционной функции
Частота основного тона
|
|
В качестве примера укажем применение автокорреляционной функции для вычисления частоты основного тона речевого сигнала. В настоящее время нет математического определения этой частоты. В предыдущей лекции приведен пример вида сигнала, соответствующего произнесению звука "а". На рисунке просматриваются периодический характер колебаний. Фактическое значение найденной частоты зависит от способа оценки. Простейший - подсчет с помощью преобразования Фурье. Это показано на рисунке. Основному тону соответствует частота, для которой достигается максимум. Этот способ не годится, если вблизи максимума график является пологим. Рассмотрим другие подходы.
Амплитудное ограничение. Выбирается порог, и исходный сигнал заменяется последовательностью нулей и единиц: в точках, где сигнал превышает порог, ставится 1, в остальных точках - 0. Получается сигнал вида приведенного на рисунке. После этого ищут максимумы для автокорреляционной функции сигнала. При этом можно не прибегать к схемам, основанным на БПФ, поскольку в этом случае все сводится лишь к операциям сложения.
Пересечение с нулем. Рассмотрим график функции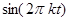 
. Значение 
можно оценить по формуле 
, где - длина интервала, а 
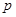- количество переходов через 0. Этот способ применяют к речевому сигналу. Для того, чтобы исключить из рассмотрения мелкие колебания в окрестности 0, сигнал пропускают через фильтр низких частот.
Поиск сигнала с помощью кросс корреляционной функции
К рассматриваемому кругу вопросов примыкает следующая задача. Пусть имеется входная последовательность 
большой длины и образец 
значительно меньшей длины 
. Требуется выяснить, присутствует ли образец во входной последовательности, и если присутствует, определить его место положения. Фактически, Wavelet преобразование первоначально возникло как обобщение этой задачи. Очевидно, что при наличии искажений, задача не имеет точного решения. Можно говорить лишь о близости в некотором смысле отрезка входной последовательности и образца. В вещественном случае в качестве меры близости часто используют функцию 
и ищут значения аргумента, для которых эта функция имеет локальный максимум. После этого, соответствующие отрезки входной последовательности подвергаются дополнительному исследованию. Наша ближайшая цель - указать методы, с помощью которых осуществляется подсчет значений 
, поскольку непосредственные вычисления требуют значительных ресурсов.
Процессор малой мощности
Предположим, что процессор быстро производит лишь операции сложения и вычитания с целыми числами. Для подсчета произведения используется следующий прием. Имеем 
. В памяти хранятся значения квадратов возможных значений, а деление на 4 в двоичном коде сводится к логическому сдвигу на две позиции.
Использование БПФ
Даже при наличии мощного процессора непосредственный подсчет всех нужных значений является трудоемкой задачей. Для уменьшения числа умножений используется следующий подход. Образец заменяется последовательностью 
длины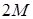 
. Из входной последовательности образуют последовательности длины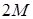 
, 
. После этого подсчитывается циклическая свертка 
Для отыскания значений свертки используется БПФ. Для этого число 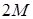должно обладать соответствующими арифметическими свойствами. Покажем теперь, как по найденным значениям 
подсчитываются значения . Это проще всего продемонстрировать на примере 
. Имеем
, 
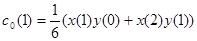
. Точно также, 
. Теперь мы можем найти значения 