Блочные коды. Методика матричного кодирования.

Толстиков А.В. ПАМ

Курс 3. Семестр 5. Лекция 2. Тема. Основы теории групповых кодов.

1. Основные понятия передачи информации. Кодирование и декодирование.

2. Блочные коды. Методика матричного кодирования.

3. Групповые коды. Таблица декодирования.

4. Коды Хэмминга.

Биргоф Г., Барти Т., c.236-257

Основные понятия передачи информации. Кодирование и декодирование.

Кодирование это преобразование информации из одного вида в другой. Оно проникло во все информационные технологии:

представление данных произвольной природы (чисел, текста, графики и т.п.) в памяти компьютера;

защита информации от несанкционированного доступа;

обеспечение помехоустойчивости при передачи информации по каналам связи;

сжатие информации в базах данных.

Конечное множество A различных символов называем алфавитом. Пусть дан алфавит A = { a ₁, a ₂,…, a_n). Символы алфавита называют буквами алфавита. Словом длины k в алфавите А называется любую конечную упорядоченную последовательность из k символов алфавита A (возможно и равных).. Множество всех слов в алфавите А обозначаем символом S (A). Пустым словом называем слово, не содержащее ни одной буквы. Оно обозначается символом L: LÎ S (A). Длину слова a обозначаем символом |a|. Длина пустого слова равна нулю.

Пусть заданы алфавиты A = { a ₁, a ₂,…, a_n), B = { b ₁, b ₂,…, b_m). Пусть дана функция F: S¢ ® S (B), где S¢ некоторое множество слов алфавита А. Тогда функцию F называем кодированием, слова множества S¢ называются сообщениями, образы слов b = F (a) Î S (B) называются кодами или кодовыми словами.

Обратная функция F ^{- 1}, если она существует называется декодированием.

Если | B | = m, то называется m - ичным кодированием. Если B = {0, 1}, то кодирование называется двоичным кодированием.

В общем виде задачу кодирования можно сформулировать следующим образом: при заданных алфавитах A, B и множестве S¢ сообщений найти такое кодирование, которое обладает определенными свойствами.

Критерий оптимальности, минимизация длины кодовых слов при выполнении определенных характеристических свойств. С войства, которыми должны обладать кодирования можно отнести к одному из следующих:

существование декодирования;

помехоустойчивость или исправления ошибок;

заданная сложность или простота кодирования и декодирования.

В этой лекции рассматриваем в основном коды, обладающие вторым из этих свойств. Будем предполагать, что алфавиты А и В двоичные, т.е. А = В = {0,1}. Множество всех слов длины n обозначаем символом Bⁿ.

Каждое слово a длины n это упорядоченная последовательность n символов алфавита В a = a ₁ a ₂… a_n.

Два слова и длины называются равными, если равны их все соответствующие символы:

a = a ₁ a ₂… a_n, b = b ₁ b ₂… b_n, a = b Û (" i = 1,..., n)[ a_i = b_i ].

Теорема 1. Всего имеется 2 ⁿ - различных двоичных слов длины n в алфавите B = {0,1}.

Доказательство следует из того, что каждый символ a_i в слове a может принимать ровно два значения 0 и 1.

Можно считать, что В = {0,1} = Z₂ - поле классов вычетов по модулю 2. Cлова длины n можно рассматривать, как векторы n -мерного координатного пространства Bⁿ над полем Z₂. Тогда справедливы следующие утверждения:

Теорема 2. Множество Bⁿ всех слов длины n с элементами из Z₂ аддитивная абелева группа порядка 2 ⁿ относительно операции побуквенного сложения слов по модулю 2.

Теорема 3. Множество Bⁿ всех слов длины n с элементами из Z₂ векторное пространство размерности n над полем Z₂ относительно операции побуквенного сложения слов по модулю 2 и умножения на элементы из Z₂.

Определение 1. Весом w (a) слова a = a ₁ a ₂… a_n называем количество букв в слове a, которые равны 1.

Определение 2. Расстоянием Хемминга d (a, b) между словами a = a ₁ a ₂… a_n, b = b ₁ b ₂… b_n,называем сисло попарно различных букв в словах a и b, т.е. вес d (a, b) равен количеству позиций, в которых a_i ¹ b _i.

Теорема 4. Расстояние d (a, b) между словами длины n с элементами из Z₂ равно весу разности этих слов, т.е

d (a, b) = w (a - b).

Доказательство. Доказательство утверждения следует из того, что в поле Z₂ разность a_i - b_i элементов a_i, b_i равна 1 тогда и только тогда, когда a_i ¹ b _i. Тогда число единиц в разности равно числу попарно различных букв в словах a и b, т.е. равна весу разности. 

Пример 1. Пусть a = 10111001, b = 00110011 слова длины 8. Тогда w (a) = 5, w (b) = 4, d (a, b) = 3,a-b = 10001010,

w (a - b) 3.

Все слова длины n можно геометрически интерпретировать как вершины n- мерного гиперкубам, а тогда минимальное число ребер разделяющее вершины a и b гиперкуба равно расстоянию Хемминга d (a, b)между соответствующими словами.

Рассматриваем проблему передачи информации по каналу связи (радиоканалы, оптико-волоконные каналы, линии связи, связи компьютера с периферийными устройствами), в котором могут возникать различные помехи. Практически все каналы связи не идеальны, так как любой сигнал с некоторой ненулевой вероятностью может быть принят неправильно. При цифровой обработке информации обычно передаются слова, которые являются символами 0 и 1. Если передаваемые сообщения являются длинными, то незначительная вероятность ошибки на один символ может привести к значительным искажениям посылаемого сообщения. Отметим, что при передачах сигналов по спутниковым средствам связи на них действуют внешние электромагнитные сигналы, космические лучи, внешние поля, и поэтому сигналы могут отразиться и измениться до неузнаваемости.

Рассмотрим простейшую схему канала связи (Рис. 3).

1) На вход канала поступает передаваемое сообщение (слово a).

2) Слово кодируется устройством (функцией Е) в передаваемое кодированное сообщение (кодовое слово b).

3) Кодированное сообщение (кодовое слово b) передается по линии связи и при передаче по каналу связи на его действуют искажения, возникающие в линии связи и внешние помехи.

4) При выходе с линии связи получаем искаженное принятое сообщение (слово b').

5) Слово декодируется устройством (функцией D), которая должна обнаруживать и исправлять ошибки, возникшие при передаче сообщения, на выходе получаем декодированное сообщение (слово a'), которое в идеале должно совпадать со словом a'.

Чтобы обеспечить надежные каналы связи необходимо решить две задачи:

1. Обнаружит ошибки в полученном сообщении по каналу связи;

2. Исправить полученное сообщение.

При математическом анализе канала связи пользуются упрощенными моделями канала связи. Простейшей моделью канала связи является двоичный симметричный канал связи.

В нем двоичные сигналы 0, 1 последовательно передаются по линии связи от передатчика на приемник. При этом считается, что каждый сигнал принимается правильно с вероятностью p и ошибочно с вероятностью q = 1 - p. Сверх того предполагается, что ошибки в передаче последовательных сигналов происходят независимо.

Определение 3. Пусть Е₁, Е₂, … - некоторая последовательность испытаний (передач символов по каналу связи), пусть Т - событие символ будет передан по каналу связи правильно или нет в i -м испытании с вероятностью p_i или соответственно q_i = 1 - p_i. Тогда испытания называются независимыми по отношению к событию Т, если для любых непересекающихся множеств I, J испытаний вероятность того, что при Е_i Î I событие произойдет, а при Е_j Î J событие не произойдет равна .

Применяя формулу Бернулли для последовательности независимых испытаний, получаем теорему.

Теорема 4. Вероятность, что при передаче по двоичному симметричному каналу связи (p, q) слова длины n в нем произойдет k ошибок, равна

.(1)

Вероятность, что при передаче по двоичному симметричному каналу связи (p, q) слова длины n в нем произойдет не более k ошибок, равна

. (2)

Пример 2. Пусть p = 0,999. Тогда q = 0,001. Вероятность того, что при передаче слова длины 10 произойдет 0 ошибок равна (0,999)¹⁰ » 0,990; что произойдет 1 ошибка равна 10*(0,999)⁹(0,001) » 0,0099; что произойдет 2 ошибки равна 45*(0,999)⁸(0,001)² » 0,00005. Этот пример показывает, что наиболее вероятно в канале связи произойдет одна ошибка (из тысячи слов в среднем 10 слов придут с одной ошибкой). Эти одиночные ошибки необходимо обязательно необходимо обнаружить и исправить при декодировании.

В этой лекции рассмотрены методы увеличения надежности передачи информации с использованием систематических кодов, большая часть которых принадлежит к групповым кодам, основанным на использовании теоремы Лагранжа. Идея, положенная в основу этого метода состоит в том, что передаваемые слова кодируются более длинными словами тех же символов 0, 1. Приемник способен распознавать и исправлять ошибки, пользуясь дополнительной информацией, содержащейся в добавочных символах.

 

Блочные коды. Методика матричного кодирования.

Определение 1. Двоичным блочным (m,n)- кодом называется пара, состоящая из схемы кодирования (функции E: B^m ® Bⁿ) и схемы декодирования (функции D: Bⁿ ® B^m). Функции E и D выбираются таким образом, чтобы функция D° T°E, где T - функция ошибок, с вероятностью, близкой к единице, была тождественной. Таким образом математическую модель системы связи можно представить блок схемой (см. рис. 5).

Все коды делятся на два класса.

Коды с исправлением ошибок - имеют цель с вероятностью, близкой к единице, восстановить сообщение.

Коды с обнаружением ошибок - имеют цель с вероятностью, близкой к единице, выявить наличие ошибок.

Пример 1. Простой код с обнаружением ошибок, основан на проверке четности, и применим к любому сообщению a = a ₁ a ₂… a_m фиксированной длины. Это (m, m+ 1) - код.

Схема кодирования:

E: a = a ₁ a ₂… a_m ® b = b ₁ b ₂… b_{m +1}, где b_i = a_i, i = 1,..., ь,

. (2)

Например, E(1001)=10010, E(1011)=10111.

При кодировании сумма цифр любого кодового слова четная, если сумма цифр, принятого по каналу слова, нечетная, то приемник указывает наличие ошибок в сообщении, если четная, то предполагается, что в сообщении ошибок не произошло. Схема декодирования

E: b = b ₁ b ₂… b_{m +1}® g = с ₁ с ₂… с_m, где с_i = и_i, i = 1,..., m.

При кодировании с проверкой на четность будет обнаружена ошибка в полученном сообщении, если в нем произошло нечетное число ошибок в отдельных символах и не обнаружена ошибка в четном числе символов.

Вероятность не обнаружения ошибки в коде с проверкой на четность равна

. (1)

Пример 2. Простой код с исправлением ошибок, основанн на тройном повторении передаваемого слова a = a ₁ a ₂… a_m фиксированной длины. Это (m, 3 m) - код.

Схема кодирования:

E: a = a ₁ a ₂… a_m ® b = a ₁ a ₂… a_m a ₁ a ₂… a_m a ₁ a ₂… a_m

Например, E(1001)= 100110011001, E(1011)= 101110111011.

Схема декодирования. Принятое сообщение длины 3 m разбивается на блоки длины m. Если принятое сообщение состоит из трех одинаковых блоков длины, то считается, что оно пришло без ошибок, и декодируется принятым блоком. В общем случае в полученном блоке восстанавливается тот символ, который большее число раз встречается в тройке b_i b_{i+ 1}, b_{i +2} и ставится на i -е место в декодированном блоке (i = 1,..., m).

Например, для (4, 12) - кода D(101110010001) = 1001, D(001110110011)= 0011.

Вероятность того, что символ в данной позиции буде принят трижды правильно равна p ³, вероятность одной ошибки 3 p ³ q. Таким образом, вероятность принятия правильно символа в одной позиции p ³+3 p ³ q, вероятность ошибочного приема символа в одной позиции q ³+3 q ³ p.

Например, при p = 0,1 один символ будет принят неправильно с вероятностью 0,027. Это снижает вероятность ошибки на один символ с 10% до 2,8%. Отметим, что тройное повторение обеспечивает исправление одной ошибки за счет тройного увеличения времени передачи. Существуют (3,6) - коды, которые также исправляют одну ошибку, но только удваивая время передачи.

При блочных (m,n)-кодах передаваемые слова длины m кодируются кодовыми словами длины n (n > m). Для блочных (m,n)-кодов проблема оптимизации для кодов с исправлением ошибок состоит в следующем. При данных m и n найти такие Функции E и D, чтобы вероятность приема сигнала с ошибкой была минимальной. Например, для обнаружения одной ошибки минимальное расстояние между кодовыми словами должно равняться 2. Так как при расстоянии равном 1, одна ошибка переводит кодовое слово в другое, и оно не будет обнаружено.

Теорема 1. Для того чтобы код давал возможность обнаруживать все ошибки в не более чем k позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было равно k+ 1. Для такого кода вероятность того, что ошибка в сообщении не будет обнаружена, равна

.

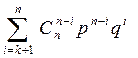Доказательство. Необходимость. Допустим, что код дает возможность обнаружить все ошибки в не более чем k позициях. Д окажем, что наименьшее расстояние между кодовыми словами было равно k+ 1. Допустим противное, что есть кодовые слова, расстояние между которыми меньше k+ 1. Тогда можно сделать в каждом из этих слов не более k ошибок и перевести одно слова в другое слово. Тогда ошибку нельзя обнаружить, так как неизвестно из которого слова оно произошло. Получаем противоречие.

Достаточность. Пусть наименьшее расстояние между кодовыми словами было равно k+ 1. Тогда обнаруживаем неверное слово по правилу. Если оно не совпадает с кодовым словом, то в нем произошла ошибка. При этом, если в кодовом слове сделать не более k ошибок, то ошибка будет обнаружена..

Теорема 2. Для того чтобы код давал возможность исправить все ошибки в не более чем k позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было равно 2 k+ 1.

Доказательство. Необходимость. Допустим, что код дает возможность исправить все ошибки в не более чем k позициях. Д окажем, что наименьшее расстояние между кодовыми словами было равно2 k+ 1. Допустим противное, что есть кодовые слова, расстояние между которыми меньше 2 k+ 1. Тогда можно сделать в каждом из слов не k более ошибок и перевести оба слова в одно слово. Тогда ошибку нельзя исправить, так как неизвестно из которого слова оно произошло. Получаем противоречие.

Достаточность. Пусть наименьшее расстояние между кодовыми словами было равно2 k+ 1. Тогда рассмотрим около каждого кодового слова шар радиуса k и декодируем все полученные сообщения по правилу: слово декодируем тем кодовым словом, которое находится от полученного слова на расстоянии не большем k, т.е. попадет в шар с центром в выбранном кодовом слове. При этом, если в кодовом слове сделать не более k ошибок, то оно будет восстановлено.

Для простого (1,3)-кода служит функция D; 000a0, 001a0, 010a0, 100a0, 011a0, 101a0, 110a0, 111a0, которая исправляет ошибки ровно в одной позиции.

С точки зрения групповой структуры удобно рассматривать строку ошибок. Работу канала связи можно объяснить следующим образом:

Данное сообщение a = a ₁ a ₂… a_m b = b ₁ b ₂… b_{m +1}перекодируется в кодовое слово b = b ₁ b ₂… b_n.

Канал связи добавляет в нему строку ошибок e = e ₁ e ₂… r_n. и приемник принимает сигнал r = r ₁ r ₂… r_n., где

r_i=b_i +e_i, i =1,2,… n.

Система, исправляющая ошибку, переводит слово r = r ₁ r ₂… r_n в ближайшее кодовое слово b = b ₁ b ₂… b_n, а система обнаруживающая ошибки, сигнализирует об ошибках.

Примеры 1. (2,3)-код с проверкой четности E; 00a000, 01a011, 10a100, 11a110. Ни одна из строк ошибок 001, 010, 100, 111 не переводит кодовое слов в кодовое слово. Поэтому все однократные и тройные ошибки будут обнаружены.

2. (2,5)-код с проверкой четности E; 00a00000, 01a01011, 10a10101, 11a11110. Эта система кодирования способна исправлять любые однократные ошибки, так как ближайшее кодовое расстояние между словами равно.

Кодирование таблицами, задающими кодовое слово для каждого блока, требует большого объема памяти. Поэтому используется, так называемая методика матричная кодирования, при которой запоминаются только коды m слов, имеющие по одной единице.

Пусть Е = (e_ij)- матрица размерности m ´ n, состоящая из нулей и единиц. Если знак "+" обозначает сложение по модулю 2, то схема кодирования определяется уравнениями:

. (2)

Последнее равенство можно записать матричным равенством:

b = a E. (3)

Преимущества матричного кодирования:

вместо 2 ^m требуется заполнить только m слов;

в первых m символах кодового слова стоит слово сообщение;

при получении кодовых слов необходимо только сложить по 2 только те строки матрицы, номера которых совпадают с номерами тех символов кода сообщения, которые равны 1.

Примеры 3. (3,6)-код задаем следующей матрицей

.

Полный список кодовых слов

000a000000, 001a100110, 010a010011, 100a001111, 011a110101, 101a101001, 110a011100, 111a111010.

 

Групповые коды. Таблица декодирования.

Определение 1. Блочный код называется групповым, если его кодовые слова образуют группу.

Теорема 1. Если код является групповым, то наименьшее расстояние между кодовыми словами равно наименьшему весу ненулевого кодового слова неравного нулю.

Доказательство. Пусть - кодовое слово наименьшего веса. Так как по теореме 4 параграфа 1 наименьшее расстояние d(a, b)между словамиd(a, b) = w(a - b) ³ w(m). Далее имеем w(m)= w(m - 0) = d(m, 0)³ d(a, b). Из полученных двух неравенств находим w(m) = d(a, b). 

Следствие 1. Для того чтобы групповой код давал возможность обнаруживать все ошибки в не более чем k позициях, необходимо и достаточно, чтобы наименьший вес кодового слова был равен k+ 1.

Следствие 2. Для того чтобы групповой код давал возможность исправлять все ошибки в не более чем k позициях, необходимо и достаточно, чтобы наименьший вес кодового слова был равен 2 k+ 1.

Теорема 2. Пусть Е - кодирующая m ´ n матрица, у которой есть единичная m ´ m подматрица. Тогда отображение aaa Е является мономорфизмом группы B^m сообщений в группу Bⁿ кодирующих слов.

Доказательство. Так как у кодирующей матрицы Е есть единичная подматрица, то кодовое слово, в которое кодируется слово a содержит всегда в качестве подслова слово a. Следовательно, указанное отображение переводит разные слова из B^m в различные кодовые слова из Bⁿ, и является инъекцией. Так как для любых слов сообщений a, a' имеем (a+ a') Е = a Е + a' Е, то указанное отображение является мономорфизмом. 

По теореме 2 образ группы при указанном отображении изоморфен группе и поэтому является подгруппой группы. Таким образом доказана теорема.

Теорема 3. Пусть Е - кодирующая m ´ n матрица, у которой есть единичная m ´ m подматрица. Тогда отображение aaa Е является групповым (m, n) - кодом. 

Примеры 3. (3,6)-код рассмотренный в примере 3 предыдущего параграфа является групповым кодом, в котором наименьший вес кодового слова равен 3 и код способен исправлять однократные ошибки и обнаруживать двойные.

Групповые коды не обнаруживают только такие ошибки, которые сами являются кодовыми словами, так как только при таких ошибках одни кодовые слова перейдут в другие кодовые слова. Вероятность, что ошибка не будет обнаружена равна сумме вероятностей всех строк ошибок, т.е. кодовых слов.

В примере 1 она равна 4 p ³ q ³ + 3 p ² q ⁴.

Схема декодирования группового кода. Разложим группу Bⁿ на классы смежности по подгруппе K кодовых слов:

Bⁿ = K È(K+ h₁) È(K+ h₂) È (K+ h₃) È …È(K+ h_s), s = 2 ^n-m -1

В каждом классе 2 ^m элементов. Пусть K = {0, b₁,b₂, …,b _r }, r = 2 ^m -1. В качестве представителя (лидера) h _i каждого класса K+ h _ш возьмем слово наименьшего веса в данном классе. Тогда каждый элемент из единственным образом представляется в виде суммы h _i + b _j лидера h _i соответствующего смежного класса и b _j Î K.

Теорема 4. В любом групповом коде, любой элемент x Î Bⁿ однозначно представляется в виде суммы x = b _j + h _k кодового слова b _j и лидера h _i.. 

Матрица декодирования содержит все элементы из Bⁿ и имеет вид

.

Декодирование полученного слова x = b _j + h _k состоит в выборе кодового слова b _j в качестве переданного и последующем применении операции E ^-1.

Пример 1. Рассмотрим (3,6) - код из примера 3 п.2 с матрицей кодирования

,

где совокупность кодовых слов 000a000000, 001a100110, 010a010011, 100a001111, 011a110101, 101a101001, 110a011100, 111a111010.

Таблица декодирования

Строка кодовых слова®
Столбец лидеров

Чтобы декодирование принятое слово x = b _j + h _k следует отыскать его в таблице декодирования и выбрать в качестве передаваемого слова кодового слова b _j в том же столбце, но в первой строке. Затем слово b _j декодировать.

Например, если принято слово 010010, то считается что передано слово 010011 и при передач произошла ошибка в шестом символе. Далее слово дешифруется словом 010.

Теорема 5. Групповое кодирование посредством лидеров справляет в точности те строки ошибок, которые являются лидерами.

Вероятность правильного декодирования, переданного по двоичному симметричному каналу слова равна сумме вероятностей всех лидеров, включая нулевой. В нашем примере для слова длины 6 вероятность правильного декодирования равна p ⁶ + 6 p ⁵ q + p ⁴ q ².

Теорема 6. Если все лидеры является словами наименьшего веса в своем классе, то кодовое слово, стоящее в данном столбце, является ближайшим кодовым словом ко всем словам этого столбца.

Доказательство. Пусть мы передали слово b _j и приняли слово b _j + e _j. Расстояние от b _j до b _j +e _j равно w(e _j). Расстояние от до любого другого кодового слова равно весу разности этих слов, которая лежит в том же смежном классе, что и b _j. Поэтому этот вес не меньше веса лидера.

Последняя теорема означает, что такой выбор оптимален, так как минимизирует вероятность ошибки при передаче по двоичному симметричному каналу.

Групповой код не обнаруживает и не исправляет в точности те ошибки, которые совпадают с кодовыми словами. Поэтому вероятность не обнаружения ошибки при групповом кодировании равна вероятности появления ошибок равных кодовым ненулевым словам. В нашем примере вероятность равна 4 p ³ q ³ + 3 p ² q ⁴ .

Геометрическая интерпретация. Кодирующая схема двоичного (m,n)- кода определяет инъекцию множества B^m сигналов длины m в гиперкуб Bⁿ. В графе, вершины которого являются вершинами гиперкуба, а ребра его ребрами, расстояние между вершинами совпадает с расстоянием между соответствующими словами.

Схема декодирования отображает Bⁿ в B^m, так что прообраз каждого слова длины m состоит в точности из тех словиз Bⁿ, которые будут декодированы данным словом. Чтобы кодирование исправило все ошибки веса £ w, каждый такой класс эквивалентности должен содержать шар радиуса w с центром E (a), состоящий из слов, расстояние которых от кодового слова не больше w. Таких слов имеется

Код называется совершенным, если все классы эквивалентности являются такими шарами

Чтобы блочный (m,n) - код был совершенным, необходимо выполнение условия =2^n-m

Коды Хэмминга.

Опишем процедуру построения (m, m+r) кода Хемминга.

1) Выберем целое положительное число r из условия 2 ^{r- 1} - 1< m+r £ 2 ^r- 1, 2 ^{r- 1} - 1- r < m £ 2 ^r- 1- r. Можно всегда считать m = 2 ^{r- 1} - 1- r, n = 2 ^{r- 1} - 1. Сообщениями будут слова длины m, а кодовые слова длины m+r.

Например, при (m, m+ 4) -кода Хемминга имеем 2^{4 - 1} - 1- 4 < m £ 2⁴ - 1-4, 3 < m £ 11.

2) В каждом кодовом слове b = b ₁ b ₂ … b_n имеется r контрольных символов, это символы номера которых есть степени числа 2, т.е. символы . Остальные стальные m символов в естественном порядке - символы сообщения.

Например, для (10, 14) кода Хемминга при символы - контрольные, а - символы сообщения.

3) Построим матрицу M из m+r строк и r столбцов. В i -й строке матрицы M стоят символы двоичного разложения числа i.

Например, для (1,3)-кода, (4,7)-кода, (9,13)-кода, (11,15)-кода Хемминга эти матрицы имеют соответственно вид:

 

 

4) Запишем систему уравнений b M =0, где M - матрица, указанная выше. Она состоит из r уравнений. Контрольный символ находятся сложением по модулю 2 тех символов b_k кодируемого слова, для которых в i - столбце и k -й строке и матрицы М стоит единица.

Например, для (4,7)-кода система уравнений имеет вид:

5) Чтобы закодировать сигнал, возьмем в качестве b_k, k ¹2 ^j, соответствующие символы кодируемого слова и отыщем (i = 1, 2, 4, …, r -1) из написанной системы уравнений Так как в каждое из уравнений входит ровно одно , то это сделать нетрудно. В написанной системе b ₄, входит в первое уравнение, b ₂ - во второе, b ₁ - в третье.

Наименьший ненулевой вес кодового слова равен 3.

Декодирование. Пусть принято слово x = b+ e, где b - переданное слово, e - строка ошибок. Так как b M =0, то (b+ e) M = b M + e M = 0 + e M = e M. Если результат нулевой, как происходит при правильном приеме, то считается, что ошибок нет. Если вектор ошибок имеет единицу в i -й позиции, , то при умножении e на M получается i -я строка матрицы, т. е. двоичное разложение числа i. Тогда следует изменить в принятом слове символ в i -й позиции слова.

Пример 1. Рассмотрим (4, 7) - код Хемминга. Матрица М = М _7,3 которого имеет вид

Возьмем слово сообщение a = 0111. Решая указанную выше систему находим слово сообщение b = 0001111.

Имеем b M =0. Добавим к b строку ошибок e = 0000100. Тогда b+ e = 0001011 и (b+ e) М = 101. Это двоичное представление числа 5, так что ошибка находится в 5-й позиции. Если e = 0000001, то (b+ e) М = 111, т.е. 7 в двоичной записи, поэтому в 7-й позиции ошибка.

Если ошибка допущена более чем водной позиции, декодирование даст неверный результат. Например, если строка ошибок e будет кодовой, то (b+ e) М = 0, и декодирование не изменит принятого слова. Если ошибка допущена в двух позициях, код укажет позицию, но неправильно. Например, если e = 0000101, то (b+ e) М = 010, т.е. 2 в двоичной записи, поэтому во 2-й позиции ошибка. Последнее неверно.

Если к этому коду добавить проверку четности, то получим код наименьшего веса 4, способный устранять ошибку в одной позиции и обнаруживать ошибки в двух позициях.

Отметим, что коды Хемминга совершенные, минимальное кодовое расстояние в коде Хемминга равно 3 и они исправляют все одинарные ошибки и ни каких других ошибок они не исправляют. В таблице декодирования у такого кода будет 0 и все m строки ошибок ровно с одной единицей. В обще случае совершенный код исправляющий все ошибки в не более чем k позициях должен иметь лидерами все строки веса не более чем k, т.е. с не более чем k единицами.