Отношение сравнимости по модулю в кольце целых чисел и его свойства

ПАМ

Толстиков А.В.

Лекция 4. Теория сравнений для кольца целых чисел.

 

1. Отношение сравнимости по модулюв кольце целых чисел и его свойства.

2. Классы вычетов по модулю и их свойства.

3. Функция Эйлера. Теоремы Эйлера и Ферма.

4. Сравнения с неизвестным. Сравнения первой степени с одним неизвестным.

5. Системы линейных сравнений по модулю. Китайская теорема об остатках.

6. Сравнения n -й степенипо простому и по составному модулю.

Литература. Виноградов И.М. – С. 369-395;

Василенко О.Н. –С. 254- 273;

Коробейников А. Г. и др. –С. 2-17

Молдовян Н.А., Молдовян А.А. Введение в криптосистемы с открытым ключом: Учебное пособие. –СПб.: БХВ-Петербург, 2005.

Отношение сравнимости по модулю в кольце целых чисел и его свойства

Определение 1. Целые числа а и b называются сравнимыми по модулю натурального числа m, если m делит разность a-b.

Обозначается a º b (mod m).

Например, 31º 52(mod 7), 31T 21(mod 7).

Отношение сравнимости по модулю обладает следующими свойствами.

Теорема 1. Два целых числа а и b сравнимы по модулю m тогда и только тогда, когда остатки от деления чисел a и b на число m равны.

Доказательство. Разделим числа a и b на число m с остатком:

a = mq ₁ +r ₁, 0 £ r ₁ < m; b = mq ₂ +r ₂, 0 £ r ₂ < m. (1)

Пусть a º b (mod m). Тогда по определению 1 m делит

a-b = mq ₁ +r ₁ - mq ₂ +r ₂ = m (q ₁ - q ₂) + (r ₁ -r ₂).

Тогда по свойствам делимости m делит r ₁ -r ₂. Так как - m < r ₁- r ₂ < m, т.е. | r ₁- r ₂|< m, то по свойству делимости r ₁ -r ₂ = 0 и r ₁ = r ₂.

Обратно, пусть r ₁ = r ₂. Тогда из (1) получаем

a-b = mq ₁ +r ₁ - mq ₂ +r ₂ = m (q ₁ - q ₂).

Отсюда по определению 1 a º b (mod m).ÿ

Согласно этой теореме сравнимые числа по модулю еще называют равноостаточными.

Теорема 2. Отношение сравнимости целых чисел по модулю есть отношение эквивалентности, т.е. оно

1) рефлексивно, (" a Î Z)[ a º a (mod m)];

2) симметрично, (" a, b Î Z)[ a º b (mod m) Þ b º a (mod m)];

3) транзитивно, (" a, b, c Î Z)[ a º b (mod m) & b º c (mod m)Þ a º c (mod m)].

Доказательство. Утверждения теоремы следуют из свойств делимости целых чисел. Например, докажем свойство 3. Пусть a º b (mod m) и b º c (mod m). По определению 1 имеем m |(a-b) и m |(b-c). Тогда по свойству делимости m делит (a-b)+(b-c) = a-c. Следовательно, a º c (mod m). ÿ

Теорема 3. Для любых целых чисел a, b, c, d и n Î N справедливы свойства:

1) a º b (mod m) & c º d (mod m) Þ a+ c º b+ d (mod m);

2) a º b (mod m) & c º d (mod m) Þ a- c º b- d (mod m);

3) a º b (mod m) & c º d (mod m) Þ ac º bd (mod m);

4) a º b (mod m) Þ ac º bc (mod m);

5) a º b (mod m) Þ aⁿ º bⁿ (mod m).

Доказательство. Утверждения теоремы следуют из свойств делимости целых чисел. Например, докажем свойство 3. Пусть a º b (mod m) и c º d (mod m). По определению 1 имеем m |(a-b) и m |(c-d). Тогда по свойству делимости m делит c (a-b)+ b (с-d) = ca - bd. Следовательно, ac º bd (mod m). ÿ

Следствие 1. Для любого многочлена f (x) = a ₀ xⁿ + a ₁ x^{n- 1}+…+ a_n Î Z [ x ] и для любых целых чисел a, b, если a º b (mod m), то f (a) º f (b) (mod m).

Определение 2. Два целочисленных вектора a = (a ₁, a ₂,…, a_n)и b = (b ₁, b ₂,…, b_n) называются сравнимыми по модулю натурального числа m, если все соответствующие координаты векторов сравнимы по модулю m.

Обозначаем a º b (mod m).

Следствие 2. Для любого многочлена f (x)Î Z [ x ] и для любых целочисленных векторов a, b, если a º b (mod m), то f (a) º f (b) (mod m), x = (x ₁, x ₂,…, x_n)

Теорема 4. Для любых целых чисел a, b, d > 0 справедливы свойства:

1) a º b (mod m) Û ad º bd (mod md);

2) ad º bd (mod m), (d, m) = 1 Þ a º b (mod m);

Доказательство. Утверждения теоремы следуют из свойств делимости целых чисел. Например, докажем свойство 2. Пусть ad º bd (mod m), (d, m) = 1. По определению 1 имеем m |(ad - bd). Тогда m |(a – b) d, где (d, m) = 1. Отсюда по свойству взаимно простых чисел получаем m |(a – b). Следовательно, a º b (mod m). ÿ

2. Классы вычетов по модулю и их свойства

Определение 1. Классом вычетов числа a по модулю m называется множество всех целых чисел, сравнимых с числом a по модулю m.

Класс вычетов числа по модулю m обозначается символом или просто , если известно о каком модуле идет речь. Множество всех классов вычетов по модулю обозначается символом Z _m.

Из свойств сравнений следуют следующие свойства классов вычетов.

1⁰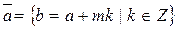

2⁰ a Î , и ¹Æ.

3⁰ 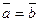Û a º b (mod m).

4⁰ Любые два класса вычетов либо совпадают, либо их пересечение пусто.

5⁰ Всего имеется m классов вычетов по модулю m и все классы вычетов по модулю m исчерпываются классами .

Свойство 4⁰ следует из того, что каждое целое число сравнимо с одним из чисел 0, 1, 2,…, m -1 и эти числа попарно не сравнимы по модулю m (см. теорему 1 параграфа 1).

Определение 2. Суммой и произведением классов вычетов по модулю m называются соответственно классы и .

Из определения группы и кольца и свойств сравнений получаем теоремы.

Теорема 1. Множество Z _m всех классов вычетов по модулю m образует аддитивную абелеву группу порядка m относительно операции сложения классов вычетов.

Теорема 2. Множество Z _m всех классов вычетов по модулю m образует конечное коммутативное кольцо с единицей относительно операций сложения и умножения классов вычетов.

Если из каждого класса вычетов по модулю m взять ровно по одному числу, то получим множество, состоящее из m чисел, которое называется полной системой вычетов по модулю m.

Например, полными системами вычетов по модулю m = 6являются множества

{0, 1, 2, 3, 4, 5}, {1, 2, 3,4, 5, 6}, {-2, -1, 0, 1, 2, 3}, {-5, -4, -3, -2,-1, 0}.

Можно составить бесконечное число полных систем вычетов по модулю m, но все они обладают двумя свойствами:

1) каждая полная система вычетов содержит m чисел;

2) числа полной системы вычетов попарно несравнимы по модулю m.

Эти свойства являются характеристическими. Т.е. справедлива теорема

Теорема 3. Любые m попарно несравнимых по модулю m чисел a ₁, a ₂,…, a_m образуют полную систему вычетов по модулю m.

Доказательство. Так как числа a ₁, a ₂,…, a_m попарно несравнимы по модулю m, то классы ` a <sub>1</sub>, ` a ₂,…, ` a<sub>m</sub> попарно различны и образуют множество Z <sub>m</sub> всех классов вычетов по модулю m. Так как числа a <sub>1</sub>, a <sub>2</sub>,…, a<sub>m</sub> принадлежат соответственно классам ` a ₁, ` a <sub>2</sub>,…, ` a_m, то эти числа образуют полную систему классов вычетов по модулю m. ÿ

Теорема 4. Пусть a и b целые числа и (a, m) = 1. Тогда, если переменная x пробегает полную систему вычетов по модулю m, то значения линейной функции ax + b пробегают полную систему вычетов по модулю m.

Доказательство. Пусть числа a ₁, a ₂,…, a_m образуют полную систему вычетов по модулю m. Покажем, что числа

aa ₁ + b, aa ₂ + b,…, aa_m + b (1)

образуют полную систему вычетов по модулю m. В силу теоремы 1 достаточно доказать, что числа (1) попарно несравнимы по модулю m. Допустим противное, что

aa_i + b º aa_j + b (mod m)., i ¹ j.

Отсюда, применяя свойства сравнений, и используя условие (a, m) = 1, последовательно получаем

aa_i º aa_j (mod m), a_i º a_j (mod m)

противоречие.ÿ

Определение 3. Классом вычетов числа a по модулю m называется примитивным, если (a, m) = 1.

Множество всех примитивных классов вычетов по модулю m обозначается через Z _m ´.

Лемма 1. Любой примитивный класс вычетов по модулю m состоит из чисел взаимно простых с m.

Доказательство. Пусть примитивный класс вычетов по модулю m. Тогда (a, m) = 1. Пусть b Î . Тогда b = a + mq, q Î Z. По свойству НОД

НОД(b, m) = НОД(a + mq, m) = = НОД(a, m) = 1.ÿ

Определение 4. Функцией Эйлера j(m) называется функция, определенная на множестве N натуральных чисел, такая что для любого m Î N j(m) обозначает количество натуральных чисел взаимно простых с m ине превосходящих m.

Например, j(2) = 1, j(3) = 2, j(4) = 2, j(5) = 4, j(6) = 2.

Так как все классы вычетов совпадают с классами , то число примитивных классов вычетов равно, количеству чисел из множества {0, 1, 2,…, m -1}, взаимно простых с m, т.е. равно j(m).

Если из каждого примитивного класса вычетов по модулю m взять ровно по одному числу, то получим множество, состоящее из j(m) чисел, которое называется приведенной системой вычетов по модулю m.

Например, приведенными системами вычетов по модулю m = 6являются множества

{1, 5}, {-1, 1}, {-5, -1}.

Можно составить бесконечное число приведенных систем вычетов по модулю m, но все они обладают тремя свойствами:

1) каждая приведенная система вычетов содержит j(m) чисел;

2) числа приведенной системы вычетов попарно несравнимы по модулю m.

3) числа приведенной системы вычетов взаимно просты с m.

Эти свойства являются характеристическими. Т.е. справедлива теорема

Теорема 5. Любые j(m) попарно несравнимых по модулю m и взаимно простых с m чисел a ₁, a ₂,…, a _{j( m )} образуют приведенную систему вычетов по модулю m.

Доказательство. Так как числа a ₁, a ₂,…, a _{j( m )}попарно несравнимы по модулю m, и взаимно просты с m, то классы ` a <sub>1</sub>, ` a ₂,…, ` a <sub>j( m )</sub> попарно различны, примитивные и образуют множество Z <sub>m</sub> ´ всех примитивных классов вычетов по модулю m. Так как числа a <sub>1</sub>, a <sub>2</sub>,…, a <sub>j( m )</sub>принадлежат соответственно классам ` a ₁, ` a <sub>2</sub>,…, ` a _{j( m )}, то эти числа образуют приведенную систему классов вычетов по модулю m. ÿ

Теорема 6. Пусть a - целое число и (a, m) = 1. Тогда, если переменная x пробегает приведенную систему вычетов по модулю m, то значения линейной функции ax пробегают приведенную систему вычетов по модулю m.

Доказательство. Пусть числа a ₁, a ₂,…, a _{j( m )}образуют приведенную систему вычетов по модулю m. Покажем, что числа

aa ₁, aa ₂ ,…, aa _{j( m )} (2)

образуют приведенную систему классов вычетов по модулю m. Так как (a, m) = 1, и (a_i, m) = 1, то по свойству взаимно простых чисел, числа множества (2) взаимно просты с числом m. В силу теоремы 5 достаточно доказать, что числа (2) попарно несравнимы по модулю m. Допустим противное, что

aa_i º aa_j (mod m)., i ¹ j.

Отсюда, применяя свойства сравнений, и используя условие (a, m) = 1, последовательно получаем

a_i º a_j (mod m)

противоречие.ÿ

Теорема 7. Множество Z _m ´ всех примитивных классов вычетов по модулю m образует абелеву мультипликативную группу порядка j(m) относительно операции умножения классов вычетов.

Доказательство Так как , то . Пусть ` a, ` b - примитивные классы вычетов по модулю m. Тогда по определению (a, m) = 1, (b, m) = 1 и по свойству взаимно простых чисел (ab, m) = 1. Тогда класс вычетов - примитивный. Так как операция умножения классов вычетов однозначна, то отсюда получаем, что операция умножения на является бинарной алгебраической операцией. Проверим аксиомы группы.

1. .

2. .

3. Пусть все примитивные классы вычетов по модулю m. Пусть ` a - примитивный класс. Тогда классы

(3)

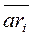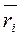- примитивные по модулю m. Покажем, что они попарно различны. Допустим противное, что для некоторых i, j, i¹ j, имеем . Тогда и по определению равенства классов получим . Так как (a, m) = 1, то по свойству сравнений выводим . Последнее противоречит тому, что классы различные. Следовательно, множество (1) равно . Поэтому в (1) найдется такой класс равный `1, . Таким образом, класс является обратным для класса ` a.

4. ÿ

Из доказанной теоремы получаем следующую теорему.

Теорема 8. Множество Z _m всех классов вычетов по модулю m образует поле тогда и только тогда, когда m – простое число.