Зависимыми (связными) называют выборки, если процедура эксперимента и полученные результаты измерения некоторого свойства, проведенные по одной выборке, оказывают влияние на другую.
· Следует определить однородность – неоднородность выборки.
Однородность выборки означает, что психолог, изучая, например, подростков не может включать в исследование взрослых людей. Основаниями для формирования однородной выборки могут служить следующие характеристики: пол, возраст, уровень интеллекта, национальность, отсутствие определенных заболеваний и т. д.
· Затем следует оценить объем выборки и, зная ограничения каждого критерия по объему, выбрать соответствующий критерий.
· При этом целесообразнее всего начинать работу с выбора наименее трудоемкого критерия.
· Если используемый критерий не выявил различия – следует применить более мощный, но одновременно и более трудоемкий критерий.
· Если имеется несколько критериев, то следует выбирать те из них, которые наиболее полно используют информацию, содержащуюся в экспериментальных данных.
8.3. Непараметрические критерии для связных выборок.
Парный критерий Т – Вилкоксона
Для решения задач, в которых осуществляется сравнение двух рядов чисел психолог может использовать парный критерий Т - Вилкоксона. Этот критерий применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, т. е. он позволяет установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом.
Критерий Т основан на ранжировании абсолютных величин разности между двумя рядами выборочных значений в первом и втором эксперименте (например, до и после какого-либо воздействия). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем наряду с общей суммой рангов находится отдельно сумма рангов, как для положительных, так и для отрицательных сдвигов. Если интенсивность сдвига в одном направлении оказывается большей, то и соответствующая сумма рангов также оказывается больше. Этот сдвиг называется типичным, а противоположный, меньший по сумме рангов сдвиг – нетипичным. Эти два сдвига оказываются дополнительными друг другу. Критерий Т - Вилкоксона базируется на величине нетипичного сдвига, который называется Т 
Пример: Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений.
Для решения этой задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В табл. 5 приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т - Вилкоксона.
Таблица 5
| № испытуемых п/п | До коррек ционной работы | После коррек ционной работы | Сдвиг (значение разности с учетом знака) | Абсолютные величины разностей | Ранги абсолютных величин разностей | Символ нетипичного двига |
| -2 | 10,5 | |||||
| -1 | 6,5 | |||||
| +1 | 6,5 | * | ||||
| -8 | ||||||
| -11 | ||||||
| -20 | ||||||
| -18 | ||||||
| -1 | 6,5 | |||||
| +1 | 6,5 | * | ||||
| -22 | ||||||
| -1 | 6,5 | |||||
| -2 | 10,5 | |||||
| -6 | 13,5 | |||||
| -4 | ||||||
| -1 | 6,5 | |||||
| +6 | 13,5 | * | ||||
| Сумма | Т = 26,5
|
Обработка данных по критерию Т – Вилкоксона осуществляется следующим образом:
1. В четвертый столбец таблицы вносятся величины сдвигов с учетом знака. Их вычисляют путем вычитания из чисел третьего столбца соответствующих чисел второго столбца.
2. В пятом столбце в соответствие каждому значению сдвига ставят его абсолютную величину.
3. В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце.
4. По формуле: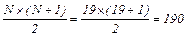 
подсчитывают сумму рангов. В нашем примере она составляет:
12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + 10,5 + 13,5 + 12 + 6,5 + 13,5 +2 = 190
5. Проверяют правильность ранжирования на основе совпадения сумм рангов полученных двумя способами. В нашем случаи обе величины совпали, 190 = 190, следовательно, ранжирование проведено правильно.
6. Любым символом отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае это три положительных сдвига.
7. Суммируют ранги нетипичных сдвигов. Это и будет искомая величина Т . В нашем случае эта сумма равна: Т = 6,5 + 13,5 + 6,5 = 26,5.
По табл. 15 приложения 6 определяют критические значения Т 
для n = 19.
Нужная нам строка табл. 15 из приложения 6 выделена ниже в табл. 7.
Таблица 6
| n | P | |
| 0,05 | 0,01 | |
Поскольку в нашем случаи основной, типичный сдвиг – отрицательный, то дополнительный, «нетипичный» сдвиг будет положительным и на уровне значимости в 5% сумма рангов таких сдвигов не должна превышать числа 53, а при уровне значимости в 1% не должна превышать числа 38. Представим сказанное выше следующим образом:
Т = 53 для P 
0,05
38 для P 0,01 
Строим «ось значимости»:
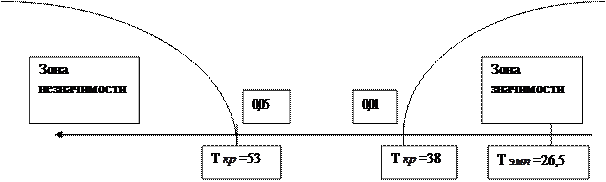
Анализ «оси значимости» показывает, что полученная величина Т попадает в зону значимости. Следовательно, можно утверждать, что зафиксированные в эксперименте изменения не случайны и значимы на 1% уровне. Таким образом, психолог может говорить о том, что применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы, следовательно, оказывает положительное влияние на развитие внимания школьников.
Для применения критерия Т – Вилкоксона необходимо соблюдать следующие условия:
1. Измерение может быть проведено во всех шкалах, кроме номинальной.
2. Выборка должна быть связной.
3. Число элементов в сравниваемых выборках должно быть равным.
4. Критерий Т - Вилкоксона может применяться при численности выборки от 5 до 50 (на большую величину не рассчитана таблица достоверности).
8.4. Непараметрические критерии для несвязных выборок.
Критерий U Вилкоксона – Манна – Уитни
Несвязанные или независимые выборки образуются, когда в целях эксперимента для сравнения привлекаются данные двух или более выборок, причем эти выборки могут быть взяты из разных генеральных совокупностей. Таким образом, для несвязанных выборок характерно, что в них обязательно входят разные испытуемые.
Для оценки достоверности различий между несвязными выборками используется ряд непараметрических критериев. Одним из наиболее распространенных является критерий U. Этот критерий применяют для оценки различий по уровню выраженности какого-либо признака для двух независимых (несвязных) выборок. При этом выборки могут различаться по числу входящих в них испытуемых. Этот критерий особенно удобен в том случае, когда число испытуемых невелико и в обеих выборках не превышает число 20, хотя таблицы критических значений рассчитаны для величин выборок, не превышающих 60 человек испытуемых.
Пример: Две неравные по численности группы испытуемых решали техническую задачу. Показателем успешности служило время решения. Испытуемые меньшей по численности группы получали дополнительную мотивацию в виде денежного вознаграждения. Психолога интересует вопрос – влияет ли вознаграждение на успешность решения задачи?
Психологом были получены следующие результаты времени решения технической задачи в секундах: в первой группе – с дополнительной мотивацией – 39, 38, 44, 6, 25, 25, 30, 43; во второй группе – без дополнительной мотивации – 46, 8, 50, 45, 32, 41, 41, 31, 55. Число испытуемых в впервой группе обозначается как n1 и равно 8, во - второй как n2 и равно 9.
Для ответа на вопрос задачи применим критерий U Вилкоксона – Манна – Уитни. Существует два способа подсчета по критерию U. Мы рассмотрим (первый) наиболее
простой способ.
Полученные данные необходимо объединить, т. е. представить как один ряд и упорядочить его по возрастанию входящих в него величин. Подчеркнем, что для критерия U важны не сами численные значения данных, а порядок их расположения. Предварительно обозначим каждый элемент первой группы символом х, а второй - символом у. Тогда общий упорядоченный по возрастанию численных величин ряд можно представить так:
x y x x x y y x x y y x x y y y y Модифицированный ряд
6 8 25 25 30 31 32 38 39 41 41 43 44 45 46 50 55
Если бы упорядоченный ряд, составленный по данным двух выборок, принял бы такой вид:
x x x x x x x x x y y y y y y y y y y y y
то, очевидно, что такие две выборки значимо различались бы между собой, такое расположение называется идеальным. Критерий U основан на подсчете нарушений в расположении чисел в упорядоченном экспериментальном ряду по сравнению с идеальным рядом. Любое нарушение порядка идеального ряда называют инверсией. Одним нарушением (одной инверсией) считают такое расположение чисел, когда перед некоторым числом первого ряда, стоит только одно число второго ряда. Если перед некоторым числом первого ряда стоит два числа второго ряда, то возникают две инверсии и т. д.
Удобно подсчитывать число инверсий, расположив исходные данные в виде таблицы, в которой один столбец состоит из данных первого ряда, а второй из данных второго. При этом и первый и второй столбцы имеют пропуски чисел, которые обозначаются символом «-».
Пропуск в первом столбце означает, что в соседнем столбце имеется число, занимающее промежуточное положение по отношению к числам первого столбца, ограничивающим пропуск. То же самое верно для пропусков второго столбца. Упорядоченное объединение экспериментальных данных в порядке их возрастания, представленное отдельно в первом и втором столбце с учетом пропусков и является по существу модифицированным рядом. Представим этот модифицированный ряд в виде табл. 6, в которую добавлены еще два столбца для подсчета инверсий. В третьем столбце таблицы даны инверсии первого столбца по отношению ко второму, они обозначаются как инверсии X/Y, а четвертом столбце инверсии второго столбца по отношению к первому, они обозначаются как инверсии Y/X.
Таблица 7
| Группа с дополнительной мотивацией X | Группа без дополнительной мотивации Y | Инверсии X/Y | Инверсии Y/X |
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| Суммы инверсий |
Инверсии X/Y подсчитываются следующим образом: число 6 первого столбца не имеет перед собой никаких чисел второго столбца, поэтому в третьем столбце напротив числа 6 ставим ноль; числа 25, 25 и 30 первого столбца (х) имеют перед собой только одно число второго столбца – 8 (у), т. е. имеют по одной инверсии, поэтому в столбце 3 для инверсий X/Y каждому из чисел 25, 25 и 30 ставим в соответствие число 1. Числа 38 и 39 первого столбца имеют перед собой по три числа второго столбца – это числа 8, 31 и 32, т. е. имеют по три инверсии. Последние два числа первого столбца 43 и 44 имеют перед собой пять чисел второго столбца, т. е. по 5 инверсий. Таким образом, суммарное число инверсий X/Y третьего столбца составляет:
U (x/y) = 1 + 1 + 1 + 3 + 3 + 5 + 5 =19
Необходимо рассчитать также число инверсий второго столбца (y) по отношению к первому (x), т. е. суммарное число инверсий Y/X. Поскольку число 8 (y) имеет перед собой одно число первого столбца – 6, то столбце 4 с инверсиями для Y/X напротив числа 8 ставим число инверсий -1; числа 31 и 32 второго столбца имеют перед собой четыре числа первого столбца: 6, 25, 25 и 30, следовательно, числу 31 и числу 32 приписываем в столбце 4 величины инверсий равные 4, и так далее. Таким образом, суммарное число инверсий Y/X четвертого столбца составляет:
U (x/y) = 1 + 4 + 4 + 6 + 6 + 8 + 8 +8 + 8 = 53
Видно, что во втором случае сумма инверсий существенно больше. Принято считать, что U есть минимальное из сумм инверсий.
Или, иначе говоря, U = min (U(x/y), U(y/x)) = 19
Получив U обращаемся к табл. 16 приложения 6. Эта таблица состоит из нескольких таблиц, рассчитанных отдельно для уровней P = 0,05, P = 0,01, а также для величин n1 и n2. В нашем случае n1 = 8 и n2 = 9. По этим таблицам находим, что значения U 
равны:
18 для P 
0,05
11 для P 0,01
Соответствующая «ось значимости» имеет вид:
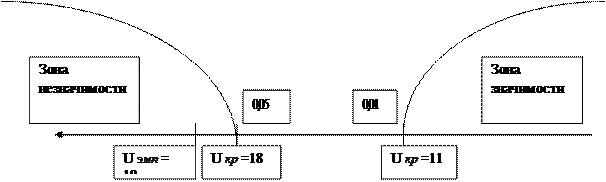
Полученное значение U попало в зону незначимости, следовательно, принимается гипотеза H 
о сходстве, а гипотеза H 
о наличии различий отклоняется. Таким образом, психолог может утверждать, что дополнительная мотивация не приводит к статистически значимому увеличению эффективности решения технической задачи.
Для применения критерия U необходимо соблюдать следующие условия:
1. Измерение должно быть произведено в шкале интервалов и отношений.
2. Выборки должны быть несвязанными.
3. Нижняя граница применимости критерия n1 
3 и n2 3 или n1 = 2, а n2 5.
4. Верхняя граница применимости критерия: n1 и n2 60
8.5. Параметрические критерии различия
Критерии носят название «параметрические », потому, что в формулу их расчета включаются такие параметры выборки, как среднее, дисперсия и др. Как правило, в психологических исследованиях чаще всего применяются два параметрических критерия – это t - критерий Стьюдента, который оценивает различия средних для двух выборок и F - критерий Фишера, оценивающий различия между двумя дисперсиями.
8.5.1. Т - Критерий Стьюдента
Критерий t Стьюдента направлен на оценку различий величин средних 
и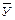 
двух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.
Случай несвязных выборок
В общем случае формула для расчета по t - критерию Стьюдента такова:
t = 
где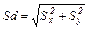 
Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n,тогда выражение (9.2) будет вычисляться следующим образом:
В случае неравночисленных выборок n1 
n2, выражение будет вычисляться следующим образом:
|
| Sd = |
В обоих случаях подсчет числа степеней свободы осуществляется по формуле:
к = (n1 - 1) + (n2 - 1) = n1 + n2 - 2
где n1 и n2 соответственно величины первой и второй выборки.
Понятно, что при численном равенстве выборок k = 2 
n - 2.
Рассмотрим пример использования t - критерия Стьюдента для несвязных и неравных по численности выборок.
Пример: Психолог измерял время сложной сенсомоторной реакции выбора
(в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X)входили 9 спортсменов высокой квалификации. Контрольной группой (Y)являлись 8 человек, активно не занимающихся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.
Результаты эксперимента представим в виде табл. 9, в которой произведем ряд необходимых расчетов:
Таблица 8
| № | Группы | Отклонение от среднего | Квадраты отклонения | |||
| X | Y | 
| 
| 
| 
| |
| - 22 | - 58 | |||||
| - 106 | ||||||
| - 17 | ||||||
| - 2 | ||||||
| - 77 | ||||||
| - 36 | ||||||
| - 8 | ||||||
| - | - 56 | - | - | |||
| Сумма | ||||||
| Среднее |
Средние арифметические составляют в экспериментальной группе 
, в контрольной группе 
Разница по абсолютной величине между средними
| - 
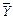| = 526 - 638 = 112.
Подсчет выражения дает:
Sd = 
Тогда значение t , вычисляемое по формуле (9.1), таково:
t = 
Число степеней свободы k = 9 + 8-2= 15. По табл. 17 приложения 6для данного числа степенейсвободы находим t 
:
2,13 для P 0,05
2,95 для P 0,01
4,07 для P 0,001
Строим «ось значимости»:
Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,]% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом.
В терминах статистических гипотез это утверждение звучит так: гипотеза Hо о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза H1 - о различии между экспериментальной и контрольными группами.
Случай связных выборок
В случае связных выборок с равным числом измерений в каждой можно использовать более простую формулу t - критерия Стьюдента.
Вычисления значений t осуществляется по формуле:
t = 
= 
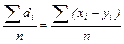
где 
- разности между соответствующими значениями переменной X и переменной Y, а среднее этих разностей.
В свою очередь 
вычисляется по следующей формуле:
Число степеней свободы k определяется по формуле k = n – 1
Рассмотрим пример использования t - критерия Стьюдента для связных и, очевидно, равных по численности выборок.
Пример: Психолог предположил, что в результате научения время решения эквивалентных задач «игры в 5» (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач. Решение задачи представим в виде табл. 10.
Таблица 9
| № испытуемых | 1 задача | 2 задача |
| 
|
| 4,0 | 3,0 | 1,0 | 1,0 | |
| 3,5 | 3,0 | 0,5 | 0,25 | |
| 4,1 | 3,8 | 0,3 | 0,09 | |
| 5,5 | 2,1 | 3,4 | 11,56 | |
| 4,6 | 4,9 | -0,3 | 0,09 | |
| 6,0 | 5,3 | 0,7 | 0,49 | |
| 5,1 | 3,1 | 2,0 | 4,00 | |
| 4,3 | 2,7 | 1,6 | 2,56 | |
| Суммы | 37,1 | 27,9 | 9,2 | 20,04 |
Вначале произведем расчет по формуле:
Затем применим формулу:
И, наконец, следует применить формулу. Получим:
t 
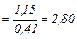
Число степеней свободы: k = 8 – 1 = 7 и по табл. 17 приложения 6 находим t :
2,37 для P 0,05
З,50 для P 0,01
5,41 для P 0,001
Строим «ось значимости»:
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее время решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Ноотклоняется и принимается гипотеза Н1 — о различиях.