по написанию и оформлению курсовой и выпускной квалификационной работы по психологии 4 глава

Для применения t - критерия Стьюдента необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отно­шений.

2. Сравниваемые выборки должны быть распределены по нор­мальному закону.

 

8.5.2. F — критерий Фишера

Критерий Фишера позволяет сравнивать величины выбороч­ных дисперсий двух рядов наблюдений. Для вычисления F_эмпнуж­но найти отношение дисперсий двух выборок, причем так, что­бы большая по величине дисперсия находилась бы в числителе, а меньшая знаменателе. Формула вычисления по критерию Фи­шера F такова: F_эмп

Где

и

Поскольку, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значе­ние F_эмп всегда будет больше или равно единице, т.е. F_эмп 1. Чис­ло степеней свободы определяется также просто: df₂ = n2 -1 для первой (т.е. для той выборки, величина дисперсии которой боль­ше) и df₂ = n2 - 1 для второй выборки. В таблице 18 Приложе­ния 6 критические значения критерия Фишера находятся по величинам df₁(верхняя строчка таблицы) и df₂(левый столбец таблицы).

Пример: Вдвух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос - есть ли различия в степени однородности показателей умственного развития между классами.

Для критерия Фишера необходимо сравнить дис­персии тестовых оценок в обоих классах. Резуль­таты тестирования представлены в табл. 11.

Таблица 10

№ учащихся	Первый класс X	Второй класс Y
Суммы
Среднее	60,6	63,6

 

Как видно из табл. 11, величины средних в обеих группах практически совпадают между собой 60,6 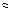63, 6 и величина t – критерия Стьюдента оказалась равной 0, 347 и незначимой.

Рассчитав дисперсии для переменных X и Y, получаем

Тогда, по формуле для расчета по F - критерию Фишера находим:

F_эмп

По табл. 18 приложения 6 для F – критерия при степенях свободы в обоих случаях равных df = 10 – 1 = 9 находим :

3,18 для P 0,05

5,35 для P 0,01

Строим «ось значимости»:

Таким образом, полученная величина F попала в зону неопределенности. В терминах статистических гипотез можно утверждать, что Н_о (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н₁. Психолог может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.

Для применения критерия F Фишера необходимо соблюдать следующие условия:

1. Измерение может быть проведено в шкале интервалов и отношений.

2. Сравниваемые выборки должны быть распределены по нормальному закону.

 

8.6. Корреляционный анализ

 

Корреляцией называют зависимость между двумя переменными величинами.

Переменная – это любая величина, которая может быть измерена и чье количественное выражение может варьировать.

При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то увеличение одного показателя сопровождается возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.

Коэффициент корреляции – это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен +1, а при полной отрицательной -1.

В случаи, если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной.

Можно выделить несколько видов корреляционного анализа: линейный, ранговый, парный и множественный. Мы рассмотрим два вида корреляционного анализа – линейный и ранговый.

 

8.6.1. Коэффициент корреляции Пирсона

 

Линейный корреляционный анализ позволяет установить прямые связи между переменными величинами по их абсолютным значениям. Формула расчета коэффициента корреля­ции построена таким образом, что если связь между признаками имеет линейный характер, коэффициент Пирсона точно устанавливает тесноту этой связи. Поэтому он называется также коэффициентом линейной корреля­ции Пирсона.

В общем виде формула для подсчета коэффициента корреля­ции такова:

где - значения, принимаемые переменной X,

- значения, принимаемые переменой Y,

- средняя по X,

- средняя по Y.

Расчет коэффициента корреляции Пирсона предполагает, что переменные X и Y распределены нормально.

Даная формула предполагает, что из каждого значения переменной X, должно вычитаться ее среднее значение . Это не удобно, поэтому для расчета коэффициента корреляции используют не данную формулу, а ее аналог, получаемый с помощью преобразований:

Используя данную формулу, решим следующую задачу:

Пример: 20 школьникам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Психолога интересует вопрос: существует ли вза­имосвязь между временем решения этих задач? Переменная X - обозначает среднее время реше­ния наглядно-образных, а переменная Y - сред­нее время решения вербальных заданий тестов.

Для решения данной задачи представим исходные данные в виде табл. 12, в которой введены дополнительные столбцы, необходимые для расчета по формуле

В табл. 12 даны индивидуальные значения переменных X и Y, построчные произведения переменных X и Y, квадраты переменных всех индивидуальных значений переменных X и Y, а также суммы всех вышеперечисленных величин.

Таблица 11

№ испытуемых	X	Y	X Y	X X	Y Y
Среднее время решения наглядно-образных заданий	Среднее время решения вербальных заданий
Сумма

 

Рассчитываем эмпирическую величину коэффициента корреляции по формуле:

Определяем критические значения для полученного коэффициента корреляции по табл. 19 приложения 6.

Отметим, что в табл. 19 приложения 6 величины критических значений коэффициентов линейной корреляции Пирсона даны по абсолютной величине. Следовательно, при получении как положительного, так и отрицательного коэффициента корреляции по формуле оценка уровня значимости этого коэффициента проводится по той же таблице приложения без учета знака, а знак добавляется для дальнейшей интерпретации характера связи между переменными X и Y.

При нахождении критических значений для вычисленного коэффициента корреляции Пирсона число степеней свободы рассчитывается как k = n – 2. В нашем случае k = 20, поэтому n – 2 = 20 – 2 = 18. В первом столбце табл. 19 приложения 6 в строке, обозначенной числом 18, находим r :

0,44 для P 0,05

0,56 для P 0,01

Строим соответствующую «ось значимости»:

 

Ввиду того, что величина расчетного коэффициента корреляции попала в зону значимости - Н_о отвергается и принимается гипотеза Н_1. Иными словами, связь между временем решения наглядно-образных и вербальных задач статистически значима на 1% уровне и положительна. Полученная прямо про­порциональная зависимость говорит о том, что чем выше сред­нее время решения наглядно-образных задач, тем выше среднее время решения вербальных и наоборот.

Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть получены в интер­вальной шкале или шкале отношений.

2. Распределения переменных X и Y должны быть близки к нор­мальному.

3. Число варьирующих признаков в сравниваемых переменных Xи Y должно быть одинаковым.

4. Таблицы уровней значимости для коэффициента корреляции Пирсона (таблица 19 приложения 6) рассчитаны от n= 5 до n= 1000. Оценка уровня значимости по таблицам осуществ­ляется при числе степеней свободы k = n - 2.

8.6.2. Коэффициент корреляции рангов Спирмена

Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи меж­ду переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о ха­рактере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядко­вых признаков, которые в этом случае представляют собой ран­ги сравниваемых величин.

Величина коэффициента корреляции Спирмена также лежит в интервале +1 и -1. Он, как и коэффициент Пир­сона, может быть положительным и отрицательным, характери­зуя направленность связи между двумя признаками, измеренны­ми в ранговой шкале.

В принципе число ранжируемых признаков (качеств, черт и т.п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков — затруднителен. Возможно, что именно поэтому таблица критических значений рангового коэф­фициента корреляции рассчитана лишь для сорока ранжируемых признаков (n <40, табл. 20 приложения 6).

Ранговый коэффициент корреляции Спирмена подсчитывается по формуле:

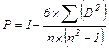
где n — количество ранжируемых признаков (показателей, ис­пытуемых);

D— разность между рангами по двум переменным для каж­дого испытуемого;

— сумма квадратов разностей рангов.

Используя ранговый коэффициент корреляции, рассмотрим следующий пример.

Пример: Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.

Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в шко­лу, и, во-вторых, итоговые показатели успевае­мости в конце года у этих же учащихся в среднем. Результаты представим в табл. 13.

Таблица 12

№ учащихся
Ранги показателей школьной готовности
Ранги среднегодовой успеваемости
		-2	-2	-2			-2		-2

 

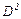
Подставляем полученные данные в формулу и производим расчет. Получаем:

Для нахождения уровня значимости обращаемся к табл. 20 приложения 6, в которой приведены критические значения для коэффициентов ранговой корреляции.

Подчеркнем, что в табл. 20 приложения 6, как и в таблице для линейной корреляции Пирсона, все величины коэффициентов корреляции даны по абсолютной величине. Поэтому, знак коэффициента корреляции учитывается только при его интерпретации.

Нахождение уровней значимости в данной таблице осуществляется по числу n, т. е. по числу испытуемых. В нашем случае n = 11. Для этого числа находим r :

0,61 для P 0,05

0,76 для P 0,01

Строим соответствующую «ось значимости»:

 

Полученный коэффициент корреляции совпал с критическим значением для уровня значимости в 1%. Следовательно, можно утверждать, что показатели школьной готовности и итоговые оценки первоклассников связаны положительной корреляционной зависимостью – иначе говоря, чем выше показатель школьной готовности, тем лучше учится первоклассник. В терминах статистических гипотез психолог должен отклонить нулевую (Н_о) гипотезу о сходстве и принять альтернативную (Н₁) о наличии различий, которая говорит о том, что связь между показателями школьной готовности и средней успеваемостью отлична от нуля.

Случай одинаковых (равных) рангов

При наличии одинаковых рангов формула расчета коэффи­циента линейной корреляции Спирмена будет несколько иной. В этом случае в формулу вычисления коэффициентов корреляции добавляются два новых члена, учитывающие одинаковые ранги. Они называются поправками на одинаковые ранги и добавляют­ся в числитель расчетной формулы.

где n - число одинаковых рангов в первом столбце,

k - число одинаковых рангов во втором столбце.

Если имеется две группы одинаковых рангов, в каком-либо столбце то формула поправки несколько усложняется:

где n - число одинаковых рангов в первой группе ранжируемого столбца,

k - число одинаковых рангов в второй группе ранжируемого столбца. Модификация формулы в общем случае такова:

 

Пример: Психолог, используя тест умственного развития (ШТУР) проводит исследование интеллекта у 12 учащихся 9 класса. Одновременно с этим, но просит учителей литературы и математики провести ранжирование этих же учащихся по показателям умственного развития. Задача заключается в том, чтобы определить, как связаны между собой объективные показатели умственного развития (данные ШТУРа) и экспертные оценки учителей.

Экспериментальные данные этой задачи и дополнительные столбцы, необходимые для расчета коэффициента корреляции Спирмена, представим в виде табл. 14.

Таблица 13

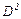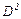№ учащихся	Ранги тестирования с помощью ШТУРа	Экспертные оценки учителей по математики	Экспертные оценки учителей по литературе	D (второго и третьего столбцов)	D (второго и четвертого столбцов)	(второго и третьего столбцов)	(второго и четвертого столбцов)
				-3	-1
				-4	-3
					-6
	2,5			0,5	-8,5	0,25	77,25
	2,5			-0,5	-8,5	0,25	77,25
				-3
				-1
					-8
Суммы						66,5	471,5

 

Поскольку при ранжировании использовались одинаковые ранги, то необходимо проверить правильность ранжирования во втором, третьем и четвертом столбцах таблицы. Суммирование в каждом из этих столбцов дает одинаковую сумму – 78.

Проверяем по расчетной формуле. Проверка дает:

В пятом и шестом столбцах таблицы приведены величины разности рангов между экспертными оценками психолога по тесту ШТУР для каждого ученика и величинами экспертных оценок учителей, соответственно по математике и литературе. Сумма величин разностей рангов должна быть равна нулю. Суммирование величин D в пятом и шестом столбцах дало искомый результат. Следовательно, вычитание рангов проведено правильно. Подобную проверку необходимо делать каждый раз при проведении сложных видов ранжирования.

Прежде, чем начать расчет по формуле необходимо рассчитать поправки на одинаковые ранги для второго, третьего и четвертого столбцов таблицы.

В нашем случае во втором столбце таблицы два одинаковых ранга, следовательно, по формуле величина поправки D1 будет:

В третьем столбце три одинаковых ранга, следовательно, по формуле величина поправки D2 будет:

В четвертом столбце таблицы две группы по три одинаковых ранга, следовательно, по формуле величина поправки D3 будет:

Прежде, чем преступить к решению задачи, напомним, что психолог выясняет два вопроса – как связаны величины рангов по тесту ШТУР с экспертными оценками по математике и литературе. Именно поэтому расчет проводится дважды.

Считаем первый ранговый коэффициент 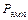с учетом добавок по формуле. Получаем:

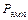
Подсчитаем без учета добавки:

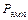
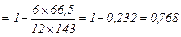
Как видим, разница в величинах коэффициентов корреляции оказалась очень незначительной.

Считаем второй ранговый коэффициент 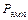с учетом добавок по формуле. Получаем:

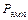
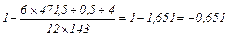
Подсчитаем без учета добавки:

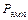
И опять, различия оказались очень незначительны. Поскольку число учащихся в обоих случаях одинаково, по табл. 20 приложения 6 находим критические значения при n = 12 сразу для обоих коэффициентов корреляции.

0,58 для P 0,05

0,73 для P 0,01

Откладываем первое значение 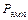на «оси значимости»:

 

 

В первом случае полученный коэффициент ранговой корреляции находится в зоне значимости. Поэтому психолог должен отклонить нулевую Н_о гипотезу о сходстве коэффициента корреляции с нулем и принять альтернативную Н₁ о значимом отличии коэффициента корреляции от нуля. Иными словами, полученный результат говорит о том, что чем выше экспертные оценки учащихся по тесту ШТУР, тем выше их экспертные оценки по математике.

Откладываем второе значение 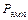на «оси значимости»:

 

Во втором случае коэффициент ранговой корреляции находится в зоне неопределенности. Поэтому психолог может принять нулевую Н_о гипотезу о сходстве коэффициента корреляции с нулем и отклонить альтернативную Н₁ о значимом отличии коэффициента корреляции от нуля. В этом случае полученный результат говорит о том, что экспертные оценки учащихся по тесту ШТУР не связаны с экспертными оценками по литературе.

Для применения коэффициента корреляции Спирмена, необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и отношений.

2. Характер распределения коррелируемых величин не имеет значения.

3. Число варьирующих признаков в сравниваемых переменных Xи Y должно быть одинаковым.

Таблицы для определения критических значений коэффициента корреляции Спирмена (табл. 20 приложение 6) рассчитаны от числа признаков равных n = 5 до n = 40 и при большем числе сравниваемых переменных следует использовать таблицу для пирсоновского коэффициента корреляции (табл. 19 приложение 6). Нахождение критических значений осуществляется при k = n.

 

Содержание

 

Введение……………………………………………………………………………………………………..4

 

1. Этапы и сроки выполнения работы………………………………………………………………… …5

2. Требования к объему и структуре работы………………………………………………………………5

3. Выбор темы курсовой и выпускной квалификационной работе……………………………………..5

4. Содержание курсовой и выпускной квалификационной работ……………………………………….5

4.1 Ведение…………………………………………………………………………………………...7

4.2 Теоретическая часть работы…………………………………………………………………….8

4.3 Практическая часть работы……………………………………………………………………...8

4.4. Заключение………………………………………………………………………………………9

4.5. Выводы…………………………………………………………………………………………..9

4.6. Библиографический список…………………………………………………………………….9

4.7. Приложения……………………………………………………………………………………...9

5. Общие требования к оформлению курсовой и выпускной квалификационной работы…………...10

6. Требования к языку и стилю работы……………………………………………………………………10

6.1. Оформление титульного листа………………………………………………………………..10

6.2. Оформление содержания………………………………………………………………………10

6.3. Оформление заголовков……………………………………………………………………….10

6.4. Оформление таблиц……………………………………………………………………………11

6.5. Оформление иллюстраций………………………………………………………………….....11

6.6. Оформление библиографического списка……………………………………………………13

6.7. Оформление библиографических ссылок…………………………………………………….14

6.8. Оформление приложений……………………………………………………………………...14

7. Типичные недостатки оформления курсовой и выпускной квалификационной работы…………...15

8. Статистическая обработка результатов исследования………………………………………………...15