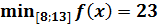Практическая работа
Тема: «Исследование функции. Вычисление производных, нахождение дифференциалов»
Цели: научиться проводить исследование функции с помощью производной и строить графики функций; закрепить основные признаки возрастания (убывания) функции, условия существования точек экстремума; проводить исследование функции по графику производной.
Краткая теоретическая справка
1. Находим область определения D(f) функции y = f(x).
2. Проверяем функцию на четность.
Если f(-x) = f(x), то функция четная, график функции симметричен относительно оси OY.
Если f(-x) = - f(x), то функция нечетная, график нечетной функции симметричен относительно начала координат.
В противном случае функция является ни четной, ни нечетной.
3. Если функция периодическая, то находим период функции.
4. Находим точки пересечения графика с осями координат.
Находим нули функции - это точки пересечения графика функции с осью абсцисс (Ox).
Для этого мы решаем уравнение f(x) = 0.
Находим точку пересечения графика функции с осью ординат (Oy). Для этого ищем значение функции при x=0.
5. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции, нам нужно решить неравенства 
f(x) >0 и f(x) <0 .
6. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную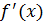 
б) Приравниваем производную к нулю и находим корни уравнения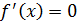 
- это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
7. Найти значения функции в точках экстремума.
8. По данным исследования построить график функции.
Пример 1. Исследовать функцию и по результатам исследования построить график.
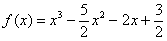
Решение.
1) D(f): R
2) Проверим функцию на чётность/нечётность:
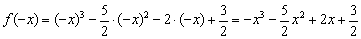
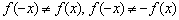, значит, данная функция не является чётной или нечётной.
3) Функция непериодическая.
4) Нули функции.
С осью Оy:
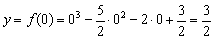
Чтобы найти точки пересечения с осью Ox (нули функции) требуется решить уравнение f(x) = 0:
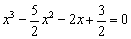
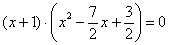
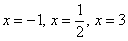
5) Таким образом, на интервалах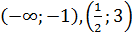 
график расположен ниже оси абсцисс f(x)<0, а на интервалах 
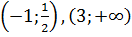– выше данной оси f(x) >0.
6) Возрастание, убывание.
Найдём критические точки:
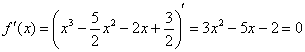
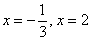
Отложим их на числовой прямой и определим знаки производной:
1 
Следовательно, функция возрастает на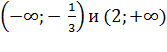 
и убывает на 
.
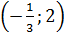7). Экстремумы функции
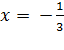точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»
. 
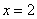точка минимума, так как при переходе через нее производная меняет знак с «-» на «+».
8). 
: 
.
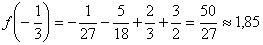
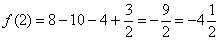9) Строим график функции.
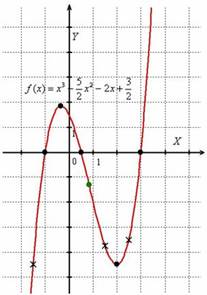
Пример 2. На рисунке изображен график производной функции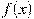 
, определенной на интервале 
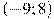. В какой точке отрезка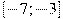 
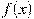принимает наибольшее значение.
Решение. На отрезке [-7;-3] график производной расположен ниже оси Ох, это означает, что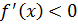 
, то есть сама функция на данном отрезке монотонно убывает. Таким образом, убывающая функция принимает наибольшего значения на левом конце промежутка, то есть в точке x=-7.
Ответ. -7.
Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти производную функции.
- Определить критические точки (те точки, в которых производная функции обращается в ноль или не существует).
- Выбрать из найденных точек те, которые принадлежат данному отрезку.
- Вычислить значения функции (не производной!) в этих точках и на концах отрезка.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 3. Найдите наименьшее значение функции y = x 3 – 18 x 2 + 81 x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
1) y’ = 3 x 2 – 36 x + 81.
2) y’ = 3 x 2 – 36 x + 81 = 0
x 2 – 12 x + 27 = 0,
x = 3 и x = 9
3) x = 9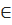 
[8; 13].
4) y = x 3 – 18 x 2 + 81 x + 23 = x (x -9)2+23:
o y (8) = 8 · (8-9)2+23 = 31;
o y (9) = 9 · (9-9)2+23 = 23;
o y (13) = 13 · (13-9)2+23 = 231.
Ответ.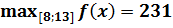 
; 