МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ№ 1
Указания к решению задачи 1
Решение задачи 1 требует знания основных законов постоянного тока, производных формул этих законов и умения их применять для расчета электрических цепей со смешанным соединением резисторов.
Методику и последовательность действий при решении задач со смешанным соединением резисторов рассмотрим в общем виде на конкретных примерах.
Пример1 На рисунке 2 изображена электрическая цепь со смешанным соединением резисторов. Известны значения сопротивлений резисторов R1 = 3 Ом, R2 = 10 Ом, R3 = 15 Ом, R4 = 1 Ом, напряжение U= 110 B и время работы цепи t = 10 ч. Определить токи, проходящие через каждый резистор, I1, I2, I3, I4, общую мощность цепи Р и расход энергии W.
Дано: R1 = 3 Ом, R2 = 10 Ом, R3 = 15 Ом, R4 = 1 Ом, U= 110 B, t = 10 ч. Определить: I1, I2, I3, I4
Решение
1 Обозначим стрелками токи, проходящие через каждый резистор, с учетом их направления. (рисунок 2).
2 Определим общее эквивалентное сопротивление цепи, метод подсчета которого для цепи со смешанным соединением резисторов сводится к последовательному упрощению схемы.
Сопротивления R2 и R3 соединены параллельно. Найдем общее сопротивление при таком соединении:
1/R23 =1/R2+1/R3,
приводя к общему знаменателю, получим
R23 = R2R3/(R2+R3) = 10 ∙15/(10+15) = 150/25 = 6 Ом.
Схема примет вид рисунок 3.
Теперь резисторы R23, R1, R4 соединены последовательно, их общее сопротивление
Rэк = R1+R23+R4=3+6+1=10 Ом.
Это общее сопротивление, включенное в цепь вместо четырех сопротивлений схемы (рисунок 2), при таком значении напряжения не изменит тока в цепи. Поэтому это сопротивление чаще называется общим эквивалентным сопротивлением цепи или просто эквивалентным (рисунок 4).
|
|
Рисунок 2 Рисунок 3 Рисунок 4
3 По закону Ома для внешнего участка цепи определим ток I=U/Rэк=110/10 =11А.
4 Найдем токи, проходящие через все резисторы. Через резистор R1 проходит ток I1 = I. Через резистор R4 проходит ток I4 =I.
Для определения токов, проходящих через резисторы R2 и R3, нужно найти напряжение на параллельном участке U23. Это напряжение можно определить двумя способами:
U23 = IR23 = 11 ∙ 6 = 66 В
или U23 = U-IR1-IR4 = U-I(R1+R4) = 110 - 11(3+1) = 66 В.
По закону Ома для параллельного участка цепи найдем
I2 = U23/R2 = 66/10 = 6,6 A; I3 = U23/R3 = 66/15 = 4,4 A или,
Применяя первый закон Кирхгофа, получим
I3 = I-I2 = 11 - 6,6 = 4,4 A.
5 Найдем общую мощность цепи:
I = UI = 110 ∙ 11 = 1210 Вт = 12,1 кВт
6 Определим расход энергии:
W = Rt = 1,21 ∙ 10 = 12,1 кВт ∙ ч
7 Выполним проверку решения задачи описанными ранее способами:
а) проверим баланс мощности
P = P1 +P2+ P3 + P4 = I12R1 + I22R2+I32R3+I42R4 = 112∙3 + 6,6 2 ∙ 10+ 4,42∙15 + 112 ∙ 1 = 363 + 435,6 + 290,4 + 121 = 1210 Вт; 1210 Вт = 1210 Вт;
б) для узловой точки А схемы рисунка 2 применим первый закон Кирхгофа:
I = I2 + I3 = 11 = 6,6 + 4,4 A; 11A = 11A;
в) составим уравнение по второму закону Кирхгофа, обходя контур цепи по часовой стрелке,
U = U1 + U23 + U4 = IR1 + IR23 + IR4
110 = 11 ∙ 3 + 11 ∙6 + 11 ∙ 1
110 В = 110 В
Все способы проверки подтверждают правильность решения задачи. В вашем варианте достаточно использовать только тот способ, который предусмотрен условием.
Пример2. Определить эквивалентное сопротивление цепи, силу тока в неразветвлённой части цепи (или напряжение, приложенное к цепи), а также токи и напряжение на каждом участке цепи по приведённой схеме. Индекс тока (и напряжения) должен соответствовать индексу R соответствующего резистора.
|
|
Данные своего варианта взять в таблице.
| R3 |
| R2 |
| R1 |
| № варианта | R1 (Ом) | R2 (Ом) | R3 (Ом) | R4 (Ом) | I (А) | U (В) |
| - |
| R4 |
I I4
U
Решение
1.Определим эквивалентное сопротивление цепи
а) Т.к. цепь имеет смешанное соединение решать будем используя метод упрощения цепи. Резисторы 1,2 и 3 соединены последовательно, их сопротивление
б) Упростим схему, заменив эти резисторы одним 
.
| R123 |
| R1 |
U
в) определим эквивалентное сопротивление цепи
или 
= 36Ом
2. Определим силу тока в цепи.
= 
3. Определим токи и напряжения на каждом участке цепи.
а) сначала определим токи и напряжения на упрощенной схеме, так как резисторы R123 и R4 соединены параллельно: 
; токи определим применяя закон Ома для участка цепи 
; 
.
б) определим токи и напряжения на участке который упрощали, так как резисторы соединены последовательно: 
; напряжения определим используя закон Ома для участка цепи 
Указания к решению задачи 2.
Эта задача относятся к неразветвленным и разветвленным цепям переменного тока. Перед их решением изучите материал темы 1.4 Электрические цепи переменного тока, ознакомьтесь с методикой построения векторных диаграмм, рассмотренной ниже. Разберите решение типовых примеров 3, 4.
Пример 3 Активное сопротивление катушкиRк = 6Ом, индуктивность ее L = 0,0318Гн. Последовательно с катушкой включено активное сопротивление R1 = 2Ом и конденсатор емкостью С =795мкф. К цепи приложено напряжение U = 100B (действующее значение). Определить: полное сопротивление цепи; силу тока; коэффициент мощности; угол сдвига фаз, активную, реактивную и полную мощности; напряжения на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи. Частота тока в цепи f = 50 Гц.
|
|
L
| R1 |
| Rк |
C
U
Решение
1) Индуктивное сопротивление катушки и емкостное сопротивление конденсатора не заданы, поэтомуопределяем их по формулам:
= 2 
2) Полное сопротивление цепи
, где R - активное сопротивление всей ветви. Х – реактивное сопротивление всей ветви.
R = Rк + R1 = 6 + 2 = 8 Ом.
X = XL – Xc = 10 – 4 = 6 Ом.
.
3) Сила тока в цепи
4) Коэффициент мощности
5) Угол сдвига фаз между колебаниями тока и напряжения
.
Определяя угол сдвига фаз через четную функцию косинус, мы теряем знак угла. Поэтому в тех случаях, где важен знак угла, следует пользоваться нечетными его функциями (синусом или тангенсом). В нашем примере
.
Знак плюс у угла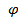 
показывает, что напряжение опережает ток.
6) Активная мощность
.
или 
7) Реактивная мощность
Или 
8) Полная мощность
Или 
.
9) Напряжения на сопротивлениях цепи:
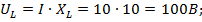
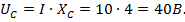
10) Для построения векторной диаграммы выберем масштаб по току и по напряжению: по току 
по напряжению - 
. И определим линейные размеры строящихся векторов.
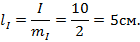
Построение начинаем с вектора силы тока (т.к. он одинаков на всех участках цепи),который откладываем по горизонтали определенной длины-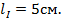 
Из начала вектора силы тока строим вектор 
,длиной 
откладывая его вдоль вектора тока 
. Из конца вектора строим вектор напряжения 
, длиной 
, откладывая его в сторону опережения вектора тока на 
. Из конца вектора строим вектор напряжения 
, длиной 
откладывая его вдоль вектора силы тока. Из конца вектора напряжения
строим вектор напряжения 
, длиной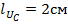 
, откладывая его в сторону отставания от вектора тока на . Геометрическая сумма векторов , , 
и представляет вектор полного напряжения 
, приложенного к цепи.
Пример 4 Катушка с активным сопротивлением R=20 Ом и индуктивным 
соединена параллельно с конденсатором, емкостное сопротивление которого 
. Определить: токи в ветвях и в неразветвленной части цепи; активные и реактивные мощности ветвей и всей цепи; полную мощность цепи; углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму. К цепи приложено напряжение U=100B.
I
| R |
I1
U 
Решение. 1)Полное сопротивление первой ветви
; 
; 
.
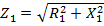2) Полное сопротивление второй ветви
; 
; 
; 
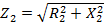= 50 Ом.
3) Сила тока в первой ветви
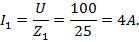
4) Сила тока во второй ветви
5) Углы сдвига фаз в ветвях будем находить по синусам во избежание потери знаков углов:
.
. Знак – означает, что во второй ветви напряжение отстает от тока.
6) Активные мощности ветвей и всей цепи
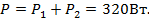
7) Реактивные мощности ветвей и всей цепи
Обращаем ваше внимание на то, что реактивная мощность конденсатора имеет обратный знак по сравнению с реактивной мощностью катушки.
8) Полная мощность цепи
9) Сила тока в неразветвленной части цепи
10) Угол сдвига фаз в неразветвленной части цепи
11) Перед построением векторной диаграммы определим активные и реактивные составляющие токов ветвей.
знак - означает, что напряжение отстает от тока.
12) Для построения векторной диаграммы зададимся масштабом по току и напряжению: по току - 
по напряжению - 
. И определим линейные размеры строящихся векторов.
Построение начинаем с вектора напряжения, который откладываем по горизонтали, длиной 
Из начала вектора напряжения стоим вектора токов ветвей. Вектор силы тока первой ветви строим как геометрическую сумму его активной и реактивной составляющих - 
. Вектор 
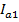, длиной 6,4см строим вдоль вектора напряжения, из его конца строим вектор 
, длиной 4,8см под углом к вектору напряжения в сторону отставания. Вектор силы тока второй ветви строим также как геометрическую сумму его активной и реактивной составляющих - 
. Т.к. 
, данный вектор, длиной 4,0см, строим под углом к вектору напряжения в сторону опережения. Вектор тока в неразветвленной части цепи строим как геометрическую сумму векторов токов в ветвях цепи - 
.
.
