Указания к решению задачи 3

Для решения задачи 3 нужно знать программный материал темы "трехфазные цепи", отчетливо представлять соотношения между фазными и линейными значениями токов и напряжений при соединении потребителей электрической энергии звездой и треугольником. При затруднениях в применении формул и понимании физических процессов в трехфазных цепях рекомендуется использовать учебный материал.

Для ознакомления с общей методикой решения задач данной темы приведены формулы, показано их практическое применение.

Соединение потребителей звездой. На рисунке 12 а - в показано разное выполнение схем такого соединения с нейтральным проводом и без него. Принятые обозначения на схемах: линейное напряжение

U_л = U_AB = U_BC = U_CA;

фазные напряжения U_ф, U_A, U_В, U_С, линейные токи (они же фазные токи) I_л, I_ф, I_A, I_B, I_C, ток в нейтральном проводе, равный геометрической сумме фазных токов

.

При одинаковой нагрузке фаз ток I₀ = 0 и надобность в нем отпадает (рисунок 12).

 

Соединение потребителей треугольником На рисунке 13 а,б показано разное выполнение схем такого соединения. Принятые обозначения на схемах: линейные (они же фазные) напряжения

U_л = U_ф = U_AB= U_BC = U_CA,

фазные токи I_ф, I_AB, I_BC, I_CA, линейные токи I_л; I_A; I_B; I_C.

Подсчет активной мощности для любого соединения в трехфазных цепях выполняется по формулам: фазные мощности

Р_ф1 = U_ф1I_ф1 cos φ_ф1

; Р_ф2 = U_ф2I_ф2 cos φ_ф2;

Р_ф3 = U_ф3Iф₃ cos_ф3,

а общая мощность

Р = Р_ф1+ Р_ф2 + Р_ф3.

 

 

 

 

Рисунок 12

 

 

Рисунок 13

 

Рисунок 14

 

 

При одинаковой нагрузке фаз

Р = U_лI_л cos φ_ф.

Для подсчета параметров ламп накаливания и электронагревательных элементов ТЭН нужно применять формулы

P_нагр = U_нагр I_нагр ∙ cos φ_нагр;

Р_ламп = U_лампI_ламп cos φ_ламп,

учитывая, что cos φ_ламп= cos φ_нагр = 1, так как эта нагрузка активная. Применение формул рассмотрим в решенных примерах.

Пример 5. Три одинаковых потребителя, имеющих активные сопротивления R_ф1 = R_ф2 = R_ф3 = 10 Ом, соединены треугольником (рисунок 14) и подключены к трехфазной электрической цепи с линейным напряжением U_л = 220 В. Определить: фазные I_AB, I_BC, I_CA и линейные I_A,I_B,I_C токи, фазные мощности Р_АВ, Р_ВС, Р_СА и общую активную мощность трехфазной цепи Р.

Дано: R_ф1 = R_ф2 = R_ф3 = 10 Ом, U_л = 220 В.

Определить: I_AB, I_BC, I_CA, I_A,I_B,I_C, Р_АВ, Р_ВС, Р_СА

Решение

1. Фазные точки I_AB, I_BC, I_CA определим по закону Ома для фазы

I_ф = U_ф/Z_ф.

По условию задачи все фазы нагружены одинаково сопротивлениями R = 10 Ом. При соединении треугольником линейные напряжения равны фазным, значит, в данном случае U_ф = 220 В. Тогда

I_ф = I_AB = I_BC = I_CA = U_ф/R = 220/10 = 22 A

 

2. Линейные токи найдены по формуле, определяющей соотношение между линейными и фазными токами при одинаковой нагрузке фаз, что соответствует условиям задачи:

I_A = I_B = I_C= I_ф = 1,73 · 22 = 38 А.

3. Фазные мощности определим по формуле

Р_ф = Р_АВ = Р_ВС = Р_СА = I²R_ф = 222 · 10 = 4840 Вт.

Тогда мощность цепи

Р = 3Р_ф= 3 · 4840 = 14520 Вт = 14,5 кВт.

Так как нагрузка фаз одинаковая, мощность цепи также можно найти по формуле

Р = U_лI_лcosφ_ф = 1,73 · 220 · 38 · 1 = 14480 Вт = 14,5 кВт.

Пример 6. Три активных сопротивления R_ф1 = 10 Ом, R_ф2 = 20 Ом, R_ф3 = 5 Ом соединены звездой с нейтральным проводом и присоединены четырехпроводной трехфазной линии с линейным напряжением

U_л = 220В (рисунок 17). Определить: 1) фазные токи I_ф1, I_ф2, I_ф3; 2) ток в нулевом (нейтральном проводе I₀; 3) фазные мощности Р_ф1, Р_ф2, Р_ф3; 4) общую активную мощность трехфазного потребителя энергии Р.

 

Дано: U_л = 220 В, R_ф1 = 10 Ом, R_ф2 = 20 Ом, R_ф3 = 5 Ом.

Определить: I_ф1, I_ф2, I_ф3, Р_ф1, Р_ф2, Р_ф3, Р.

Рисунок 17

Решение

При наличии нейтрального провода при любой нагрузке (равномерной или неравномерной) справедливо соотношение между фазным U_ф и линейным U_л напряжением

U_ф = U_л/ ,

U_ф = 220/ 1,73 = 127 В.

Помня, что нейтральный провод при любых нагрузках обеспечивает равенство фазных напряжений приемников энергии, получим

U_ф = U_A=U_B=U_C=127 B.

1. Определяем значение фазных (они же линейные) токов по закону Ома:

I_ф1 = I_A = U_ф/R_ф1 = 127/10 = 12,7 А;

I_ф2 = I_B = U_ф/R_ф2 = 127/20 = 6,35 А;

I_ф3 = I_C =U_ф/R_ф3 = 127/5 = 25,4 А.

2. Нагрузка чисто активная, поэтому мощности фаз определяем по тем же формулам, которые применялись в примере 5.

Р_ф1 = Р_А = I²_ф1R_ф1 = 12,7² · 10 = 161,29 · 10 = 1612,9 Вт = 1,613 кВт;

Р_ф2 = Р_В = I²_ф2R_ф2 = 6,35² · 20 = 806,45 Вт = 0,806 кВт;

Р_ф3 = Р_С = I²_ф3R_ф3 = 25,4² · 5 = 645,16 · 5 = 322,8 Вт = 3,228 кВт.

3. Активную мощность трехфазного потребителя энергии Р определим как сумму мощностей трех фаз:

Р = Р_А+Р_В+Р_С = 1,613 + 0,806+3,226=5,645 кВт.

4. Для определения тока в нейтральном проводе при соединении приемников энергии звездой нужно построить векторную диаграмму, придерживаясь такой последовательности:

 

4.1. Выписываем значения вычислительных напряжений и токов: фазные напряжения U_ф = U_A = U_B = U_C = 127 B, фазные (линейные) токи I_A = 12,7 A; I_B = 6,35 A; I_C = 25,4 A.

 

 

4.2. Задаемся масштабом: по напряжению m_U = 30 B/см, по току m₁ = 7 А/см.

4.3. Определяем длину векторов напряжения и токов:

 

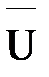L _A=L _B=L 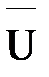_C=U_ф/m_U = 127 B/30 B/см = 4,23 см;

L_IA = I_A/m₁ = 12,7 А/7 А/см = 1,81 см;

L_IB = I_B/m₁= 6,35 A/7 A/см = 0,9 см;

L_IC = I_C/m₁ = 25,4 А/7 А/см = 3,62 см.

 

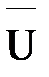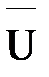4.4. Откладываем векторы фазных напряжений _А, _В, 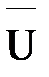_С найденной длины под углом 120 ° относительно друг друга.

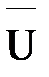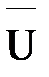4.5. В фазе с векторами фазных напряжений _А, _В, 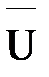_С откладываем векторы фазных токов _{А, В}, _С, так как нагрузка всех фаз активная

(φ = φ_А = φ_В = φ_С = 0).

 

Рисунок 18

 

 

4.6. Геометрическое сложение фазных токов _{А, В}, _С производим используя формулу: ₀ = _А + _В+ _с по правилу многоугольника, которое рассмотрено выше, и получим вектор тока в нейтральном проводе (рисунок 18, а). На построенной в масштабе векторной диаграмме линейкой измеряем длину вектора тока в нейтральном проводе L ₀ и, зная масштаб по току m₁, определяем числовое значение I₀: L ₀ = 2,3 см; I₀ = L ₀ m₁ = 2,3 см · 7 А/см = 16,1 А.

 

Пример 7. Осветительные лампы трех этажей ткацкой фабрики соединены звездой и присоединены к трехфазной четырехпроводной линии с линейным напряжением U_л = 380 В (рисунок 19).

Число ламп на каждом этаже одинаковое n₁ = n₂ = n₃ =50. Мощность каждой лампы Р_ламп = 100 Вт. Определить: 1) фазные токи I_A, I_B, I_C при одновременном включении всех ламп на каждом этаже; 2) фазные активные мощности Р_А, Р_В, Р_С и мощность Р всей трехфазной цепи; 3) ответить на вопрос чему будет равен ток в нейтральном проводе?

Дано: U_л = 380 В, n₁ = n₂ = n₃ =50 ламп, Р_ламп = 100 Вт.

Определить: I_A, I_B, I_C, I₀, Р_А, Р_В, Р_с, Р.

 

Решение

1. Определяем фазные мощности, исходя из того, что в каждой фазе включено по 50 ламп, Р_ламп = 100 Вт каждая:

Р_А = Р_В = Р_С = n₁P_ламп = 50 · 100 = 5000 Вт = 5 кВт.

2. Тогда мощность всей трехфазной цепи

Р = Р_А + Р_В + Р_С = 3 · 5 = 15 кВТ.

 

3. Фазные (они же линейные) токи найдем из формулы фазной мощности

Р_А = U_фI_Аcosφ_A,

предварительно определив

U_ф = U_л/ = 380/1,73 = 220 В,

cosφ_A = cosφ_B = cosφ_C = 1-(нагрузка октивная).

Тогда I_ф = I_A = I_B = I_C = Р_ф/(U_ф cosφ_ф) = 5000/(220 · 1) = 22,7 А.

4. Для подсчета тока в нулевом проводе построим без масштаба векторную диаграмму (рисунок 18, б). Векторы фазных токов будут иметь одинаковую длину, так как значения токов одинаковые. Направление их векторов вдоль соответствующих векторов фазных напряжений. Из диаграммы видно, что ток в нейтральном проводе I₀ равен нулю.