Знакоположительные ряды
(продолжение)
Интегральный признак Коши.
Теорема (интегральный признак Коши).
Пусть функция y = f (x) удовлетворяет следующим условиям:
1) принимает положительные значения на промежутке 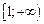 ;
;
2) является монотонно убывающей (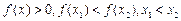 );
);
3) 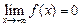 ;
;
4) 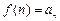 .
.
Тогда ряд 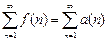 и несобственный интеграл
и несобственный интеграл 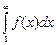 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство:
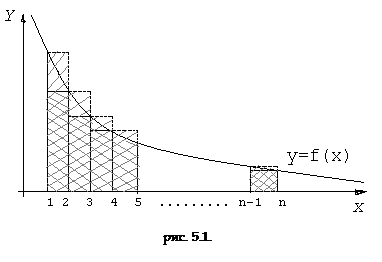 Найдем
Найдем 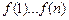 и построим ступенчатые фигуры (см. рис. 5.1):
и построим ступенчатые фигуры (см. рис. 5.1):
 -
- 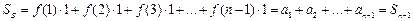 - площадь большей ступенчатой фигуры.
- площадь большей ступенчатой фигуры.
 -
- 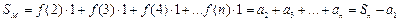 - площадь меньшей ступенчатой фигуры.
- площадь меньшей ступенчатой фигуры.
Площадь криволинейной трапеции вычисляется по формуле: 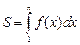 .
.
Очевидно, что:
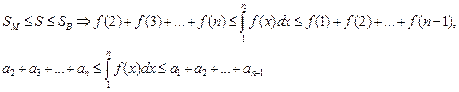 .
.
Следовательно,
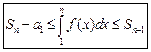 ,
,
где 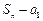 - n -ая частичная сумма без первого слагаемого,
- n -ая частичная сумма без первого слагаемого, 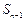 - n-1 -ая частичная сумма без первого слагаемого.
- n-1 -ая частичная сумма без первого слагаемого.
Напомним определение расходящегося интеграла:
Интеграл 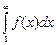 называется сходящимся, если выполняется следующее условие:
называется сходящимся, если выполняется следующее условие:
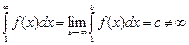 .
.
Рассмотрим 4 случая:
1) если ряд сходится, то 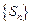 - ограниченна, следовательно,
- ограниченна, следовательно,
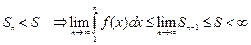 и интеграл сходится.
и интеграл сходится.
2) если ряд расходится, то 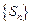 - неограниченна, следовательно,
- неограниченна, следовательно, 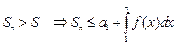 и интеграл расходится.
и интеграл расходится.
3) если интеграл сходится, то 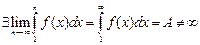 . Следовательно,
. Следовательно,
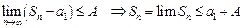 , т.е.
, т.е. 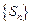 ограниченна и ряд
ограниченна и ряд 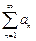 сходится (по критерию сходимости знакоположительных рядов).
сходится (по критерию сходимости знакоположительных рядов).
4) если интеграл расходится, то 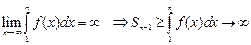 , т.е.
, т.е. 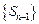 -
-
неограниченна и ряд расходится.
Ч.т.д.
Исследование поведения обобщенного гармонического ряда с помощью интегрального признака.
Мы уже отмечали, что 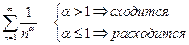 . Теперь мы это докажем.
. Теперь мы это докажем.
Пусть 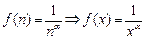 и пусть
и пусть 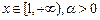 . Тогда функция y = f (x) удовлетворяет условию теоремы (см. п. 5.1).
. Тогда функция y = f (x) удовлетворяет условию теоремы (см. п. 5.1).
Рассмотрим 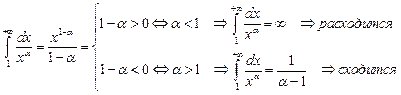 .
.
Отдельно рассмотрим случай, когда 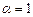 :
: 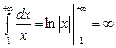 - следовательно, интеграл расходится.
- следовательно, интеграл расходится.
Замечание.
Интегральный признак удобно применять также для рядов вида
 . Действительно,
. Действительно,
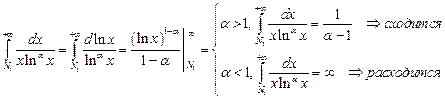 .
.
При 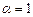 :
: 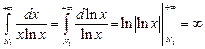 - следовательно, интеграл расходится.
- следовательно, интеграл расходится.
Оценка остатка знакоположительного ряда с помощью интегрального признака.
Из доказательства теоремы п. 5.1 следует, что
1) Оценка суммы ряда:
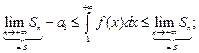
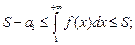
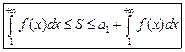
2) Оценка остатка ряда:
Напомним, что остаток rn – это ряд с первым членом an+1.
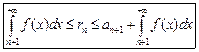
Примеры применения оценок:
1) показать справедливость неравенства 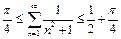 .
.
Ряд 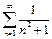 сравним с интегралом
сравним с интегралом 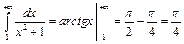 .
. 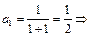 по оценке суммы
по оценке суммы 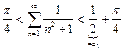 .
.
2) какую погрешность допустим, если заменим сумму ряда 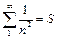 на S5?
на S5?
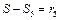 ,
, 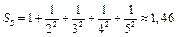 ,
, 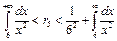 ,
,
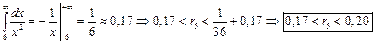 ,
, 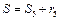 ,
, 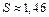 ,
, 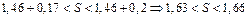 . Позже мы покажем, что
. Позже мы покажем, что 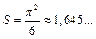 .
.
Признаки Раабе и Гаусса (необязательно).
Теорема 1 (признак Раабе).
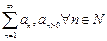 и
и 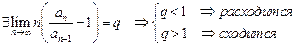
Теорема 2 (признак Гаусса).
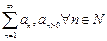 и
и 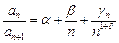 , где
, где 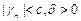 , то
, то
1) 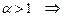 сходится;
сходится; 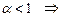 расходится.
расходится.
2) 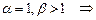 сходится;
сходится; 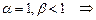 расходится.
расходится.
Обзор экзаменационных задач на исследование знакоположительных рядов.
1. Задачи на сравнение an c 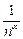 ( гармоническими рядами).
( гармоническими рядами).
Пример:
Исследовать на сходимость ряд 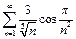 .
.
Т.к. 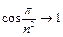 при
при  , то
, то 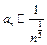 .
. 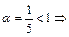 ряд расходится по сравнению с обобщенным гармоническим рядом.
ряд расходится по сравнению с обобщенным гармоническим рядом.
2. Задачи на сравнение an с геометрическими прогрессиями.
Пример:
Исследовать на сходимость ряд 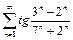 .
.
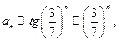 ряд
ряд 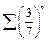 сходится, т.к. члены ряда представляют собой геометрическую прогрессию с
сходится, т.к. члены ряда представляют собой геометрическую прогрессию с 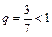 . Следовательно, исходный ряд так же сходится.
. Следовательно, исходный ряд так же сходится.
Задачи на применение необходимого признака сходимости.
Примеры:
1) Исследовать на сходимость ряд 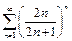 .
.
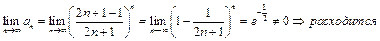
2) Исследовать на сходимость ряд 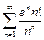 .
.
С помощью уже рассмотренной формулы Стирлинга получим: 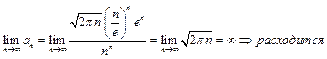 .
.
Задачи на применение признака Даламбера.
Напомним, что,
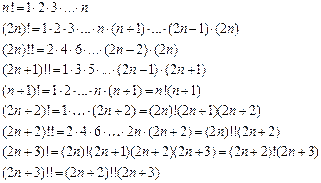
Пример:
Исследовать на сходимость ряд 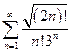 .
.
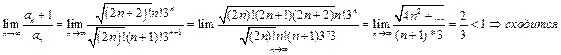 .
.
Задачи на применение радикального признака Коши.
Пример:
Исследовать на сходимость ряд 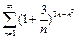 .
.
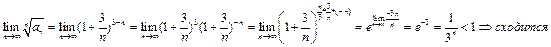 .
.