ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
СИНУСОИДАЛЬНОГО ТОКА
ОБЩИЕ СВЕДЕНИЯ
Возрастающая роль электрической энергии в развитии промышленности, транспорта и сферы услуг в конце XIX в. стимулировала теоретические и экспериментальные работы по созданию эффективных электрических устройств в технологической цепи производства, передачи и потребления электрической энергии. В настоящее время электрическая энергия для промышленных целей вырабатывается электромеханическими генераторами синусоидального тока при стандартной частоте тока 50 Гц в России и большинстве других стран (в США 60 Гц). Электромеханические генераторы с приводом от паровой турбины на тепловых и атомных электростанциях имеют мощность 100—1200 МВт. Преобразование значений параметров синусоидального тока электрогенераторов трансформаторами позволяет передавать электрическую энергию по линиям высокого напряжения (до 750 кВ) на большие расстояния (до 500 км) с минимальными потерями.
Асинхронные и синхронные двигатели синусоидального тока промышленной частоты эффективно используются для преобразования электрической энергии в различных системах электропривода подъемно-транспортных машин, станков, обрабатывающих инструментов и т. п.
Разнообразно использование синусоидального тока непромышленной частоты. В электрических печах для выплавки тугоплавких и особо чистых металлов частота синусоидального тока составляет 500 Гц÷50 кГц. В электроакустических установках частота синусоидального тока может составлять несколько герц.
Развитие радиотехники привело к созданию высокочастотных устройств (до 100 МГц): антенн, генераторов, преобразователей и т.п.
ЭЛЕМЕНТЫЭЛЕКТРИЧЕСКОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Электрическая цепь синусоидального тока содержит кроме электротехнических устройств, назначение которых совпадает с назначением функционально аналогичных устройств цепи постоянного тока (источники энергии, измерительные приборы, коммутационные аппараты и т.п.), также устройства, присущие только цепям синусоидального тока: трансформаторы, конденсаторы, катушки индуктивности и др. Совокупность электротехнических устройств в цепи синусоидального тока для наглядного и компактного отображения связей между ними представляют принципиальной схемой, аналогичной приведенной на рис. 28, где вместо батареи должен быть генератор переменного тока.
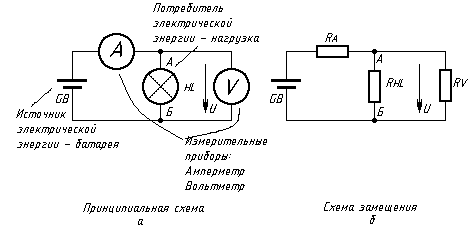
Рис. 28
Для расчета режима работы электротехнических устройств необходимо перейти от принципиальной схемы цепи к ее схеме замещения. Элементами схем замещения цепей синусоидального тока являются источники синусоидальных тока и ЭДС, резистив-ные, индуктивные и емкостные элементы.
Если параметры элементов не зависят от тока в них и приложенного к ним напряжения, то это линейные элементы. В противном случае элементы следует считать нелинейными.
ИСТОЧНИКИ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ СИНУСОИДАЛЬНОГО ТОКА
Промышленными источниками электрической энергии синусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых или гидравлических турбин преобразуется в электрическую.
Проанализируем работу такого генератора при упрощающих допущениях. Принципиальная конструкция двухполюсного электромеханического генератора изображена на рис. 29, а. Она содержит неподвижный плоский разомкнутый виток с выводами a и b и постоянный магнит, который вращается с постоянной частотой f, т. е. с постоянной угловой скоростью Ω = 2πf, рад/с, внутри витка.
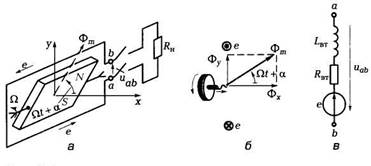
Рис. 29 Принцип получения переменного тока.
Основная единица измерения частоты f в СИ — герц (Гц): 1 Гц = 1 с-1. Величина, обратная частоте, называется периодом Т = = 1/ f, с.
Пусть магнитный поток постоянного магнита равен Фт. Из пространственного распределения магнитного потока (см. рис. 29, б) с л едует, что мгновенное значение составляющей магнитного потока, пронизывающей виток, т. е. направленной вдоль оси х, равно
Фх = Фт cos (Ω·t + α) = Фт sin (ω·t + ψФ),
где: Фт — максимальное значение (амплитуда) магнитного потока, пронизывающего виток; α — начальный (т. е. в момент t = 0, принятый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х; ω — угловая частота синусоидальной функции магнитного потока, имеющая размерность и значение, совпадающие с размерностью и значением угловой скорости Ω вращения постоянного магнита; ψФ = π/2 + α — начальная фаза магнитного потока; ω·t + ψФ — фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной функции в момент времени t = 0.
Согласно закону электромагнитной индукции, при изменении потокосцепления витка в нем индуцируется ЭДС, положительное направление которой (см. рис. 29, а) связывают с положительным направлением потока Фх правилом буравчика.
Положительное направление ЭДС совпадает с направлением вращения рукоятки буравчика, ввинчивающегося в направлении магнитного потока Фх:
е = -dФх /dt = -Фт · ω ·cos (ω·t + ψФ) = Em sin (ω·t + ψe).
где Ет = - ω · Фт — амплитуда ЭДС; ω·t + ψe = α — начальная фаза ЭДС.
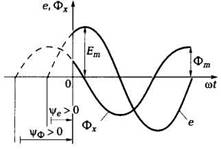
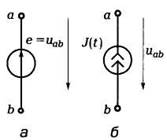
Рис. 30. Зависимости магнитного потока и ЭДС. Рис. 31 Источники напряжения и тока
На рис. 31 изображены зависимости магнитного потока Фх = Фх (ω·t) и ЭДС е = e (ω·t) от фазы ω·t, т.е. от времени t. Заметим, что синусоидальные величины принято изображать графиками в виде зависимостей от ω·t. Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат, т. е. ω·t= 0. Начальная фаза отсчитывается вдоль оси абсцисс от ближайшего к началу координат нулевого значения синусоидальной величины при ее переходе от отрицательных значений к положительным до начала координат.
Если начальная фаза больше (меньше) нуля, то начало синусоидальной величины сдвинуто влево — как на рис. 30 — (вправо) от начала координат.
Если к выводам а и b генератора подключить резистор сопротивлением нагрузки Rн (см. рис. 29, а), то в полученной цепи будет синусоидальный ток i.
На рис. 29, в приведена схема замещения электромеханического генератора, в которой резистивный Rвт и индуктивный Lвт элементы отображают внутренние параметры генератора: сопротивление проводов и собственную индуктивность витка. Если параметрами резистивного и индуктивного элементов в схеме замещения генератора можно пренебречь, то его схемой замещения будет идеальный источник синусоидальной ЭДС е или источник синусоидального напряжения (рис. 31, а). Второе определение идеального источника напряжения: идеальным источником напряжения называется источник, внутреннее сопротивление которого равно нулю. Если ток в цепи генератора не зависит от параметров внешней цепи, то схемой замещения генератора будет идеальный источник синусоидального тока J(t) (рис. 31, б), где J(t) = iк — ток генератора при коротком замыкании его выводов a и b. Второе определение идеального источника тока: идеальным источником тока называется источник, внутреннее сопротивление которого равно бесконечности.
Источники ЭДС и тока называются активными элементами, а резистивные, индуктивные и емкостные элементы — пассивными элементами схем замещения.
МАКСИМАЛЬНОЕ, СРЕДНЕЕ И ДЕЙСТВУЮЩЕЕ ЗНАЧЕНИЯ СИНУСОИДАЛЬНЫХ ВЕЛИЧИН
В линейной цепи при действии синусоидально изменяющейся ЭДС токи также синусоидальны:
i =Im·sin(ωt + ψi),
где ω — угловая частота; ψi — начальная фаза тока; Im — максимальное значение (амплитуда) тока.
Средним значением синусоидального тока считают его среднее значение за положительный полупериод, совпадающее со средним значением по модулю:
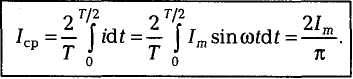
Если в резистивном элементе сопротивлением R при постоянном и синусоидальном токах за одинаковый интервал времени выделяется одинаковая энергия, то такое значение постоянного тока называется действующим значением соответствующего синусоидального тока.
За интервал времени один период Т в резистивном элементе сопротивлением R выделяется энергия при синусоидальном токе
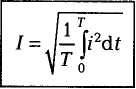
как среднее квадратичное за период. На рис. 4.4 показаны зависимости от времени синусоидального тока i, квадрата тока i 2 и графическое определение значения I2 (из равенства площадей
I2Т = 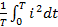 ,
,
а тем самым и действующего значения тока I.
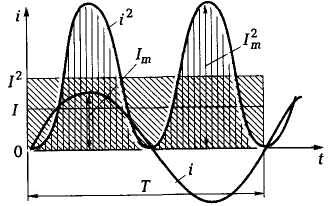
Рис.32.Зависимоть синусоидального тока и квадрата тока
Для синусоидального тока нетрудно определить действующее значение через амплитудное:
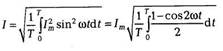
и так как 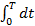 =T, а
=T, а 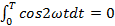 , то
, то
I=Im/√2
Аналогично для любой другой синусоидальной величины a=Am·sin(ωt+ψa) (ЭДС, напряжения, магнитного потока и т.д.) среднее и действующее значения равны
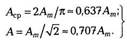
Известно несколько способов представления синусоидально изменяющихся величин: в виде тригонометрических функций, например, a=Am·sin(ωt+ψa.), графиков вращающихся векторов и комплексных чисел.
Представление синусоидальных величин вращающимися векторами.
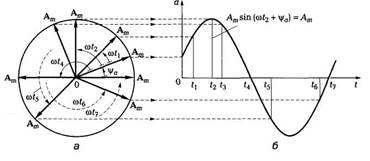
Рис.33
Для представления возьмём величину a=Am·sin(ωt+ψa) с начальной фазой ψa вращающимся вектором построим (рис. 4.5, а) радиус-вектор Аm этой величины длиной (в масштабе построения), равной амплитуде Ат, и под углом ψa к горизонтальной оси. Это будет его исходное положение в момент начала отсчета времени t = 0.
Если радиус-вектор вращать с постоянной угловой скоростью Ω, численно равной угловой частоте ω синусоидальной величины а, против направления движения часовой стрелки, то его проекция на вертикальную ось будет равна a=Am·sin(ωt+ψa). По значениям этих величин можно построить график зависимости синусоидальной величины от фазы cot или от времени t. Такое построение приведено для некоторых значений t на рис. 33, б.
Применение вращающихся векторов позволяет компактно представить на одном рисунке совокупность различных синусоидально изменяющихся величин одинаковой частоты.
Представление синусоидальных величин комплексными числами. От представления синусоидальных величин вращающимися радиусами-векторами нетрудно перейти к представлению синусоидальных величин комплексными числами.
Для того чтобы представить синусоидальную величину
a=Am·sin(ωt+ψa)
с начальной фазой ψa комплексным числом, проведем на комплексной плоскости (рис. 34) из начала координат под углом ψa к оси действительных величин против часовой (по часовой) стрелки, если значение угла ψa > 0 (ψa < 0) вектор, длина которого в масштабе построения равна амплитуде Ат синусоидальной величины. Конец этого вектора находится в точке, которой соответствует комплексное число — комплексная амплитуда синусоидальной величины:
a=Am·sin(ωt+ψa)
с начальной фазой ψa комплексным числом, проведём на комплексной плоскости (рис.34) из начала координат под углом к оси действительных величин против часовой (по часовой) стрелки, если значение угла ψa> 0 (ψa< 0) вектор, длина которого в масштабе построения равна амплитуде Am синусоидальной величины. Конец этого вектора находится в точке в точке, которой соответствует комплексное число – комплексная амплитуда синусоидальной величины:
Ǻт = Атejψa = Ат < ψa, где символ «<» означает не значение «меньше» а просто угол.
Так же обозначается и соответствующий комплексной амплитуде вектор на комплексной плоскости.
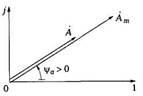
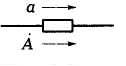
Рис. 34 Рис. 35
При увеличении во времени фазы синусоидальной величины угол ωt+ψa между осью и вектором растёт, а сам вектор будет представлять собой вращающийся вектор
Атej(ωt+ψa) =.
Нетрудно видеть, что мнимая часть вращающегося вектора равна заданной синусоидальной величине (4.7).
Представление синусоидальной величины комплексной амплитудой Ат и соответствующим ей вектором на комплексной плоскости геометрически подобно представлению той же синусоидальной величины вращающимся радиусом-вектором Ат в момент времени t = 0 (см. рис. 4.5, а). Поэтому может создаться впечатление, что оба представления синусоидальных величин практически совпадают. В действительности это не так. В случае представления синусоидальных величин комплексными числами можно применить эффективный комплексный метод анализа электрических цепей синусоидального тока, который в настоящее время завоевал всеобщее признание.
Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным действующим значением синусоидальной величины:
Ǻт = Ǻт/√2 = Атejψa = Ат < ψa, где символ «<» означает не значение «меньше» а просто угол.
Так же обозначается и сам вектор на комплексной плоскости (см. рис. 34).
Применяются три формы записи комплексного действующего значения синусоидальной величины:
■ показательная форма
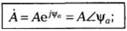
тригонометрическая форма
Ǻ = Am·cos ψa + Am ·sin ψa;
алгебраическая форма
Ǻ = ReǺ +jimǺ,
где ReǺ = Acos ψa и ImǺ = Asin ψa — действительная и мнимая составляющие комплексного действующего значении синусоидальной величины;
A=√((ReǺ)+(ImǺ)); ψa =arctg(ImǺ/ReǺ).
Переход от показательной формы к тригонометрической выполнен с помощью формулы Эйлера:
e± jψa = cosψa + sinψa.
При значениях угла ψa = π/2 и ψa = -π/2 следует:
e+ jπ/2 = J и e- jπ/2 = - J,
где j = √-1 — мнимая единица.
При анализе цепей синусоидального тока применяют комплексные действующие значения синусоидальных величин. Сокращенно их называют комплексными значениями, а соответствующие векторы на комплексной плоскости — векторами комплексных значений.
Совокупность векторов комплексных значений синусоидальных величин одной частоты называется векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов. Это упрощает расчеты и делает их наглядными.
Взаимное расположение векторов комплексных значений на векторной диаграмме не изменится, если начальные фазы ψa всех комплексных значений уменьшить (увеличить) на одну и ту же величину. Это означает лишь одновременный поворот всех векторов на один и тот же угол. Часто при анализе цепей векторную диаграмму строят так, чтобы вектор одного комплексного значения был направлен вдоль оси действительных величин. Такой вектор называется исходным вектором.
Его начальная фаза ψa = 0.
Направления синусоидальных величин (тока, напряжения и др.) в цепи периодически изменяются, но одно из двух направлений принимается положительным. Это направление выбирается произвольно и показывается стрелком на схеме соответствующего участка цепи. При выбранном положительном направлении синусоидальная величина представляется мгновенным значением а = Amsin (ωt+ψa) и соответствующим комплексным значением Ǻт = Ат < ψa. Следовательно, взаимно-однозначному представлению синусоидальных величин (токов, напряжений и Л|>) в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления.
Заметим, что в отличие от мгновенных значений синусоидальных величин соответствующие им комплексные значения не имеют размерностей.