ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ РАССУЖДЕНИЯ

 

1.45. Я пойду или в кино на новую кинокомедию (А), или на занятие по математической логике (В).Если я пойду в кино на новую кинокомедию, то я от всей души посмеюсь (С). Если я пойду на занятие по математической логике, то испы­таю большое удовольствие от следования по путям логиче­ских рассуждений (D). Следовательно, или я от всей души по­смеюсь, или испытаю большое удовольствие от следования по путям логических рассуждений.

Справедливо ли проведенное рассуждение?

Решение. Учитывая символические обозначения вы­сказываний, приведенные в условии, запишем посылки наше­го рассуждения:

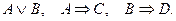
Покажем, что для формул алгебры высказываний имеет место следующее логическое следование:

├

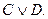
1.46. Если цех II не будет участвовать в выпуске нового образца продукции, то не будет участвовать и цех I. Если же цех II будет участвовать в выпуске нового образца, то в этой
работе непременно должны быть задействованы цеха I и III. Необходимо ли участие цеха III, если в выпуске нового образ­ца будет участвовать цех I?

1.47. Если Антон ляжет сегодня поздно, то утром он будет в нерабочем состоянии. Если он ляжет не поздно, то ему будет казаться, что он много времени теряет бесполезно. Следовательно, или Антон завтра будет в нерабочем состоянии, или ему будет казаться, что он много времени те­ряет напрасно.

Справедливо ли такое заключение?

1.48. Если я пойду завтра на первое занятие (А), то дол­жен буду рано встать (В), а если я пойду вечером на танцы (С), то лягу спать поздно (D). Если я лягу спать поздно и встану рано, то буду вынужден довольствоваться пятью ча­сами сна (Е). Я просто не в состоянии обойтись пятью часами сна. Следует ли отсюда, что я должен или пропустить завтра
первое занятие, или не ходить вечером на танцы?

Решение. Посылки нашего рассуждения можно запи­сать в следующем символическом виде: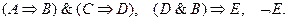

Нам нужно выяснить, вытекает ли отсюда утверждение 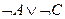. Предположим, что высказывание 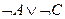ложно, в то время как все посылки истинны. Тогда 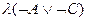= 0, т. е l(А)=1 и l(С)=1, в то время как

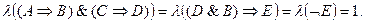
Из этих условий заключаем, что l(Е)=0, l(D & В) = 0. Следовательно, l(D) = 0 или l(В) = 0. Если l(D) = 0, то

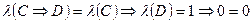и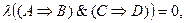

что противоречит предположению. Если же l(В) = 0, то аналогично

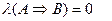и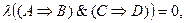

что снова противоречит предположению. Следовательно, не может быть ложно высказывание 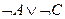, если все данные посылки истинны. Значит, вывод 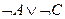верен.

1.49. Если завтра будет холодно, то я надену теплое пальто, если рукав будет починен. Завтра будет холодно, а рукав не будет починен. Следует ли отсюда, что я не надену теплое пальто?

1.50. Андрей или переутомился, или болен. Если он переутомился, то он раздражается. Он не раздражается. Следует ли отсюда, что он не болен?

1.51. Если 2 - простое число, то 2 – наименьшее простое число. Если 2 - наименьшее простое число, то 1 не является простым числом. Число 1 не является простым
числом. Следует ли отсюда, что 2 - наименьшее простое число? Следует ли отсюда, что 2 - простое число?

1.52. Если выиграет куйбышевский «Спартак», то Куйбышев будет торжествовать. Если же выиграет саратовский «Кристалл», то торжествовать будет Саратов. Выиграет или «Спартак», или «Кристалл». Однако если выиграет «Спартак», то Саратов не будет торжествовать, а если выиграет «Кристалл», то торжествовать не будет Куйбы­шев. Вытекает ли отсюда, что Куйбышев будет торжествовать тогда и только тогда, когда не будет торжествовать Саратов?

1.53. Или Анна и Антон одного возраста, или Анна старше Антона. Если Анна и Антон одного возраста, то На­таша и Антон не одного возраста. Если Анна старше Анто­на, то Антон старше Николая. Следует ли отсюда, что либо Наташа и Антон не одного возраста, либо Антон старше Ни­колая?

1.54. Если 6 - составное число, то 12 - составное число. Если 12 - составное число, то существует простое число больше чем 12. Если существует простое число боль­ше 12, то существует составное число больше 12. Если 6 делится на 2, то 6 - составное число. Число 12 составное. Следует ли отсюда, что 6 - составное число?

1.55. Если я поеду автобусом, а автобус опоздает, то я пропущу назначенное свидание. Если я пропущу на­значенное свидание и начну огорчаться, то мне не сле­дует ехать домой. Если я не получу работу, то я нач­ну огорчаться и мне следует поехать домой. Следует ли тогда, что если я поеду автобусом и автобус опоздает, то я получу работу?

1.56. Если Сергей выиграет теннисный турнир, то он будет доволен, а если он будет доволен, то он плохой борец в последующих турнирах. Но если он проиграет этот турнир, то потеряет поддержку своих болельщиков. Он плохой борец в последующих турнирах, если потеряет поддержку своих болельщиков. Если он плохой борец в по­следующих турнирах, то ему следует прекратить занятия тен­нисом. Сергей или выиграет этот турнир, или проиграет его. Следовательно, ему нужно прекратить занятия теннисом.

Справедливо ли приведенное рассуждение с точки зрения логики?

 

«ЛОГИЧЕСКИЕ» ЗАДАЧИ

 

1.57. Один из трех братьев Витя, Толя, Коля разбил окно. В разговоре участвуют еще двое братьев - Андрей и Дима.

- Это мог сделать только или Витя, или Толя, - сказал Андрей.

- Я окно не разбивал, - возразил Витя, - и Коля тоже.

- Вы оба говорите неправду, - заявил Толя.

- Нет, Толя, один из них сказал правду, а другой сказал неправду, - возразил Дима.

- Ты, Дима, неправ, - вмешался Коля.

Их отец, которому, конечно, можно доверять, уверен, что трое братьев сказали правду. Кто разбил окно?

Решение. Введем обозначения для высказываний:

В: «Витя разбил окно»;

Т: «Толя разбил окно»;

К: «Коля разбил окно».

Тогда высказывания братьев можно записать в символиче­ской форме следующим образом:

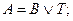
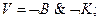
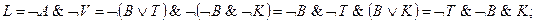
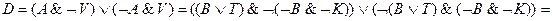
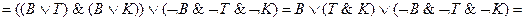
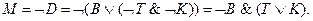
Образуем из высказываний А, V, L, D, М всевозможные конъюнкции по три высказывания: А&V&L, А&V&D, А&L&D, А&L&M, А&D&M, V&L&D, V&L&M, V&D&M, L&D&M Поскольку из выска­зываний А, V, L, D и М только три истинны, то из десяти конъюнкций истинна лишь одна. Проверьте самостоятельно, что конъюнкции A&L, V&L и L&D ложны, а поэтому восемь из перечисленных конъюнкций ложны. Остаются две конъюнкции: А& V&D и А&V&М. Рассмотрим их:

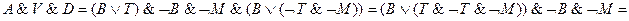=0;

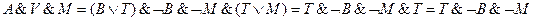
Итак, заключаем, что истинно высказывание Т&Ø В &Ø М, т. е. истинны высказывания Т, Ø В и Ø М. Следовательно, окно разбил Толя.

1.58. Один из трех братьев поставил на скатерть кляксу.

- Витя не ставил кляксу, - сказал Алеша. - Это сде­лал Боря.

- Ну, а ты что скажешь? - спросила бабушка Борю.

- Это Витя поставил кляксу, - сказал Боря. - А Але­ша не пачкал скатерть.

- Я знаю, что Боря не мог это сделать. А я сегодня не готовил уроки, - сказал Витя.

Оказалось, что двое мальчиков в каждом из двух случаев сказали правду, а один оба раза сказал неправду. Кто по­ставил на скатерть кляксу?

Указание. Образуйте сначала всевозможные попарные дизъюнк­ции из высказываний братьев. Все они будут истинны. Затем рассмотрите конъюнкцию всех этих истинных дизъюнкций. Она также будет истинна. Преобразовав ее к конъюнкции элементарных высказываний, установите виновного.

1.59. Один из четырех мальчиков испортил выключатель. На вопрос: «Кто это сделал?» — были получены такие отве­ты: 1) «Это сделал или Миша, или Коля»; 2) «Это сделал или Витя, или Коля»; 3) «Это не могли сделать ни Толя, ни Миша»; 4) «Это сделал или Витя, или Миша». Можно ли по этим дан­ным установить, кто виновен в поломке выключателя, если из четырех высказываний три высказывания истинны?

1.60. Четыре друга - Антонов (А), Вехов (В), Сомов (С), Деев (Д) - решили провести свой отпуск в четырех различ­ных городах - Москве, Ленинграде, Киеве и Ташкенте. В какой город должен поехать каждый из них, если имеются следующие ограничения:

Р) если А не едет в Москву, то С не едет в Ленинград;

Q) если В не едет ни в Москву, ни в Ташкент, то А едет в Москву;

R) если С не едет в Ташкент, то В едет в Киев;

S) если Д не едет в Москву, то В едет в Москву;

Т) если Д не едет в Ленинград, то В не едет в Москву?

Решение. Символом А_м обозначим высказывание; «Антонов едет в Москву», символом - А_м высказывание «Антонов не едет в Москву». Аналогичны буквенные обозна­чения и для других товарищей. Тогда ограничения ­ символиче­ски запишутся так:

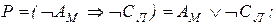
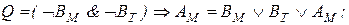
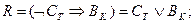
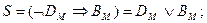
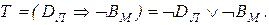
Составляем последовательно конъюнкции этих высказыва­ний. Каждая из них истинна:

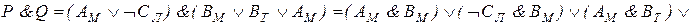
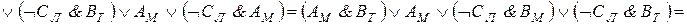
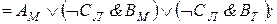
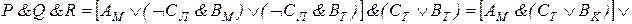
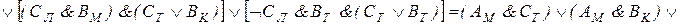
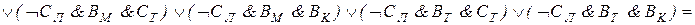
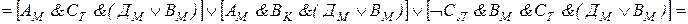
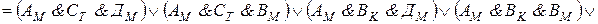
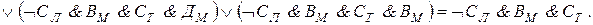
При проведении преобразований мы использовали тот факт, что ложными являются те конъюнкции, в которых го­ворится, что одно лицо поедет в два разных города или что два разных человека поедут в один город. Таким образом, мы установили, что конъюнкция 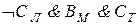истинна, т. е. истинны высказывания В_M и С_T. Далее, из условия Т и истин­ности В_M заключаем, что Д_л - истинно, т. е. Д_л ложно. Тогда истинно А_л. Следовательно, истинно Д_K. Итак, Анто­нов едет в Ленинград, Вехов - в Москву, Сомов - в Таш­кент, Деев - в Киев.

1.61. Шесть спортсменов - Адамов, Белов, Ветров, Гле­бов, Дронов, Ершов - в проходившем соревновании заняли шесть первых мест, причем ни одно место не было разделено между ними. О том, кто какое место занял, были получены такие высказывания: 1) «Кажется, первым был Адамов, а вторым - Дронов»; 2) «Нет, на первом месте был Ершов, а на втором - Глебов»; 3) «Вот так болельщики! Ведь Глебов был на третьем месте, а Белов - на четвертом»; 4) «И вовсе не так: Белов был пятым, а Адамов - вторым»; 5) «Вы все перепутали: пятым был Дронов, перед ним - Ветров». Изве­стно, что в высказывании каждого болельщика одно утвержде­ние истинное, а второе ложное. Определите, какое место занял каждый из спортсменов.

Указание. Рассмотрите высказывание; А_i: «Адамов занял i-е место» (i = 1, 2, 3, 4, 5, 6). Аналогичные значения имеют символы: В_i, V_i, G_i, D_i, E_i. Высказывания болельщиков представьте в виде дизъюнк­ций. Все они будут истинны. Рассмотрите конъюнкцию этих истинных дизъюнкций. Преобразуйте эту конъюнкцию и, учитывая ее истинность, выведите распределение мест между спортсменами.

1.62. Для четырех дружинников, фамилии которых начинаются буквами А, Е, Р, С, необходимо составить график де­журств на четыре вечера подряд, учитывая, что: 1) С и Р
не могут дежурить в первый вечер в связи с командировкой; 2) если С выйдет во второй вечер или Р - в третий то Е сможет подежурить в четвертый; 3) если А не будет дежурить
в третий вечер, то Е согласен дежурить во второй вечер; 4) если А или Р будут дежурить во второй вечер, то С сможет пойти в четвертый вечер; 5) если Р в четвертый вечер уедет на конференцию, то А придется дежурить в первый, а С - в третий вечер.

1.63. При составлении расписания уроков на один день учителя математики, истории и литературы высказали сле­дующие пожелания: математик просил поставить ему или
первый, или второй урок; историк - или первый, или третий; учитель литературы - или второй или третий. Как составить расписание уроков, чтобы учесть все пожелания?

1.64. Для полярной экспедиции из восьми претендентов А, В, С, D, E, F, G и H надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача..
Обязанности биолога могут выполнять Е и G, гидролога - В и F, синоптика - F и G, радиста - С и D, механика - С и H, врача - А и D. Хотя некоторые претенденты владеют
двумя специальностями, в экспедиции каждый сможет вы­полнять только одну обязанность. Кого и кем следует взять в экспедицию, если F не может ехать без В, D - без H и без
С, С не может ехать одновременно с G, а А не может ехать вместе с B?

1.65. Некий остров населен жителями, каждый из которых либо всегда говорит правду, либо всегда лжет и которые отвечают на вопросы только посредством «да» или «нет». К развилке дорог, из которых одна ведет в столицу острова, а другая туда не приводит, подходит путешественник. Никаких знаков, указывающих, какая из дорог куда ведет, у развилки нет. Но здесь стоит местный житель, некто N. Какой вопрос, предусматривающий ответ «да» или «нет», должен задать ему путешественник, чтобы определить, какая дорога ведет в столицу острова?

Решение. Пусть А обозначает высказывание: «N всегда говорит правду», а В обозначает высказывание: «Дорога, идущая налево, ведет в столицу». Построим такое со­ставное высказывание из высказываний А и В, чтобы ответ местного жителя на вопрос, истинно ли оно, гласил «да» тогда и только тогда, когда истинно высказывание В независимо от того, говорит ли местный житель всегда правду или всегда лжет.

Путешественнику достаточно спросить: «Верно ли, что N всегда говорит правду и дорога, идущая налево, ведет в столицу или что N всегда говорит неправду и дорога, идущая налево не ведет в столицу?», т. е. «Истинно ли высказывание 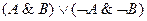?» Проверим, что из ответа «да» вне зависимости от того, говорит ли N правду или нет, следует, что дорога, идущая налево, ведет в столицу, а из ответа «нет» следует, что эта дорога не ведет в столицу. Здесь возможны 4 случая:

а) ответ «да», N говорит правду;

а) ответ «да», N лжет;

а) ответ «нет», N говорит правду;

а) ответ «нет», N лжет.

Рассмотрим, например, последний случай. Тогда

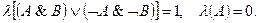
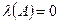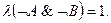Так как , то , и следовательно, И снова: так как 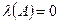, то 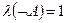, а значит 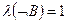. Отсюда 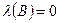. Итак, при ответе «нет» мы заключаем, что дорога, идущая налево, не ведет в столицу.

Оставшиеся три случая предполагается читателю аналогичным образом рассмотреть самостоятельно.

1.66. Три ученика различных школ города Новгорода приехали на отдых в один летний лагерь. На вопрос вожатого, в каких школах Новгорода они учатся, каждый дал ответ:

Петя: “Я учусь в школе №24, а Леня - в школе № 8”.

Леня: “Я учусь в школе №24, а Петя - в школе № 30”.

Коля: “Я учусь в школе №24, а Петя - в школе № 8”.

Вожатый, удивленный противоречиями в ответах ребят, попросил их объяснить, где правда, а где ложь. Тогда ребята признались, что в ответах каждого из них одно утверждение верно, а другое - ложно.

В какой школе учится каждый из мальчиков?

1.67 Четыре спортсменки: Аня, Валя, Галя и Даша — заняли первые четыре места в соревновании по гимнастике, причем никакие две из них не делили между собой эти места. На вопрос, какое место заняла каждая из спортсменок, трое болельщиков ответили:

1. Аня — второе место, а Даша — третье место.

2. Аня — первое место, а Валя — второе место.

3. Галя — второе место, а Даша — третье место.

Оказалось, что каждый из болельщиков ошибся один раз.

Какое место заняла каждая из спортсменок?

1.68 Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: “Любопытно, что один из нас блондин, другой - брюнет, третий - рыжий, но ни у кого цвет волос не соответствует фамилии”.

Какой цвет волос у каждого из друзей?

1.69 Три друга: Алеша, Боря и Володя - учатся в различных школах города Новгорода (в школах №1, 8, 30). Все они живут на различных улицах (улица Рогатица, улица Газон и улица Ломоносова). Причем один из них любит математику, второй - биологию, а третий - химию. Известно, что:

1. Алеша не живет на улице Рогатица, а Борис не живет на улице Газон.

2. Мальчик, живущий на улице Рогатица, не учится в школе №30.

3. Мальчик, живущий на улице Газон, учится в школе №1 и любит математику.

4. Володя учится в школе №30.

5. Ученик школы №8 не любит химию.

В какой школе учится каждый из друзей, на какой улице он живет и какой предмет любит?

1.70. В семье четверо детей. Им 5, 8, 13 и 15 лет. Детей зовут Аня, Боря, Вера и Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на три.

1.71. Четыре подруги пришли на каток каждая со своим братом. Они разбились на пары и начали кататься. Оказалось, что в каждой паре “кавалер” выше “дамы”, и никто не катается со своей сестрой. Самый высокий из компании - Юра Воробьев, следующий по росту - Андрей Егоров, потом Люся Егорова, Сережа Петров, Оля Петрова, Дима Крымов, Инна Крымова и Аня Воробьева. Кто с кем катается?

1.72. На улице, встав в кружок, беседуют четыре девочки: Аня, Валя, Надя и Галя.

1. Девочка в зеленом платье - не Аня и не Валя - стоит между девочкой в голубом платье и Надей.

2. Девочка в белом платье стоит между девочкой в розовом платье и Валей.

Какого цвета платье у каждой из девочек?

1.73. Как-то раз четыре товарища (Петя, Боря, Леша и Коля) пошли со своими сестрами (Светой, Наташей, Олей и Леной) на школьный новогодний бал.

Определите, кто чей брат и кто с кем танцевал во время первого танца, если:

1. Каждый из ребят не танцевал со своей сестрой.

2. Лена танцевала с Петей, а Светлана — с братом Наташи.

3. Оля танцевала с братом Светланы, Боря — с сестрой Алеши, а Алеша — с сестрой Пети.

1.74. Огород прекрасной садовницы Лилии расшалился. Стоило ей пойти на пляж заняться серфингом, как репа перемешалась с капустой, бобы - с морковью. Лилия составила карту, по которой можно было бы вспомнить, что и где было посажено, но карту стащили несносные мыши!

Посмотрим, что же можно теперь сделать, чтобы восстановить былое великолепие.

1. Большинство грядок — не шпинат и не капуста.

2. Моркови на две грядки больше, чем репы, а шпината — на две грядки больше, чем моркови.

3. Грядок с бобами меньше, чем с огурцами.

4. Капусты на одну грядку меньше, чем шпината.

5. Лилия не очень любит репу, по этому посадила ее всего лишь одну грядку.

1.75. По утрам пятеро друзей (Макс, Дора, Боб, Иван и Борис) встречаются за чашкой кофе. Один из них выпивает в день одну чашку кофе, другой - 4, третий - 5, четвертый - 6, пятый - 8, однако кто-то пьет кофе без сахара, другие кладут в свою чашку по 1, 2, 4, 6 кусочков сахара, и несколько человек пьют свой кофе с молоком. Ваша задача - выяснить, сколько чашек кофе выпивает за день каждый; сколько кусочков сахара он кладет в кофе, и кто пьет кофе с молоком, а кто - нет.

1. Иван кладет в кофе втрое больше кусочков сахара, чем тот, кто выпивает за день 4 чашки кофе.

2. Трое, включая того, кто кладет в кофе 4 кусочка сахара, пьют кофе без молока.

3. Боб выпивает только одну чашку кофе в день, пьет кофе без молока и без сахара.

4. Дора пьет кофе и с молоком, и с сахаром.

5. Макс, который пьет кофе без молока, кладет в него вдвое меньше кусочков сахара, чем тот, кто выпивает за день в двое больше него кофе.

6. Борис выпивает на 2 чашки кофе больше, чем Иван - но Иван кладет в кофе на два куска сахара больше, чем Борис.