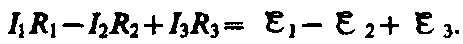среднее число столкновений

Средняя квадратная скорость

Средняя кинетическая энергия поступательного движения одной молекулы идеаль­ного газа

20. Применяя методы теории вероятностей. Максвелл нашел функцию f(v) — закон о распределения молекул идеального газа по скоростям:

Выражение называется распределением Больцмана для внешнего потенциаль­ного поля.

21. Средняя длина свободного пробега

среднее число столкновений

22. В термодинамически неравновесных системах возникают особые необратимые процес­сы, называемые явлениями переноса, в результате которых происходит пространствен­ный перенос энергии, массы, импульса. К явлениям переноса относятся теплопровод­ность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). Для простоты ограничимся одномер­ными явлениями переноса. Систему отсчета выберем так, чтобы ось х была ориен­тирована в направлении переноса.

Явление диффузии заключается в том, что происходит самопроиз­вольное проникновение и перемешивание частиц двух соприкасающихся газов, жид­костей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности.

Явление диффузии для химически однородного газа подчиняется закону Фука:

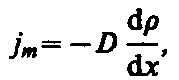
Согласно кинети­ческой теории газов,

23. Механизм возникновения внутреннего трения меж­ду параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

закону Ньютона:

Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле

Если в одной области газа средняя кинетическая энергия молекул больше,чем в другой, то с течением времени вследствие постоянных сто­лкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

подчиняется закону Фурье:

Теплопроводность l численно равна плотности теплового потока при градиенте температуры, равном единице.

24. внутренняя энергия U — энергия хаотического (теплового) движения микрочастиц системы (моле­кул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц.

внутренняя энергия, отнесенная к одному молю газа, будет равнасумме кинетических энергий N _a молекул:

Внутренняя энергия для произвольной массы т газа.

 

 

закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT.

средняя энергия молекулы

Удельная теплоемкость вещества — величина, равная количеству теплоты, необходи­мому для нагревания 1 кг вещества на 1 К:

Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг × К)).

25. Уравнение выражает первое начало термодинамики: теплота, сообщаемая систе­ме, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

Выражение в дифференциальной форме будет иметь вид

или в более корректной форме

Изохорный процесс (V =const)

Из первого начала термодинамики (dQ= d U+dA)дляизохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии:

Согласно формуле:

Тогда для произвольной массы газа получим

Изобарный процесс (p =const)

Если испо­льзовать уравнение Клапейрона — Менделеева для выбранных нами двух состояний, то

откуда

Тогда выражение для работы изобарного расширения примет вид

В изобарном процессе при сообщении газу массой т количества теплоты

его внутренняя энергия возрастает на величину

Изотермический процесс (T =const)

изотермический процесс описывается законом Бойля—Мариотта:

Так как при Т =const внутренняя энергия идеального газа не изменяется:

то из первого начала термодинамики (dQ= d U+dA) следует, что для изотермического процесса

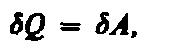
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:

26. Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ= 0)между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы.

Из первого начала термодинамики (dQ= d U+dA) для адиабатического процесса следует, что

т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Продифференцировав уравнение состояния для идеального газа получим

Исключим из уравнений температуру Т.

Разделив переменные и учитывая, что С_p/С_V=g, найдем

Интегрируя это уравнение в пределах от p ₁ до p ₂ и соответственно от V ₁ до V ₂, а затем потенцируя, придем к выражению

Так как состояния 1 и 2 выбраны произвольно, то можно записать

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

27. Работа газа при изохорном процессе

Работа газа при изобарном процессе

Работа изотермического расширения газа:

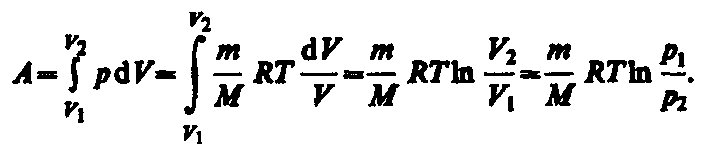
28. Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, будет необратимым.

29. Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S.

Неравенства Клаузиуса

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

30. второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Можно дать более краткую формулировку второго начала термодинамики: в про­цессах, происходящих в замкнутой системе, энтропия не убывает.

Укажем еще две формулировки второго начала термодинамики:

1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным результатом которо­го является передача теплоты от менее нагретого тела к более нагретому.

статистическое толкование: энтропия является мерой неупорядо­ченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом мак­симальна и энтропия.

31. Реальные газы — газы, свойства которых зависят от взаимо­действия молекул, надо учитывать силы межмолекулярного взаимодействия

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):

Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV _m, уравнение Ван-дер-Ваальса примет вид

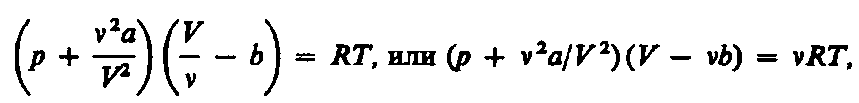
32. Изотермы Ван-дер-Ваальса — кривые зависимости р от V _m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые имеют довольно своеобразный характер. При высоких температурах (T > T _к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой.

Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул и потенциальной энергии межмолекулярного взаимодействия.

Внутренняя энергия моля реального газа

растет с повышением температуры и увеличением объема.

33. Изменение температуры реального газа в результате его адиабатического расшире­ния, или, как говорят, адиабатического дросселирования — медленного прохождения газа под действием перепада давления сквозь дроссель (например, пористую перегород­ку), называется эффектом Джоуля—Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (D T <0), и отрицательным, если газ нагревается (D T > 0).

Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности. В самом деле, для моля идеального газа рV _m =RТ, поэтому выражение примет вид

откуда следует, что Т ₁ = T ₂.

34. Элект­рические поля, которые создаются неподвижными электрическими зарядами и называ­ются электростатическими.

Закон Кулона:сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q ₁ и Q ₂ и обратно пропорциональна квадрату расстояния r между ними:

35. Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд — такой заряд, который не искажает исследу­емое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд Q ₀, то на него действует сила F, различная в разных точках поля, которая, согласно закону Кулона (78.2), пропорци­ональна пробному заряду Q ₀. Поэтому отношение F/ Q ₀ не зависит от Q ₀ и характеризу­ет электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатичес­кого поля.

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

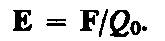
Напряженность поля точечного заряда в вакууме

Формула выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рассчитать электростатические поля любой си­стемы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Вектор электрического смещения, который для электрически изотроп­ной среды, по определению, равен

Вектор электрического смещения можно выразить как

36. Величина

называется потоком вектора напряженности через площадку d S.

Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e₀.

37. Работа при перемещении заряда Q ₀ из точки 1 в точку 2

Работа, совершаемая селами электростатического поля при перемещении заряда Q ₀ из точки 1 в точку 2, может быть представлена как

т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках.

Работа сил поля при перемещении заряда Q ₀ из точки 1 в точку 2 может быть записана также в виде

Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещен­ного в эту точку.

Из определения градиента следует, что

т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.

Связь между напряженностью и потенциалом

38. Под емкостью конденсатора понимается физическая величина, равная отноше­нию заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁ — j₂) между его обкладками:

для емкости плоского конденсатора:

для емкости цилиндрического конденсатора:

39. Диэлектрики (например, стекло, пластмассы) — тела, в которых практически отсутствуют свободные заряды.

40. Поляризацией диэлектрика называется процесс ориентации диполей или появления под воздействием внешнего электрического поля ориентированных по полю диполей.

Три вида поляризации:

1) электронная, или деформационная, поляризация диэлектрика с неполярными молеку­лами, заключающаяся в возникновении у атомов индуцированного дипольного момен­та за счет деформации электронных орбит;

2) ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю.

3) ионная поляризация диэлектриков с ионными кристаллическими решетками, заклю­чающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицатель­ных — против поля, приводящем к возникновению дипольных моментов.

Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Е_t) и нормальная составляющая вектора D (D_n) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора Е (E_n) и тангенциальная составляющая вектора D (D_t) претерпевают скачок.

41. Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т. е. поляризованностью в отсут­ствие внешнего электрического поля. К сегнетоэлектрикам относятся, например, дета­льно изученные И. В. Курчатовым (1903—1960) и П. П. Кобеко (1897—1954) сегнетова соль NaKC₄H₄O₆ • 4Н₂О (от нее и получили свое название сегнетоэлектрики) и титанат бария ВаТiO₃.

о пьезоэлектриках — кристаллических веществах, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация даже в отсутст­вие внешнего электрического поля (прямой пьезоэффект). Наблюдаетсяи обратный пьезоэффект — появление механической деформации под действием электрического поля.

42. Энергия конден­сатора выражается через величину, характеризующую электростатическое поле, — на­пряженность Е.

43. Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока

закон Ома в дифференциальном форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке.

закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

или

Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:

44. Закон Ома для замкнутой цепи:

ЗаконОма для замкнутой цепи будет иметь вид

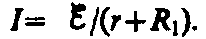
- э.д.с., действующая в цепи,

45. Не

46. Температурная зависимость сопротивления. Из формулы удельной проводимости следует, что сопротивление металлов, т. е. величина, обратно пропорциональ­ная g, должна возрастать пропорционально . Этот вывод электронной теории противоречит опытным данным, согласно которым R ~ T.

Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах T_K (0,14—20 К), называемых критическими, характерных для каждого вещества, скачко­образно уменьшается до нуля (кривая 2), т. е. металл становится абсолютным провод­ником. Впервые это явление, названное сверхпроводимостью. Явление сверхпроводимости объясняется на основе квантовой теории.

47. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

 

Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме э.д.с., встречающихся в этом контуре: