Методика выполнения работы

Цель работы

1. Рассмотреть постановку задачи.

2. Усвоить поиск допустимого решения.

3. Усвоить поиск оптимального решения, метод потенциалов.

4. Рассмотреть транспортные задачи с неправильным балансом.

5. Научиться находить вырожденное решение.

 

Теоретическое введение

Общая характеристика распределительной задачи

Распределительные задачи связаны с распределением ресурсов по работам, которые необходимо выполнить. Задачи этого класса возникают тогда, когда имеющихся в наличии ресурсов не хватает для выполнения каждой работы наиболее эффективным образом. Поэтому целью решения задачи является отыскание такого распределения ресурсов по работам, при котором либо минимизируются общие затраты, связанные с выполнением работ, либо максимизируется получаемый в результате общий доход.

Большинство распределительных задач можно представить в виде матриц, приведенных в таблице 3.1.

Элементы Cij, стоящие в клетках матрицы, соответствуют затратам или доходу, отвечающим выделению, одной единицы ресурса Ri на работу Jj. Величины Cij могут быть зависимыми и независимыми.

Так, например, затраты, обусловленные назначением одной автомашины на некоторый маршрут доставки грузов, не зависят от того какие машины назначены на обслуживание других маршрутов. В то же время при распределении разделением (скажем производством) обычно зависит от того, какие средства будут затрачены другими подразделениями (скажем отделом сбыта). В теории распределения рассматриваются преимущественно задачи с независимыми затратами и доходами. Это объясняется не тем, что такие задачи более важны, а лишь тем, что для них значительно легче строить модели и получать решения.

Если затраты (или доход), определяемые объемом Хij ресурса I, выделенного на выполнение работы Ji, равны ХijCij, то имеем линейную распределительную задачу.

Основные методы решения распределительных задач, в частности линейного программирования, построены на допущении, что объемы, имеющихся в наличии ресурсов (bi), требуемые объемы (aj) и затраты (Ci,j) точно известны.

Если общий объем наличных ресурсов Σb_i (i = 1…m) равен общей потребности в них Σa_j (i =1…n), то имеет место сбалансированная (закрытая) распределительная задача. Если же Σa_j ≠ Σb_i, то задача называется несбалансированной (открытой). Если ресурсы можно разделить между работами, то некоторые работы можно выполнять с помощью различных комбинаций ресурсов. Если работы и ресурсы измеряются в единицах одной и той же шкалы, то такие задачи обычно называют транспортными или задачами разложения. Если же работы и ресурсы выражаются в различных единицах измерения, то задача называется общей разделительной задачей. Таким образом, транспортная задача является частным случаем общей распределительной задачи.

Таблица 3.1.

 

Методика выполнения работы

3.2.2.1 Транспортная задача

Имеется М поставщиков некоторого товара. Количество товара, имеющееся у поставщиков, составляет А₁, А₂,…, А_М единиц. Имеются N потребителей этого товара; их спрос составляет B₁, B₂, …, B_N единиц. Сумма запасов товара, имеющихся у поставщиков, равна сумме величин спроса всех потребителей:

Известны затраты на перевозку единицы товара от каждого поставщика каждому потребителю (стоимости перевозок): C_ij, i =1, …, M, j =1, …, N.

Требуется составить такой план перевозок (откуда, куда и сколько единиц поставить), чтобы все заявки были выполнены, а общая стоимость всех перевозок была минимальна.

Рассмотрим сначала решение закрытой транспортной задачи, т.е. когда сумма всех заявок равна сумме всех запасов.

Пояснить его проще всего будет на конкретном примере:

Пример 3.1. С четырех складов (СК1, СК2, СК3, СК4) доставляется товар в три магазина (МГ1, МГ2, МГ3). На складе СК1 имеется 40 тонн товара, на складе СК2 – 50 тонн, на складе СК3 – 60 тонн, на складе СК4 – 30 тонн. Магазину МГ1 требуется 60 тонн товара, магазину МГ2 – 80 тонн, магазину МГ3 – 40 тонн. Затраты (в ден. ед.), связанные с перевозкой одной тонны товара с каждого склада в каждый магазин, приведены в табл. 3.2.

Таблица 3.2

Склады	Магазины
МГ1	МГ2	МГ3
СК1
СК2
СК3
СК4

 

Требуется определить, сколько товара необходимо перевезти с каждого склада в каждый магазин, чтобы доставить всем магазинам необходимое количество товара с минимальными затратами.

Данную задачу можно представить как задачу линейного программирования. Для построения математической модели этой задачи введем переменные X_ij, i =1,…,4, j=1,…,3, обозначающие количество товара, перевозимого с i-го склада в j-й магазин.

На складах имеется 180 единиц товара; магазинам требуется также 180 единиц товара. Поэтому для удовлетворения спроса всех магазинов потребуется вывезти со складов весь товар. Ограничения, выражающие это требование, имеют следующий вид:

 

x₁₁ + x₁₂ + x₁₃ = 40

x₂₁ + x₂₂ + x₂₃ = 50

x₃₁ + x₃₂+ x₃₃ = 60

x₄₁ + x₄₂ + x₄₃= 30.

 

Каждый магазин должен получить ровно столько товара, сколько ему требуется. Ограничения, выражающие это условие, следующие:

 

x₁₁ + x₂₁ + x₃₁+ x₄₁= 60

x₁₂ + x₂₂+ x₃₂ + x₄₂= 80

x₁₃ + x₂₃ + x₃₃ + x₄₃= 40.

 

Так как переменные обозначают количество перевозимого товара, на них накладывается требование неотрицательности:

x _ij³0, i =1,…,4, j=1,…,3.

Целевая функция представляет собой затраты на выполнение всех перевозок:

Е = 4x₁₁ + 3x₁₂+ 5x₁₃ + 6x₂₁ + 2x₂₂ + 1x₂₃ + 10x₃₁ + 4x₃₂+ 7x₃₃ + 8x₄₁ + 6x₄₂ + +3x₄₃ ® min.

Такую задачу можно решить симплекс-методом, как и любую задачу линейного программирования. Однако такое решение окажется достаточно сложным из-за большого количества переменных и ограничений, входящих в математическую модель задачи. Для решения задач такого вида существуют специальные, более простые методы.

При решении транспортной задачи удобно пользоваться расчетной таблицей, содержащей стоимости перевозок, запасы товара у поставщиков и величины спроса потребителей. По ходу решения задачи в нее заносятся величины перевозок (значения переменных x_ij), а также вспомогательные величины, используемые для решения задачи. Расчетная таблица для примера 5.1 показана в табл 3.3.

 

Таблица 3.3

Склады	Магазины
МГ1	МГ2	МГ3
СК1
СК2
СК3
СК4

 

Решение транспортной задачи включает два этапа:

· поиск допустимого решения, т.е. плана перевозок, при котором каждый потребитель получит весь необходимый товар, однако затраты на такие перевозки могут не быть минимальными;

· поиск оптимального решения, т.е. плана перевозок и минимальными затратами.

 

3.2.2.2 Поиск допустимого решения методом минимального элемента

Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ северо-западного угла, способ минимальной стоимости по строке, способ минимальной стоимости по столбцу и способ минимальной стоимости таблицы.

Рассмотрим поиск допустимого решения на основе метода минимального элемента. Принцип работы этого метода состоит в том, что в первую очередь планируются перевозки, требующие минимальных затрат.

Метод минимального элемента реализуется следующим образом. Выбирается минимальная стоимость перевозки единицы груза, т.е. минимальный из коэффициентов целевой функции C_ij, i =1, …, M, j =1, …, N. Если запас i -го поставщика превосходит спрос j-го потребителя (А i ³ В j), то спрос j-го потребителя полностью удовлетворяется за счет перевозок от i -го поставщика: Х ij = В j. При этом запас i -го поставщика уменьшается на величину В j (А i = А i – В j), а j-й потребитель исключается из дальнейшего рассмотрения, так как он уже получил необходимое количество товара (j-й столбец вычеркивается из расчетной таблицы). Если наоборот, спрос j-го потребителя превосходит запас, имеющийся у i -го поставщика (А i £ В j), то i -й поставщик перевозит весь имеющийся у него товар j-му потребителю: Х ij = А i. При этом спрос j-го потребителя уменьшается на величину А i (В j = В j– А i), а i -й поставщик исключается из дальнейшего рассмотрения (i -я строка вычеркивается из расчетной таблицы). В сокращенной расчетной таблице снова выбирается минимальная стоимость перевозок, и выполняются действия, аналогичные рассмотренным выше. Процесс продолжается, пока не будут распределены все запасы и удовлетворены все потребности.

Примечание. Если запас i -го поставщика оказывается равным спросу j-го потребителя (А i = В j), то из рассмотрения исключается или поставщик, или потребитель (но не оба вместе). Если исключается поставщик, то предполагается, что неудовлетворенный спрос потребителя составляет 0 единиц товара. Если исключается потребитель, то предполагается, что у поставщика остается запас в размере 0 единиц. Дальнейшие действия выполняются обычным образом согласно алгоритму метода минимального элемента. Подробнее такой случай рассмотрен в подразделе 3.5.

Рассмотрим поиск допустимого плана для примера 3.1. Наиболее дешевыми являются перевозки от второго поставщика третьему потребителю, т.е. со склада СК2 в магазин МГ3. Запас товара на складе СК2 составляет 50 тонн, а спрос магазина МГ3 - 40 тонн. Поэтому склад СКl поставляет магазину МГЗ 40 тонн товара. Запас товара на складе СК1 уменьшается на 40 тонн (на складе остается 10 тонн), а магазин МГЗ исключается из рассмотрения, так как для него уже запланирована перевозка необходимого количества товара (табл. 3.4.)

В сокращенной расчетной таблице (см. табл. 5.4) выбирается минимальный элемент. Наиболее дешевыми являются перевозки со склада СК2 в магазин МГ2. Запас товара на складе составляет 10 тонн (так как для этого склада уже запланирована перевозка 40 тонн товара в магазин МГЗ), а спрос магазина – 80 тонн. Поэтому склад СК2 поставляет магазину МГ2 весь имеющийся у него товар. Склад СК2 исключается из рассмотрения, а спрос магазина МГ2 уменьшается на 10 тонн (табл. 3.5 ).

 

Таблица 3.4 Таблица 3.5

В сокращенной расчетной таблице (см. табл. 3.5) минимальную стоимость имеют перевозки со склада СК1 в магазин МГ2. Запас товара на складе СК1 составляет 40 тонн, а спрос магазина МГ2 – 70 тонн (так как для этого магазина уже запланирована перевозка 10 тонн товара со склада СК2). Поэтому СК1 поставляет магазину МГ2 весь имеющийся у него товар. Склад СК1 исключается из рассмотрения, а спрос магазина МГ2 уменьшается на 40 тонн (табл. 3.6).

В сокращенной расчетной таблице (см. табл. 3.6) наиболее дешевыми являются перевозки со склада СК3 в магазин МГ2. Запас товара на складе СК3 составляет 60 тонн, а спрос магазина МГ2 – 30 тонн. Поэтому склад СК3 поставляет магазину МГ2 30 тонн товара. Запас товара на складе СК3 уменьшается на 30 тонн (на складе остается еще 30 тонн), а магазин МГ2 исключается из рассмотрения, так как для него уже запланирована перевозка необходимого количества товара (табл. 3.7).

 

Таблица 3.6 Таблица 3.7

 

В сокращенной расчетной таблице (см. табл. 3.7) минимальный элемент соответствует перевозкам со склада СК4 в магазин МГ1. Запас товара на складе СК4 составляет 30 тонн, а спрос магазина МГ1 – 60 тонн. Поэтому склад СК4 поставляет магазину МГ1 весь имеющийся у него товар. Склад СК4 исключается из рассмотрения, а спрос магазина МГ1 уменьшается на 30 тонн (табл. 3.8).

Запас товара (30 тонн) остается только на складе СК3. Такое количество товара требуется магазину МГ1 (для всех остальных магазинов уже запланированы необходимые перевозки). Поэтому склад СК3 поставляет магазину МГ1 30 тонн товара. На этом поиск допустимого решения завершается.

Таблица 3.8 Таблица 3.9

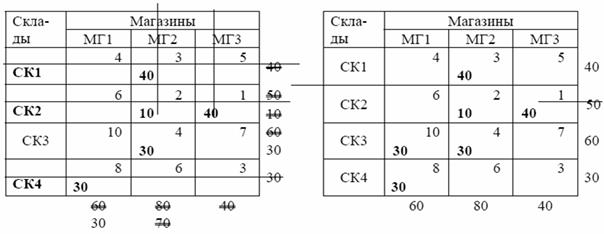
Полученный допустимый план перевозок приведен в табл. 3.9. Склад СК1 поставляет 40 тонн товара магазину МГ2; склад СК2 поставляет 10 тонн товара магазину МГ2 и 40 тонн – магазину МГ3; склад СК3 поставляет 30 тонн товара магазину МГ1 и 30 тонн – магазину МГ2; склад СК4 поставляет 30 тонн товара магазину МГ1.

Другими словами, переменные приняли следующие значения:

x₁₂ =40, x₂₂ =10, x₂₃ =40, x₃₁ =30, x₃₂ =30, x₄₁ =30; остальные переменные равны нулю. Общие затраты на перевозки составят 840 ден. ед.

Переменные, принявшие ненулевые значения, называются базисными, остальные (нулевые) – небазисными.

Если допустимый план перевозок составлен правильно, то количество базисных переменных всегда равно M+N-1, где М– количество поставщиков, N – количество потребителей.

Примечание. Иногда некоторые из базисных переменных тоже принимают нулевые значения (см. подраздел 3.5). Однако количество базисных переменных всегда должно быть равно M+N-1.

 

3.2.2.3 Поиск оптимального решения. Метод потенциалов

Оптимальное решение (план перевозок с минимальной стоимостью) определяется методом потенциалов на основе допустимого решения, полученного каким-либо из указанных выше способов. Общий вид расчетной таблицы, используемой при поиске оптимального решения на основе метода потенциалов, показан в табл. 3.10.

 

Таблица 3.10

Смысл обозначений Ui, Vj, Cij и т.д. будет показан ниже.

Рассмотрим поиск оптимального решения для примера 3.1.

1. Составляются уравнения для определения вспомогательных величин Ui и Vj, i=1, …, М, j= 1, …, N:

Ui + Vj = Cij, (3.1)

 

где Cij – стоимости перевозок, соответствующие базисным переменным.

Количество таких уравнений равно М+ N –1 (т.е. равно количеству базисных переменных). Величины Ui называются платежами (или потенциалами) поставщиков,а Vj – платежами (потенциалами) потребителей.

Система уравнений (3.1) для рассматриваемого примера имеет следующий вид:

U₁ + V₂=3

U₂ + V₂=2

U₂ + V₃=1

U₃ + V₁=10

U₃+ V₂=4

U₄ + V₁=8.

 

2. Из системы уравнений (3.1) определяются платежи. Так как количество неизвестных (платежей) равно М+ N, а система состоит из М+ N –1 уравнения, один из платежей (обычно U₁) принимается равным нулю.

Найдем платежи для рассматриваемого примера. Пусть U₁=0. Тогда V₂=3 (из первого уравнения). По значению V₂=3 из второго уравнения получим U₂ =–1. Из третьего уравнения найдем V₃=2. Из пятого уравнения по значению V₂=3 получим U₃=1. продолжая расчеты аналогичным образом, получим: V₁=9, U₄=–1 (платежи указаны в порядке их вычисления). Для дальнейших расчетов удобно указать значения платежей возле соответствующих строк и столбцов расчетной таблицы (см. табл. 3.10, 3.11).

3. Для всех небазисных переменных находятся суммы платежей (псевдостоимости). Например, С’₁₁ = U₁ + V₁=9, С’₁₃ = U₁ + V₃=2, и т.д. Псевдостоимости удобно вычислять по расчетной таблице. Эти величины также следует занести в расчетную таблицу. В табл. 3.11 они указаны в левых верхних углах ячеек.

4. Для всех небазисных переменных находятся разности стоимостей и псевдостоимостей: D_ij = С_ij – С’_{ij .} Например, D₁₁ = С₁₁–С’₁₁= –5, D₁₃ = С₁₃–С’₁₃= 3, и т.д. В табл. 3.11 они указаны в правых нижних углах ячеек.

5. Если для всех D_ij выполняется условие D_ij ³0, то оптимальное решение найдено, и решение задачи завершается. Если имеются величины D_ij £0, то выполняется следующий шаг.

6. Определяется переменная для включения в базис. В качестве такой переменной выбирается переменная, которой соответствует максимальная по модулю отрицательная величина D_{ij .} Включение переменной Х _ij в базис означает, что должны выполняться перевозки от i -го поставщика к j-му потребителю. Соответствующая ячейка расчетной таблицы обозначается знаком «плюс».

В рассматриваемом примере имеются две отрицательные величины D_ij: D₁₁ = –5и D₂₁ = –2. Максимальная по модулю из этих величин D₁₁. Значит, для включения в базис выбирается переменная Х ₁₁.

Примечание. Если имеется несколько максимальных по модулю отрицательных величин D_ij (равных между собой), то для включения в базис можно выбирать любую из соответствующих переменных.

7. Определяется переменная для исключения и базиса. Для этого строится цикл.

Рассмотрим построение цикла для примера 3.1. Включение в базис переменной x₁₁означает, что будут выполняться перевозки товара со склада СК1 в магазин МГ1. Так как запас товара на складе СК1 ограничен (составляет только 40 тонн), потребуется снизить поставки магазину МГ2, т.е. переменную x₁₂. Для того чтобы магазин МГ2 получил необходимое количество товара (80 тонн), необходимо, чтобы какой-нибудь из складов, уже поставляющих товар этому магазину, увеличил свои поставки. Магазину МГ2 поставляют товар два склада: СК2 и СК3. Однако СК2 не может увеличить поставки магазину МГ3, а этот магазин получает весь необходимый товар (40 тонн) только со склада СК2. Поэтому поставки магазину МГ2 увеличивает склад СК3 (переменная Х ₃₂ увеличивается). Так как запас товара на складе СК3 ограничен, из-за увеличения поставок магазину МГ2 этот склад должен уменьшить поставки какому-либо другому магазину, в данном случае – магазину МГ1 (переменная x₃₁уменьшается). Для того чтобы магазин МГ1 получил необходимое количество товара, поставки в этот магазин будет выполнять склад СК1. Таким образом, цикл построен. Переменные, которые требуется увеличить, обозначаются знаком «плюс», а уменьшаемые – знаком «минус». Цикл показан в табл. 3.11.

Примечание. Если в расчетной таблице оказалась хотя бы одна величина D_ij £0, то всегда можно построить цикл, причем только один.

 

Таблица 3.11

 

Минимальная из переменных, отмеченная знаком «минус», исключается из базиса. Обозначим эту переменную как x _rs. В данном случае это переменная x₃₁. Исключение переменной x _rs из базиса означает, что перевозки от r-го поставщика s-му потребителю прекращаются.

Примечание. Если несколько переменных, отмеченных знаком «минус», имеют одинаковое минимальное значение, то для исключения из базиса выбирается любая из них.

8. Определяются новые значения базисных переменных (новый план перевозок). Все переменные, отмеченные знаком «плюс», увеличиваются на x _rs, а отмеченные знаком «минус» – уменьшаются на эту же величину. Значения остальных переменных не изменяются.

В данном примере x _rs = x₃₁ =30 (таким образом, перевозки со склада СК3 в магазин МГ1 выполняться не будут). Переменные, отмеченные в цикле знаком «плюс», увеличиваются на 30; это значит, что соответствующие перевозки увеличиваются на 30 тонн. Переменные, отмеченные знаком «минус», уменьшаются на 30. Новый план перевозок показан в табл. 5.12. Умножив величины перевозок (x _ij) на соответствующие стоимости перевозки единицы груза (С _ij), найдем целевую функцию: Е=690. Таким образом, в результате перехода к новому решению затраты на перевозки снизились.

Примечание. Если несколько переменных принимают нулевые значения, то из базиса исключается только одна из них – переменная x _rs, выбранная на шаге 7. Остальные переменные остаются базисными, хотя и имеют нулевые значения. Подробнее такой случай рассмотрен в подразделе 5.5.

9. Выполняется возврат к шагу 1.

Продолжим поиск оптимального решения для примера 3.1. Для нового базиса составим систему уравнений (3.1), чтобы определить платежи:

 

U₁ + V₁=4

U₁ + V₂=3

U₂ + V₂=2

U₂ + V₃=1

U₃+ V₂=4

U₄ + V₁=8.

 

Принимая U₁ =0, найдем остальные платежи: V₁ =4, V₂ =3, U₂ = –1, V₃ =2, U₃ =1, U₄ =4 (платежи указаны в порядке их вычисления). Затем определяются значения псевдостоимостей, далее – разности стоимостей и псевдостоимостей. Все эти величины приведены в табл. 3.12.

В таблице имеются отрицательные разности стоимостей и псевдостоимостей: это величины D₄₂ = –1и D₄₃ = –3. Это означает, что полученное решение не является оптимальным. Переменная x₄₃включается в базис. Для определения переменной, исключаемой из базиса, строится цикл.

 

Таблица 3.12

 

Включение в базис переменной x₄₃означает, что будут выполняться перевозки товара со склада СК4 в магазин МГ3. Поэтому потребуется уменьшить перевозки со склада СК4 какому-либо магазину (так как запас товара на складе ограничен). В данном случае можно уменьшить только поставки магазину МГ1. Чтобы магазин МГ1 получил необходимое количество товара, требуется увеличение поставок со склада СК1, т.е. увеличение переменной x₁₁. Из-за увеличения поставок магазину МГ1 склад СК1 должен уменьшить поставки магазину МГ2 (уменьшается переменная x₁₂). Чтобы магазин МГ2 получил необходимое количество товара, нужно, чтобы какой-либо из складов, уже поставляющих товар этому магазину, увеличил свои поставки. Магазину МГ2 поставляют товар склады СК2 и СК3; однако склад СК3 не может увеличить свои поставки, так как он поставляет магазину МГ2 весь имеющийся у него товар (60 тонн). Поэтому поставки магазину МГ2 увеличивает склад СК2 (увеличивается переменная x₂₂). Из-за этого склад СК2 должен снизить поставки магазину МГ3 (уменьшается переменная x₂₃). Для того чтобы магазин МГ3 получил необходимое количество товара, поставки в этот магазин будет выполнять склад СК4 (переменная x₄₃включается в базис). Таким образом, цикл построен (см. табл. 3.12).

Из базиса исключается переменная x₁₂=10, так как эта переменная – минимальная из отмеченных знаком «минус». Это значит, что перевозки со склада СК1 в магазин МГ2 выполняться не будут.

Определяется новый план перевозок: переменные, отмеченные знаком «плюс» увеличиваются на x _rs = x₁₂=10, а отмеченные знаком «минус» – уменьшаются на 10. Новый план перевозок показан в табл. 3.13. Целевая функция (стоимость всех перевозок) для этого плана равна Е=660 ден. ед

 

Таблица 3.13

 

Для полученного плана перевозок составим систему уравнений (3.1), чтобы определить платежи:

U₁ + V₁=4

U₂ + V₂=2

U₂ + V₃=1

U₃+ V₂=4

U₄ + V₁=8.

U₄+ V₃=3

 

В табл. 3.14 приведены платежи (Ui + Vj), псевдостоимости (С’_ij), разности стоимостей и псевдостоимостей (D_ij). Все величины D_ij неотрицательны. Это означает, что полученное решение оптимально.

 

Таблица 3.14

 

Таким образом, оптимальный план перевозок состоит в следующем. Склад СК1 поставляет 40 тонн товара магазину МГ1; склад СК2 поставляет 20 тонн товара магазину МГ2 и 30 тонн – магазину МГ3; склад СК3 поставляет 60 тонн товара магазину МГ2; склад СК4 поставляет 20 тонн товара магазину МГ1 и 10 тонн – магазину МГ3. Другими словами, переменные приняли следующие значения:

x₁₁ =40, x₂₂ =20, x₂₃ =30, x₃₂ =60, x₄₁ =20, x₄₃ =10; остальные переменные равны нулю. Общие затраты на перевозки составят 660 ден.ед.

 

3.2.2.4 Транспортные задачи с неправильным балансом

В предыдущих случаях мы рассматривали только такую задачу о перевозках, в которой сумма запасов ровна сумме заявок:

, (где i=1,...,m; j=1,...,n) (3.4.1)

Это классическая транспортная задача, иначе называемая, транспортной задачей с правильным балансом. Встречаются такие варианты транспортной задачи, где условие (3.4.1) нарушено. В этих случаях говорят о транспортной задаче с неправильным балансом.

Транспортные задачи с неправильным балансом – это задачи, в которых сумма запасов товара, имеющихся у поставщиков, не равна сумме величин спроса потребителей.

Все методы решения транспортных задач предназначены для задач с правильным балансом. Поэтому для решения задачи с неправильным балансом ее необходимо привести к правильному балансу, т.е. преобразовать в обычную транспортную задачу с правильным балансом. Способы такого преобразования зависят от постановки задачи. Полученная задача с правильным балансом решается обычными методами, как показано выше.

Баланс транспортной задачи может нарушаться в 2-х направлениях:

1. Сумма запасов в пунктах отправления превышает сумму поданных заявок

, (где i=1,...,m; j=1,...,n)

2. Сумма поданных заявок превышает наличные запасы

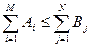, (где i=1,...,m; j=1,...,n)

Условимся первый случай называть “Транспортной задачей с избытком запасов“, а второй — “Транспортной задачей с избытком заявок”.

Рассмотрим последовательно эти два случая:

 

3.2.2.4.1 Транспортная задача с избытком запасов

В пунктах СК₁, СК_2, …СК_м имеются запасы груза A₁, A₂,..., A_m; пункты МГ₁, МГ₂, …, МГ_N подали заявки B₁, B₂,..., B_n, причем

, (где i=1,...,m; j=1,...,n)

Требуется найти такой план перевозок (X), при котором все заявки будут выполнены, а общая стоимость перевозок минимальна.

Очевидно, при этой постановке задачи некоторые условия-равенства транспортной задачи превращаются в условия-неравенства, а некоторые — остаются равенствами.

_n

∑X_i,j ≤ А_i (i=1,..., m);

^j=1

_M

∑ X_i,j = В_j (j=1,..., n).

ⁱ⁼¹

Мы умеем решать задачу линейного программирования, в какой бы форме — равенств или неравенств не были бы заданы ее условия. Поставленная задача может быть решена, например, обычным симплекс-методом. Однако задачу можно решить проще, если искусственным приемом свести ее к ранее рассмотренной транспортной задаче с правильным балансом. Для этого, сверх имеющихся n пунктов назначения МГ₁, МГ₂, …, МГ_N, введём ещё один, фиктивный, пункт назначения МГ_N+1, которому припишем фиктивную заявку, равную избытку запасов над заявками:

 

(где i=1,...,m; j=1,...,n),

 

а стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения МГ_N+1 будем считать равным нулю. Введением фиктивного пункта назначения МГ _N+1 с его заявкой МГ _N+1 мы сравняли баланс транспортной задачи и теперь его можно решать как обычную транспортную задачу с правильным балансом.

Если требуется обеспечить вывоз всего товара у какого-либо поставщика, то стоимость перевозки товара от этого поставщика фиктивному потребителю принимается равной очень большому числу.

Если требуется распределить излишек товара по всем поставщикам, то запасы товара у всех поставщиков искусственно уменьшаются. Для этого необходимо умножить все величины запасов на коэффициент . Вводить фиктивного потребителя в этом случае не требуется.

 

3.2.2.4.2 Транспортная задача с избытком заявок

Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления СК_М+1 с запасом А_М+1 равным недостающему запасу и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равным нулю.

Рассмотрим это на примере.

Пример 3.2. Пусть в условиях примера 3.1 на складе СК3 имеется только 45 тонн товара. Требуется составить план перевозок, при котором затраты на их выполнение будут минимальными.

В данной задаче сумма запасов товара на складах составляет 165 тонн, а потребности магазинов – 180 тонн. Поэтому при любом решении некоторые магазины получат меньше товара, чем им требуется. Задача состоит только в минимизации затрат на доставку имеющегося товара (165 тонн).

Для приведения этой задачи к правильному балансу необходимо добавить фиктивного поставщика. Его запас принимается равным разности между фактическими запасами, имеющимися на складах и потребностями магазинов, т.е. 15 тонн. Обозначим фиктивный склад СК5. Стоимости перевозки единицы товара с этого склада в любой магазин будем считать равными нулю. Расчетная таблица для этой задачи показана в табл. 3.15.

Таким образом, получена задача с правильным балансом. Она решается так же, как обычная транспортная задача.

Сначала требуется найти допустимый план перевозок. Найдем его с помощью метода минимального элемента. Полученный допустимый план приведен в табл. 3.16. Значение целевой функции (стоимость перевозок) для этого плана составляет 690 ден.ед.

На основе допустимого плана перевозок определяется оптимальный план. Для этого используем метод потенциалов. Оптимальный план приведен в табл. 3.17.

 

Таблица 3.15 Таблица 3.16

 

Таблица 3.17

 

Оптимальный план перевозок состоит в следующем. Склад СК1 поставляет 40 тонн товара магазину МГ1; склад СК2 поставляет 35 тонн товара магазину МГ2 и 15 тонн – магазину МГ3; склад СК3 поставляет 45 тонн товара магазину МГ2; склад СК4 поставляет 5 тонн товара магазину МГ1 и 25 тонн – магазину МГ3. Поставки с фиктивного склада, вошедшие в оптимальный базис, означают, что соответствующим потребителям будет поставлено меньше товара, чем им требуется. Таким образом, магазину МГ1 будет поставлено на 15 тонн товара меньше, чем ему требуется (т.е. всего 45 тонн вместо 60 необходимых). Общие затраты на перевозки составят 540 ден.ед.

Пример 3.3. В условиях примера 3.2. требуется составить план перевозок с минимальными затратами. При этом необходимо выполнить следующее дополнительное требование: спрос магазина МГ1 должен быть обязательно удовлетворен полностью.

Как и в примере 3.2, для приведения этой задачи к правильному балансу необходимо добавить фиктивного поставщика (склад СК5) с запасом товара в размере 15 тонн. Однако стоимость перевозки единицы товара от фиктивного поставщика в магазин МГ1 следует считать очень большим числом (например, 1000 ден.ед.). Стоимости перевозки единицы товара от фиктивного поставщика в другие магазины будем считать равными нулю. Расчетная таблица для этой задачи показана в табл. 3.18.

Получена задача с правильным балансом. Она решается точно так же, как обычная транспортная задача. Сначала по методу минимального элемента определяется допустимый план (табл. 3.19), затем по методу потенциалов – оптимальный план (табл. 3.20). Эти методы обеспечивают получение плана перевозок и минимальными затратами. Поэтому перевозки с фиктивного склада СК5 в магазин МГ1 не войдут в базис (т.е. примут нулевое значение), так как затраты на эти перевозки предполагаются очень большими.

Таблица 3.18

 

Таблица 3.19 Таблица 3.20

 

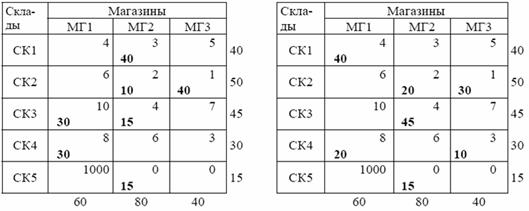
Для данной задачи получен следующий оптимальный план перевозок. Склад СК1 поставляет 40 тонн товара магазину МГ1; склад СК2 поставляет 20 тонн товара магазину МГ2 и 30 тонн – магазину МГ3; склад СК3 поставляет 45 тонн товара магазину МГ2; склад СК4 поставляет 20 тонн товара магазину МГ1 и 10 тонн – магазину МГ3. Магазину МГ2 будет поставлено на 15 тонн товара меньше, чем ему требуется (т.е. всего 65 тонн вместо 80 необходимых). Общие затраты на перевозки составят 600 ден.ед.

Пример 3.4. В условиях примера 3.2 требуется составить план перевозок с минимальными затратами. При этом необходимо выполнить следующее дополнительное требование: недопоставка товара распределяется равномерно между всеми магазинами. Это означает, что каждый из магазинов должен получить несколько меньше товара, чем ему требуется.

Для приведения такой задачи к правильному балансу предполагается, что спрос всех потребителей снизился. Для этого величины спроса умножаются на коэффициент , т.е. на отношение суммы величин спроса к сумме запасов. Вводить фиктивного поставщика в этом случае не требуется.

В рассматриваемом примере сумма величин спроса равна 180, сумма запасов – 165. Значит, величины спроса умножаются на коэффициент, равный 165/180=0,917.

Можно сказать, что таким образом спрос магазинов корректируется с учетом возможностей поставщиков (складов). Уменьшенная величина спроса для магазина МГ1 составит 60 ∙ 0,917 = 55,02 тонны, для магазина МГ2 – 80 ∙ 0,917 = 73,36 тонны, для МГ3 – 40 ∙ 0,917 = 36,68 тонны. Округлим эти величины до целых чисел (будем считать, что величины спроса магазинов должны выражаться целыми числами). Расчетная таблица для данной задачи приведена в табл. 5.21.

Полученная задача с правильным балансом решается обычным образом. Оптимальный план для рассматриваемой задачи приведен в табл. 3.22.

 

Таблица 3.21 Таблица 3.22

 

Таким образом, получен следующий оптимальный план перевозок. Склад СК1 поставляет 40 тонн товара магазину МГ1; склад СК2 поставляет 28 тонн товара магазину МГ2 и 22 тонны – магазину МГ3; склад СК3 поставляет 45 тонн товара магазину МГ2; склад СК4 поставляет 15 тонн товара магазину МГ1 и 15 тонн – магазину МГ3. Недопоставка товара магазину МГ1 составит 60-55=5 тонн, магазину МГ2 – 80-73=7 тонн, магазину МГ3 – 40-37=3 тонны. Общие затраты на перевозки составят 583 ден.ед.

 

3.2.2.5 Вырожденное решение

Для того чтобы иметь возможность решить систему уравнений (3.1) при поиске оптимального плана перевозок по методу потенциалов, необходимо, чтобы количество базисных переменных всегда было в точности равно M+N-1. Если некоторые из базисных переменных принимают нулевые значения, то решение называется вырожденным. Необходимо учитывать некоторые особенности поиска оптимального плана при появлении вырожденного решения. Такое решение возникает в следующих случаях:

· при поиске допустимого плана – в случае, если запас товара у поставщика оказывается в точности равен спросу потребителя;

· при поиске оптимального плана – в случае, если при выборе переменной для исключения из базиса оказывается несколько переменных, имеющих одинаковое минимальное значение.

Рассмотрим пример, в котором возникают оба случая вырожденного решения.

Пример 3.5. С двух карьеров (К1 и К2) поставляются стройматериалы на три стройки (С1, С2, С3). Возможности карьеров по поставке стройматериалов (тонны), потребности строек (тонны) и стоимост