Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k +1 вектора — линейно зависима.
Обозначается dim L = k. Пространство L называется k - мерным. Иногда обозначается L k.
Векторы i и j — линейно независимая система векторов линейного пространства геометрических радиусов-векторов плоскости R2.
Рассмотрим произвольную систему из трёх векторов x, y, z.
На рисунке показано, что вектор z линейно выражается через векторы x и y: z = α1· x + α2· y.
Итак, в пространстве R2 существует система из двух линейно независимых векторов (i, j), а любые три вектора образуют линейно зависимую систему. То есть размерность пространства R2 равна 2, dim R2 = 2.
Вопрос №13.
Пусть L -- n -мерное линейное пространство, и e1,…,enи e1’,…,en’ -- два базиса в этом пространстве. Первый из них назовем "старым", а второй -- "новым". Пусть S -- матрица перехода а от старого базиса к новому.
Предложение 19.1 Пусть A -- линейное преобразование пространства L, и Aи A’ -- матрицы этого преобразования в старом и новом базисе соответственно. ТогдаA’= 
AS
Доказательство. Пусть x -- произвольный вектор пространства L, y -- его образ, то есть y=A(x). Пусть α и β -- координатные столбцы векторов xи y в старом базисе, а x’, y’ -- в новом. Тогда в силу формулы β=Aα имеем α=Sα’, β=Sβ'. Подставим эти выражения в предыдущую формулу, получаем Sβ’=A(Sα’). Откуда β’=( AS)α’. С другой стороны, в силу формулы β=Aα в новом базисе β’=A’α’. Сравнивая это равенство с предыдущим, получаем A’= AS.
Определение Две квадратных матрицы P и Q одного порядка называются подобными, если существует такая невырожденная матрица S, что P= QS.
Следствие Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
Вопрос №14.
Вектор х называется собственным вектором матрицы А, если найдется такое число λ, что выполняется равенство: Ах = λх. Само число λ называется собственным числом матрицы А.
Для произвольного вектора х =х1е1 + х2е2 + х3е3 результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса: Ах =х`1е1 + х`2е2 + х`3е3, где координаты x`i можно найти по формулам:
х`1 = a11x1 + a12x2 + a13x3
x`2 = a21x1 + a22x2 + a23x3,
x`3 = a31x1 + a32x2 + a33x3.
Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.
Подставив в формулы (9.3) x`j = λxj, получим систему уравнений для определения координат собственного вектора:
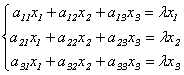
Отсюда
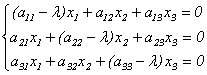
Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записавэтоусловие в виде:
получим уравнение для определения собственных чисел λ, называемое характеристическим уравнением. Кратко его можно представить тaк: | A- λE | = 0
Вопрос №15.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы через F1 и F2,расстояние между ними через 2с, а сумму расстояний от произвольной точки эллипса до фокусов — через 2а
По определению 2а > 2с, т.е. a > с.
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы F1 и F2 лежали на оси Ох, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы будут иметь следующие координаты:
и 
Пусть М(х;у) — произвольная точка эллипса. Тогда, согласно определению эллипса, 
, т. е. 
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение к более простому виду:
Так как a> с, то 
Положим 
Тогда последнее уравнение примет вид 
или 