в упругой пористой среде

4.12.1. Постановка задачи

 

При пуске скважин и эксплуатацию, при остановке их, при изменении темпа добычи жидкости из скважин в пласте возникают неустановившиеся процессы, которые проявляются в пере­распределении пластового давления (в падении или росте дав­ления вокруг скважины), в изменениях с течением времени дебитов, скоростей фильтрационных потоков и т. д.

Особенности этих неустановившихся процессов зависят от упругих свойств пластов и насыщающих их жидкостей. Хотя коэффициенты сжимаемости поды, нефти и пористой среды очень малы, упругость жидкостей и породы оказы­вает огромное влияние на поведение скважин и пластов в про­цессе их эксплуатации, так как объемы пласта и насыщающей его жидкости могут быть очень велики. Поэтому при подсчете запасов нефти (и газа), при проектировании разработки нефтя­ных и газовых месторождений, при эксплуатации, при исследо­вании скважин, при создании подземных хранилищ газа прихо­дится учитывать сжимаемость жидкости и пористой среды. Объем, насыщающей пласт жидкости при снижении пласто­вого давления увеличивается, а объем порового пространства уменьшается; это и определяет вытеснение жидкости из пласта в скважину (или газовую залежь).

Если в процессе разработки преобладающей формой энер­гии является энергия упругой деформации пласта и сжатой жидкости, то режим пласта называется упругим. При этом предполагается, что фильтрационный поток однофазный, т. е. пластовое давление выше давления насыщения.

В условиях упругого режима характерно то, что процесс перераспределения давления происходит медленно (длительно), а не мгновенно, как это было бы при абсолютной несжимае­мости пласта и насыщающей его жидкости.

В теории упругого режима большую роль играют два пара­метра:

Коэффициент упругоемкости пласта

(4.118)

где m — пористость; β_рж и β_рс - соответственно коэффициенты сжимаемости жидкости и пористой среды.

Коэффициент β_р^* численно равен изменению упругого запаса жидкости в единице объема пласта при изменении пластового давления на одну единицу. Иногда вместо коэффициента упругоемкости пласта используют приведенный модуль упругости

(4.119)

Коэффициент пьезопроводности пласта - характеризует темп перераспределения пластового давления в условиях упругого режима, впервые была введена В. Н. Щелкачевым.

(4.120)

4.12.2. Точные решения дифференциального уравнения

упругого режима

 

Дифференциальное уравнение упругого режима фильтрации можно записать

(4.121)

Интегрируя дифференциальное уравнение (4.121) при за­данных начальном и граничных условиях, определяют давле­ние в любой точке пласте в любой момент времени. Решение задачи перераспределения давления после пуска скважины с постоянным дебитом Q в бесконечном горизонталь-ком пласте сводится к интегрированию дифференциального уравнения (4.121), имеющего для плоскорадиальной фильтра­ции вид

(4.122)

с начальным и граничными условиями:

при t=0,

, (4.123)

при .

Точное решение этой задачи при r_c=0 дается формулой

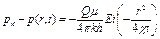(4.124)

(4.125)

Формула (4.124) является основной формулой упругого ре­жима пластов, широко применяющейся при исследовании про­цесса перераспределения пластового давления, вызванного пус­ком скважин с постоянными дебитами, остановкой скважин, изменениями темпов добычи и т. д. Формулу (4.124) также можно использовать в случае при­тока жидкости к скважине конечного радиуса и в начальной стадии изменения давления в пласте конечных размеров.

 

4.12.3. Метод последовательной смены стационарных состояний

В связи со сложностью точных решений были приложены различные приближенные методы решения задач неустановившейся фильтрации упругой жидкости. Одним из наиболее распространенных приближенных методов является метод последовательной смены стационарных состояний. Метод заключается в том, что в какой то момент времени зона пониженного давления (возмущенная зона) считается распространенной на определенное расстояние l=l(t) (приведенный радиус влияния) и предполагается так, как будто движение жидкости установившееся. В действительности же распределение давления в пласте не будет стационарным и зона пониженного давления захватит теоретически весь пласт. Закон изменения во времени приведенного радиуса влияния l(t) определяется из условия материального баланса. При неустановившемся притоке упругой жидкости к галерее , если отбор проводится при постоянной депрессии ; , если задан постоянный дебит

При плоскорадикальном притоке упругой жидкости к скважине можно считать с точностью до 10-15%, что (если ) как для случая постоянной депрессии, так и для постоянного отбора.

В методе А.М. Пирвердяна эпюра давления задается так, чтобы она не имела угловых точек. Например, при притоке к галерее распределение давления по пласту задается в виде параболы, касательная к которой в точке х=l(t) горизонтальна (рис. 4.23).

Рис. 4.23. Распределение давления в пласте

 

Если отбор жидкости не меняется с течением времени, т.е.

то

(4.126)

где

(4.127)

а приведенный радиус влияния, найденный из уравнения материального баланса, определяется по формуле

(4.128)

 

4.12.4. Суперпозиция в задачах упругого режима

Метод суперпозиции (наложения фильтрационных потоков) широко применяется и в задачах неустановившихся течений при упругом режиме.

Если в пласте действует группа скважин, то понижение давления в какой-либо точке пласта определяется сложением понижений давления, создаваемых в этой точке отдельными скважинами

(4.129)

где n – число скважин; - дебит j -той скважины, причем , если скважина эксплуатационная и , если скважина нагнетательная; - расстояние от j- той скважины до точки, в которой определяется понижение давления.

Если скважины начали работать в разное время, то (4.129) будет иметь вид

(4.130)

Пусть скважина продолжает работать с тем же дебитом, тогда к моменту t после остановки понижение давления в какой-либо точке пласта, вызванное пус­ком непрерывно работающей скважины, будет равно

(4.131)

Допустим в том же месте, где расположена эксплуатационная скважина, в момент остановки начала рабо­тать нагнетательная скважина с тем же дебитом. К моменту t повышение давления в какой-либо точке пласта, вызванное пуском нагнетательной скважины, определится по формуле

(4.132)

Результирующее понижение давления р запишется в виде

. (4.133)

Если аргументы функций малы, тогда

(4.134)

 

5. ОСНОВЫТЕОРИИ ЛОПАСТНЫХ НАСОСОВ

 

5.1. Основные рабочие параметры лопастных насосов

 

Гидравлическими машинами называются машины, которые сооб­щают протекающей через них жидкости механическую энергию (насос), либо получают от жидкости часть энергии и передают ее рабочему органу для полезного использования (гидравлический двигатель). Насосы являются одной из самых распространенных разновидностей машин. Их применяют для различных целей, начи­ная от водоснабжения населения и предприятий и кончая подачей топлива в двигателях ракет. Гидродвигатели имеют большое зна­чение в энергетике. В настоящее время в России около 20 % всей электроэнергии вырабатывается на гидроэлектростанциях. Для использования гидравлической энергий рек и преобразования ее в механическую энергию вращающегося вала генератора на ги­дроэлектростанциях применяют гидротурбины, являющиеся одной из разновидностей гидродвигателей. Мощность современных гид­ротурбин доходит до 650 тыс. кВт. Турбины используют и при буре­нии скважин.

Насосы и гидродвигатели применяют также в гидропередачах, назначением которых является передача механической энергии от двигателя к исполнительному рабочему органу, а также пре­образование вида и скорости движения последнего посредством жидкости. Гидропередача состоит из насоса и гидродвигателя. Насос, работающий от двигателя, сообщает жидкости энергию. Пройдя через насос, жидкость поступает в гидродвигатель, где передает механическую энергию исполнительному рабочему органу. Назначение гидропередач такое же, как и механических передач (муфты, коробки скоростей, редукторы и т. д.), однако по сравне­нию с последними они имеют следующие преимущества.

1. Большая плавность работы. Люфты, неизбежные в элементах механической передачи, а также неточность ее изготовления приво­дят к вибрациям. Включение и выключение механической передачи или изменение ее передаточного числа сопровождается толчками.

2. Возможность получения бесступенчатого изменения передаточ­ного числа. В механических передачах изменение передаточного числа обычно производится ступенями. Механические передачи, допускающие бесступенчатое изменение передаточного числа (на­пример, фрикционные), недостаточно надежны и могут применяться только при малой мощности.

3. Возможность получения меньшей зависимости момента на веду­щем валу от нагрузки, приложенной к исполнительному органу. Это упрощает обслуживание машин и предохраняет двигатель и транс­миссию от перегрузки.

4. Возможность передачи больших мощностей.

5. Малые габаритные размеры и масса.

6. Высокая надежность.

Эти преимущества привели к большому распространению гидро­передач, несмотря на их несколько меньший, чем у механических передач КПД.

В современной технике" применяется большое количество разно­видностей гидромашин. Наибольшее распространение получили объемные и лопастные насосы и гидродвигатели. Объемные гидромашины (поршневые, шесте­ренные, аксиально-поршне­вые и т. д.) работают за счет изменения объема ра­бочих камер, периодически соединяющихся с входным и выходным патрубками. Ра­бочим органом лопастной ма­шины является вращающее­ся рабочее колесо, снабжен­ное лопастями. Энергия от рабочего колеса жидкости (лопастный насос) или от жидкости рабочему колесу (лопастный двигатель) передается путем динамического взаимодействия лопастей колеса с обтекающей их жидкостью. К лопастным насосам отно­сятся центробежные и осевые.

На рис. 5.1 изображена простейшая схема центробежного насоса. Проточная часть насоса состоит из трех основных элементов — под­вода 1, рабочего колеса 2 иотвода 3. По подводу жидкость подается в рабочее колесо из подводящего трубопровода. Назначением рабо­чего колеса является передача жидкости энергии от двигателя. Рабочее колесо центробежного насоса состоит из ведущего а и ведо­мого (обода) б дисков, между которыми находятся лопатки в, изогнутые, как правило, в сторону, противоположную направле­нию вращения колеса. Ведущим диском рабочее колесо крепится на валу. Жидкость движется через колесо из центральной его части к периферии. По отводу жидкость отводится от рабочего колеса к напорному патрубку или, в многоступенчатых насосах, к сле­дующему колесу.

Рис. 5.1. Схема центробежного насоса консольного типа.

1 – подвод; 2 – рабочее колесо; 3 – отвод; 4 – диффузор; 5 – язык.

 

К наиболее распространенным лопастным гидродвигателям отно­сятся радиально-осевые и осевые гидротурбины. Радиально-осевая гидротурбина принципиально не отличается по конструкции от цен­тробежного насоса. Направление движения жидкости в ней и направление вращения колеса противоположны движению в центро­бежном насосе. Радиально-осевая турбина и центробежный насос являются обратимыми машинами и могут работать как в турбинном, так и в насосном режимах.

Рассмотрим подробнее механизм передачи энергии в лопастной гидромашине. При обтекании потоком крылового профиля (напри­мер, крыла самолета) на его верхней и нижней поверхностях обра­зуется перепад давления и, следовательно, возникает сила Р (рис. 5.2), которая называется подъемной силой. Аналогично этому возникает подъемная сила на лопатках рабочего колеса лопастной гидромашины при движении их в жидкости.

 

 

Рис. 5.2. Сила, действующая на крыловой профиль

 

У лопастного насоса направление момента подъемных сил противоположно направлению вращения рабочего колеса. Преодолевая этот момент при вращении, колесо совершает работу. Для этого к колесу от двигателя подводится энергия, которая, согласно закону сохранения энергии, передается жидкости и увеличивает ее удельную энергию. В дальнейшем удель­ная энергия жидкости частично превращается в тепло из-за трения между слоями жидкости в насосе и, следовательно, теряется, частично остается в форме механической удельной энергии, составляя полезный напор насоса. Насос конструируют так, чтобы потери энергии были, возможно, малыми.

У лопастного двигателя (гидротурбины) направление момента подъемных сил совпадает с направлением вращения колеса. Воздей­ствуя на лопатки, жидкость вращает рабочее колесо, передавая ему энергию.

Лопастные насосы бывают одноступенчатыми и многоступенча­тыми. Одноступенчатые насосы имеют одно рабочее колесо, много­ступенчатые - несколько последовательно соединенных рабочих ко­лес, закрепленных на одном валу. На рис. 5.1 изображен односту­пенчатый насос консольного типа. Рабочее колесо у этих насосов закреплено па конце (консоли) вала. Вал не проходит через область всасывания, что позволяет применить простейшую форму подвода в виде прямоосного конфузора.

На рис. 5.3 изображен одноступенчатый насос двустороннего входа. Он имеет раздваивающийся спиральный подвод (см. рис. 5.47). Жидкость входит в рабочее колесо с двух сторон двумя потоками. В рабочем колесе эти потоки соединяются и выходят в общий отвод.

Рис. 5.3. Одноступенчатый насос двустороннего типа.

 

Одноступенчатые насосы сообщают жидкости ограниченный на­пор. Для повышения напора применяют многоступенчатые на­сосы, в которых жидкость проходит последовательно через несколько,рабочих колес, закрепленных на одном валу (рис. 5.4). При этом пропорционально числу колес увеличивается напор насоса.

Рис. 5.4. Схема многоступенчатого секционного центробежного насоса:

1 – рабочее колесо; 2 – направляющий аппарат; 3 – гидравлическая пята.

Осевые насосы будут рассмотрены в п. 5.8.

 

5.1.1. Подача, напор и мощность насоса

 

Работа насоса характеризуется его подачей, напором, потреб­ляемой мощностью, КПД и частотой вращения. Подачей насоса называется расход жидкости через напорный (выходной) патру­бок. Так же как и расход, подача может быть объемной (Q) и мас­совой (Q_m). Напор Н представляет собой разность энергий единицы веса жидкости в сечении потока после насоса z_н+p_н/(ρg)+υ_н²/(2g) и перед ним z_в+p_в/(ρg)+υ_в²/(2g):

Н = z_н - z_В + (p_н – p_в)/(ρg)+(υ_н² – υ_в²)/(2g) (5.1)

и выражается в метрах.

Мощностью насоса (мощностью, потребляемой насосом) назы­вается энергия, подводимая к нему от двигателя за единицу вре­мени. Мощность можно определить из следующих соображений. Каждая единица веса жидкости, прошедшая через насос, приобре­тает энергию в количестве Н, за единицу времени через насос про­текает жидкость весом Qρg. Следовательно, энергия, приобретен­ная за единицу времени жидкостью, прошедшей через насос, или полезная мощность насоса

N_{п =} QρgH. (5,2)

Мощность насоса N больше полезной мощности N_п на величину потерь в насосе. Эти потери оцениваются КПД насоса ŋ,который равен отношению полезной мощности насоса к потребляемой:

ŋ = N_п / N. (5.3)

Отсюда мощность, потребляемая насосом,

N=QρgH/ŋ. (5.4)

По этой мощности подбирается двигатель. Найденные по уравне­ниям (5.2) и (5.4) мощности выражаются в единицах СИ в ваттах, в технической системе единиц – в кг ∙ м/с.

 

5.1.2. Баланс энергии в лопастном насосе

 

На рис. 5.5 изображен баланс энергии в лопастном насосе. К насосу подводится мощность N. Часть этой мощности теряется (превращается в тепло). Потери мощ­ности в насосе делят на механиче­ские, объемные и гидравлические.

Рис. 5.5. Баланс энергии в лопастном насосе

 

Механические потери. Механи­ческими являются потери на тре­ние в подшипниках, в уплотне­ниях вала и на трение наружной поверхности рабочих колес о жид­кость (дисковое трение).

Мощность, остающаяся за вы­четом механических потерь, передается рабочим колесом жидкости. Ее принято называть гидравлической.Энергия, переданная рабочим колесом единице веса прохо­дящей через него жидкости, называется теоретическим напором Н_т. Он больше напора Н насоса на величину гидравлических потерь h_п при течении жидкости в рабочих органах насоса:

H_т= Н + h_п. (5.5)

Через рабочее колесо протекает в секунду жидкость объемом Q_к или весом Q_кρgH_т. Следовательно, гидравлическая мощность насоса, т. е. мощность, сообщаемая жидкости в колесе,

N_Г=Q_кρgH_т (5.6)

Величина механических потерь оценивается механическим КПД, который равен отношению оставшейся после преодоления механи­ческих сопротивлений гидравлической мощности N_Г к мощности N, потребляемой насосом

ŋ _мех = N_Г/N. (5.7)

Объемные потери. Рассмотрим объемные потери в одноступенча­том насосе. Жидкость, выходящая из рабочего колеса в количестве Q_К, в основном поступает в отвод (Q) и, следовательно, в напорный патрубок насоса, и частично возвращается в подвод через зазор в уплотнении 1 между рабочим колесом и корпусом насоса (утечка q_к, рис. 5.6). Энергия жидкости, возвращающейся в подвод, теряется. Эти потери называются объемными. Утечки обусловлены тем, что давление на выходе из рабочего колеса больше, чем в подводе.

Утечки тем значительнее, чем больше зазор в уплотнении 1 между рабочим колесом и корпусом насоса. Для того чтобы уменьшить утечки, следует уменьшить этот зазор до минимума, допускаемого технологией изготовления и деформацией вала и корпуса насоса при их нагрузке во время работы.

 

Рис. 5.6. Утечки в уплотнении рабочего колеса

 

Кроме рассмотренных утечек жидкости имеют место утечки через уплотнения вала. Они обычно малы и при рассмотрении баланса мощности ими можно пренебречь.

Объемные потери оценивают объемным КПД, равным отношению мощности N', оставшейся за вычетом мощности, затрачиваемой на объемные потери, к гидравлической мощности N_Г (см. рис. 5.5):

ŋ ₀ = N'/N_Г = (N_Г – N_О)/N_Г, (5.8)

где N_О — мощность, затрачиваемая на объемные потери.

Каждая единица веса жидкости, протекающей через уплотнение рабочего колеса, уносит энергию Н _T. Следовательно, мощность, затрачиваемая на объемные потери

N_O = q_kgH_т.

Так как расход через колесо Q_к = Q + q_к (см. рис. 5.6),

N' = N_Г – N_О = Q_кρqH_Т - q_kρgH_т (5.9)

Подставив выражения (5.9) и (5.6) в уравнение (5.8), получим

ŋ _O = Q/Q_k = Q/(Q + q_k) (5.10)

В многоступенчатых насосах секционного типа (см.рис.5.4.) также имеются утечки жидкости через зазоры между валом и перегородками — диафрагмами, разделяющими ступени, и через гидравлическую пяту 3. Потери энергии, обусловленные утечками через уплотнения диафрагм, относятся к ги­дравлическим и механическим потерям, а через гидравлическую пяту — к объемным. Для многоступенчатых секционных насосов объемный КПД определяется также по уравнению (5.10), однако при этом под q_k следует понимать не утечку через уплотне­ние рабочего колеса одной ступени, а сум­му этой утечки и утечки q_п в гидравличес­кой пяте.

Гидравлические потери. Третьим видом потерь энергии в насосе являются потери на преодоление гидравлического сопротивления подвода, рабочего колеса и отвода, или гидравлические потери. Они оцениваются гидравлическим КПД ŋ _г, который равен отношению полезной мощ­ности насоса N_п к мощности N' (см. рис. 5.5). Согласно уравнениям (5.2), (5.5).

ŋ_г = N_П/N' = H/H_т = H/(H+h_п) (5.11)

Как было указано в п. 5.2, КПД насоса

ŋ = N_П/ N

Умножив и разделив правую часть уравнения на N_Г N', получим

ŋ = N_П/N' ∙ N'/N_Г ∙N_Г/N = ŋ _Г ŋ _О ŋ _мех,(5.12)

т. е. КПД насоса равен произведению гидравлического, объемного и механического КПД.

 

5.1.3. Основное уравнение лопастных насосов

 

Основное уравнение лопастных насосов можно вывести на осно­вании уравнения (1.187) моментов количества движения

М = Q_т(υ_u²R₂ – υ_u1R₁),

примененного для жидкости, находящейся в рабочем колесе насоса, которое представляет собой систему каналов. Рассматриваемый объем жидкости ограничен изнутри и по периферии поверхностями вращения, образующими которых являются входные и выходные кромки лопаток. Момент сил давления на эти границы равен нулю, так как нормали к поверхностям вращения проходят через ось ко­леса. Силы трения на указанных границах пренебрежимо малы. Поэтому момент М, действующий па жидкость в колесе, обусловлен только воздействием на нее стенок каналов колеса (лопаток и внутрен­них поверхностей ведущего и ведомого дисков). Под величиной Q_т следует понимать массовый расход Q_тк =Q_kρ жидкости через колесо.

Умножим последнее уравнение на угловую скорость ω рабочего колеса. Произведение М _ωесть секундная работа, которую совер­шает рабочее колесо, воздействуя на находящуюся в нем жидкость. Эта работа равна энергии, передаваемой рабочим колесом жидкости за единицу времени, или гидравлической мощности N_г. Отсюда

N_г= Q_mkω(υ_u²R₂ – υ_u¹R₁)_.

Согласно уравнению (5.6) с учетом того, что Q_kρ = Q_mk,

N_г= Q_mkgH_т.

Следовательно,

Q_mkgH_т= Q_mkω(υ_u²R₂ – υ_u¹R₁)

H_т= Н/ŋ_г= (ω/g)(υ_u²R₂ – υ_u¹R₁) (5.13)

Полученное основное уравнение лопастных насосов было впер­вые выведено Эйлером. Оно связывает напор насоса со скоростями движения жидкости, которые зависят от подачи, и частоты враще­ния насоса, а также от геометрии рабочего колеса и подвода. Поток на входе в колесо создается предшествующим колесу устройством — подводом. Следовательно момент скорости υ_u¹R₁ на входе в колесо определяется конструкцией подвода и практически не зависит от конструкции колеса. Поток на выходе из колеса создается самим коле­сом, поэтому момент скорости υ_u²R₂ определяется конструкцией колеса, особенно геометрией его выходных элементов (наружным диаметром, шириной лопаток, углом установки их на выходе). Основное уравнение дает возможность по заданным напору, частоте вращения и подаче насоса рассчитать выходные элементы рабочего колеса.

Подводы многих конструкций, например прямоосный конфузор, не закручивают поток и момент скорости υ_u¹R₁= 0. В этом случае теоретический напор

H_т= (ω/g)υ_u²R₂ (5.14)

 

5.1.4. Движение жидкости в рабочем колесе центробежного насоса

 

В рабочем колесе насоса частицы жидкости движутся относи­тельно рабочего колеса и, кроме того, они вместе с ним совершают переносное движение. Сумма относительного и переносного движений дает абсолютное движение жидкости, т. е. движение ее относительно неподвижного корпуса насоса. Скорость абсолютного движения υ (абсолютная скорость) равна геометрической сумме скорости ω жидкости относительно рабочего колеса (относительной скорости) и окружной скорости и рабочего колеса (переносной скорости):

υ¯=ω¯+u¯. (5.15)

Для упрощения рассуждений допускаем, что поток в рабочем колесе осесимметричный. При этом траектории всех частиц жидкости в относительном движении одинаковы. Примем, что они совпадают с кривой очертания лопатки АВ (рис. 5.7). Относительные скорости частиц жидкости, лежащих на одной окружности, одинаковы и на­правлены по касательной к поверхности лопатки в рассматриваемой точке. Указанные допущения часто называют схемой бесконечного числа лопаток. В действительности поток жидкости в рабочем колесе не является осесимметричным. Давление на лицевой стороне лопатки (передняя сторона лопатки по отношению к направлению ее движения) больше, чем на ее тыльной стороне. Согласно уравне­нию Бернулли, чем больше давление, тем меньше скорость. Поэтому относительная скорость частиц, движущихся вдоль лицевой сто­роны лопатки, меньше относительной скорости частиц, движущихся вдоль ее тыльной стороны. Относительные траектории частиц, непо­средственно примыкающих к лопатке, совпадают по форме с лопат­кой. Траектории же остальных частиц отличаются от нее.

 

 

 

Рис. 5.7. Схема для рассмотрения движения жидкости в рабочем колесе

 

Из уравнения (5.15) следует, что скорости υ, ω и и образуют треугольник скоростей. На рис. 5.7 изображено сложение скоро­стей для произвольной точки К внутри колеса. Согласно схеме бесконечного числа лопаток, относительная скорость ω направлена по касательной к лопатке. Окружная скорость и направлена по каса­тельной к окружности, на которой расположена рассматриваемая точка, в сторону вращения рабочего колеса.

Разложим абсолютную скорость υна две взаимно перпендику­лярные составляющие: υ _и - окружную составляющую абсолютной скорости и υ_м -меридиональную скорость — проекцию абсолютной скорости на плоскость, проходящую через ось колеса и рассматри­ваемую точку. Эта плоскость называется меридиональной.

Введем следующие обозначения:

α - угол между абсолютнойυ и переносной и скоростями жид­кости;

β - угол между относительной скоростью ωи отрицательным направлением переносной скорости и жидкости;

β_л - угол между касательной к лопатке и отрицательным на­правлением переносной скорости и жидкости.

Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 для обозначения тех же величин на выходе из него.

Построим треугольник скоростей для точки G входной кромки ЕF рабочего колеса (см. рис. 5.7). Меридиональную скорость υ_м1 опре­делим из уравнения расхода. Принимая распределение меридиональ­ных скоростей по ширине рабочего колеса равномерным, получим

υ_м1= Q_k/S₁= Q/(ŋ_oS₁) (5.16)

где Q_k – расход жидкости, протекающей через колесо; S₁ — площадь нор­мального сечения меридионального потока.

Меридиональным называют воображаемый поток, движущийся через рабочее колесо со скоростями, равными меридиональным. Иными словами, меридиональный поток есть поток, протекающий без окружной скорости через полость вращения, образованную ведомым и ведущим дисками рабочего колеса. Нормальное сечение меридионального потока имеет форму поверхности вращения. Она образована вращением вокруг оси колеса линии СD, пересекающей под прямыми углами линии тока меридионального потока, и про­ходящей через точку G. Согласно теореме Гюльдена, площадь S₀ этой поверхности вращения равна произведению длины b₁ образую­щей СD на длину окружности, описываемой центром тяжести линии СD при ее вращении вокруг оси насоса:

S_o = 2πR_ц1b₁, (5.17)

где R_Ц1 — радиус, на котором расположен центр тяжести линии СD.

Часть поверхности вращения занята телом лопаток, поэтому искомая площадь нормального сечения меридионального потока S₁=ψ₁S_o, где ψ₁- коэффициент стеснения на входе в рабо­чее колесо.

Величина ψ₁ определяется из следующих соображений. Площадь

S1= 2πR_ц1b₁-σ₁b₁z,

где σ₁ - толщина лопатки на входе, измеренная в окружном направлении (рис. 5.8, стр. 220); z - число лопа­ток.

Приближенно из треуголь­ника АВС

σ₁~S₁/sin β_1л,

где S₁ – толщина лопатки на входе, измеренная по нормали к ее поверхности.

Отсюда

ψ₁= S₁/S_o= (2πR_ц1b₁-zσ₁)/(2πR_ц1) (5.18)

Рис. 5.8. Входной участок лопатки рабочего колеса

 

У наиболее распространенных насосов величина ψ₁ колеблется от 0,75 (малые колеса) до 0,88 (большие колеса).

Окончательно получим

υ_м1= Q/ (2πR_ц1b₁ψ₁ŋ_o) (5.19)

В п. 5.4 было отмечено, что момент скорости υ_u1R₁ и, следова­тельно окружная составляющая υ_u1 абсолютной скорости на входе определяются конструкцией подвода. Многие разновидности под­вода не закручивают поток, при этом υ_u1 = 0. Окружная составляю­щая абсолютной скорости на входе не равна нулю для спирального подвода и часто для обратных каналов направляющего аппарата, служащих подводом промежуточных сту­пеней секционных насосов.

Окружная скорость рабочего колеса

u₁₌ ωR₁, (5.20)

где ω – угловая скорость рабочего колеса; R ₁-радиус, на котором распо­ложена точка G входной кромки колеса (см. рис. 5.7).

Зная величины υ_м1, υ_и1 и и₁, можно построить треугольник скоростей на входе (рис. 5.9) и, следовательно, определить относи­тельную скорость ω₁ и углы α₁ и β₁.

Направление входного элемента лопатки следует выбирать близ­ким к направлению относительной скорости ω₁.В противном слу­чае получается отрыв потока от лопатки с образованием вихревой зоны (см. рис. 5.12, б), сильно увеличивающей потери па входе в рабочее колесо. Опыт показывает, что как КПД, так и высота, на которую насос способен засосать жидкость (высота всасывания), увеличиваются, если входной элемент лопатки рабочего колеса установить по отношению к окружности не под утлом β₁, получаю­щимся из треугольника скоростей входа, построенного для рас­четной подачи насоса, а под углом β_1Л, большим угла β₁ на 3—8°. При таком небольшом отклонении входного элемента лопатки от на­правления относительной скорости отрыва потока от лопатки не полу­чается. Назовем угол менаду направлением относительной скорости и направлением входного элемента лопатки углом атаки.

Начальный участок лопатки утоняют по направлению к входной кромке примерно в 2 раза (см. рис. 5.8) на длине, равной 1/3—1/4 длины лопатки, причем входную кромку лопатки скругляют. Благодаря этому улучшаются ус­ловия обтекания входной кром­ки и уменьшаются гидравличе­ские потери на входе жидкости на лопатки рабочего колеса. Кроме того, при этом увеличи­вается высота всасывания на­соса.

При построении треугольни­ка скоростей входа было учтено стеснение потока лопатками. Следовательно, треугольник скоростей построен для точки, расположенной непосредственно за входом на лопатки рабочего колеса. Для некоторых расчетов необходимо знать относительную и абсолютную скорости потока непосредственно перед входом на лопатки, т. е. потока, не возмущенного лопатками. Введем индекс О для обозначения скоростей этого потока. Учитывая уравнение (5.17), получим меридиональную скорость

υ_м0 = Q/ (S₀ŋ₀)= Q/2πR_ц1b₁ŋ₀ (5.21)

Стеснение потока лопатками не может сказаться на величине окружной составляющей абсолютной скорости. Следовательно,

υ_u0= υ_{u1 .}

Треугольник скоростей перед входом в рабочее колесо изображен на рис. 5.9 штриховой линией. Пунктирная линия показывает направление входного элемента лопатки)

 

Рис. 5.9. Треугольник скоростей на входе в рабочее колесо (штрих-

 

Жидкость выходит из рабочего колеса через цилиндрическую поверхность площадью

S₂= 2πR₂b₂ψ₂,

где R₂ - наружный радиус рабочего колеса (см. риc. 5.7); b₂ - ширина канала рабочего колеса на выходе; ψ₂ -коэффициент стеснения на выходе из рабочего колеса.

Коэффициент ψ₂ определяется но уравнению

ψ₂= (2πR₂-zσ₂)/(2πR₂), ( 5. 22)

где σ₂ – толщина лопатки на выходе, измеренная в окружном направлении:

σ₂= S₂/sin β_2л (5.23)

У наиболее распространенных насосов величина ψ₂ колеблется от 0,9 (малые насосы) до 0,95 (большие насосы).

Меридиональная скорость на выходе

υ_м2=Q/(2πR₂b₂ ψ₂ŋ₀) (5.24)

Окружная скорость рабочего колеса на выходе

υ_м2= ωR₂ (5.25)

Окружная составляющая скорости жидкости на выходе из рабо­чего колеса υ_u2 определяется из уравнения Эйлера (5.13) но извест­ному напору насоса. Зная величины υ_м2, u₂ и υ_м2 можно построить треугольник скоростей на выходе из колеса (рис. 5.10, треугольник АDС)и определить из него величину и направление относительной скорости ω₂. Опыт пока­зывает, что направление относительной скорости ω₂ не совпадает с направле­нием выходного элемента лопатки, что не соответcт­вует схеме бесконечного числа лопаток. Причина этого отклонения относи­тельного потока жидкости от выходного элемента лопаток в инерции жидкости. Рабочее колесо закручивает жидкость, увеличивая момент абсолютной скорости υ_uR. Инерция препятствует этому изменению момента скорости. При б