Теорема 6.1 (критерий Эйзенштейна). Пусть f = a 0 + a 1 x + … + anxn – многочлен с целыми коэффициентами. Если существует такое простое число p, что a 0, a 1, …, an -1 делятся на p, an не делится на p, a 0 не делится на p 2, то f не приводим над полем рациональных чисел.
Упражнение 6.1. Докажите неприводимость над Q многочленов:
а) f = 2 х 5 + 3 х 4 – 9 х 3 – 6 х + 3; б) f = 5 х 4 + 6 х 3 – 18 х 2 – 12 х + 54.
Теорема 6.2. Пусть 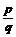 – несократимая дробь, являющаяся корнем многочлена f = a 0 + a 1 x + … + anxn с целыми коэффициентами. Тогда
– несократимая дробь, являющаяся корнем многочлена f = a 0 + a 1 x + … + anxn с целыми коэффициентами. Тогда
1) a 0 M p, an M q;
2) f (1) M p – q, f (–1) M p + q.
Эта теорема позволяет решить задачу отыскания рациональных корней многочлена с целыми коэффициентами. Для этого определяем все делители свободного члена и старшего коэффициента и строим из них всевозможные несократимые дроби. Все рациональные корни содержатся среди этих дробей. Для их определения можно использовать схему Горнера. Чтобы избежать в ней лишних вычислений, используем утверждение 2) теоремы 6.2.
Пример 6.1. Найти рациональные корни многочлена
f = 2 х 4 + 7 х 3 + 3 х 2 – 15 х – 18.
Решение. Выписываем все дроби, числители которых p – делители 18, а знаменатели q – делители 2:
1, –1, 2, –2, 3, –3, 6, –6, 9, –9, 18, –18, 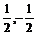 ,
, 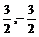 ,
, 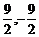 .
.
Производим их проверку по схеме Горнера:
| –15 | –18 | Комментарий | ||||
| –3 | –21 | f (1) = –21 M p – q | ||||
| –1 | –2 | –13 | –3 | f (–1) = –3 M p + q | ||
| –2 | –3 | –9 | х 1= –2 | |||
| 1/2 | –1 | –19/2 | ||||
| –1/2 | –4 | –7 | ||||
| 3/2 | х 2= 3/2 | |||||
Найдя корень х 1= –2 и разделив многочлен на х + 2, получили многочлен с новым свободным членом –9 (его коэффициенты подчеркнуты). Числители остальных корней должны быть делителями этого числа, и из списка можно исключить дроби, не удовлетворяющие этому условию. Остальные целые значения исключены, так как не удовлетворяют условию f (1) M p – q или f (–1) M p + q. Например, для 3 имеем p = 3, q = 1, и не выполняется условие f (1) = –21 M p – q (как и второе условие).
Аналогично найдя корень х 2= 3/2, получили многочлен с новым свободным членом 3 и старшим коэффициентом 1 (когда корень дробный, следует произвести сокращение коэффициентов получившегося многочлена). Ни одно оставшееся число из списка больше не может быть его корнем, и список рациональных корней исчерпан.
Найденные корни следует проверять на кратность.
Если в процессе решения пришли к многочлену второй степени, а список дробей еще не исчерпан, то оставшиеся корни можно найти по обычным формулам как корни квадратного трехчлена.
Упражнение 6.2. Найдите рациональные корни многочлена
а) х 3 – 6 х 2 + 15 х – 14;
б) х 5 – 7 х 3 – 12 х 2 + 6 х + 36;
в) 2 х 4 – 11 х 3 + 23 х 2 – 24 х + 12;
г) 4 х 4 – 7 х 2 – 5 х – 1.
АЛГЕБРАИЧЕСКИЕ ЧИСЛА
В этом разделе все поля являются подполями поля комплексных чисел.
Число a называется алгебраическим над полем F, если a есть корень некоторого многочлена из F[ x ].
Число a называется алгебраическим, если a алгебраично над полем рациональных чисел. Это равносильно тому, что a есть корень многочлена с целыми коэффициентами. Число a, не являющееся алгебраическим, называется трансцендентным.
В школьном курсе алгебры рассматривается задача освобождения от квадратичной иррациональности в знаменателе дроби. Она решается с помощью домножения знаменателя на сопряженное выражение. Аналогично решается общая задача освобождения от иррациональности в знаменателе дроби.
Пример 7.1. Освободиться от иррациональности в знаменателе дроби 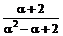 , где a3 – 3a + 3 = 0.
, где a3 – 3a + 3 = 0.
Решение. Число a есть корень многочлена j (х) = х 3 – 3 х + 3. В знаменателе дроби стоит значение f (a), где f (x) = x 2 – x + 2. Найдем НОД(j, f) и его линейное представление, как в примере 2.1. Получим
НОД(j, f) = 35 = (4 x + 3) j – (4 x 2 + 7 x – 13) f.
(нет необходимости делать НОД(j, f) = 1). Подставив значение х = a и воспользовавшись тем, что j (a) = 0, получим 35 = –(4a2 + 7a – 13) f (a). Значит, чтобы освободиться от иррациональности в знаменателе, достаточно умножить его на 4a2 + 7a – 13. На это же выражение умножаем числитель и получаем
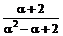 =
= 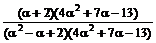 =
= 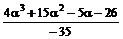 .
.
В числителе степень a следует понизить, сделав ее меньше, чем у j. Для этого разделим с остатком h (x) = 4 x 3 + 15 x 2 – 5 x – 26 на j (х). Получим
h (x) = 4 j (х) + 15 х 2 + 7 х – 38,
откуда h (a) = 15a2 + 7a – 38. Окончательно получаем
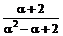 =
= 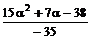 .
.
Упражнение 7.2. Избавьтесь от иррациональности в знаменателе дроби:
а)  , где a3 – 2a2 + 2 = 0;
, где a3 – 2a2 + 2 = 0;
б)  , где a3 + 4a + 2 = 0;
, где a3 + 4a + 2 = 0;
в) 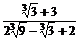 .
.