В процессе управления производством перед руководителем зачастую возникают проблемы в выборе решения. Ситуация разрешается сравнительно легко, когда имеется формальная модель, адекватно описывающая объект управления. Сложнее принимать управленческие решения, если необходимо учитывать множество различных факторов. Однако априори можно утверждать, что специалисты в конкретной области (эксперты) имеют вполне сложившиеся представления о влиянии тех или иных факторов. В этом случае используют результаты коллективного обсуждения проблемы и в качестве инструмента применяют метод экспертных оценок.
Предположим, что рассматривается некоторый процесс, который характеризуется множеством параметров (факторов) Xj, где j =1, 2… m. Это множество представляет собой избыточную совокупность, то есть количество параметров больше, чем необходимо для управления процессом. Необходимо из m параметров отобрать k наиболее информативных, причем k < m. Другими словами, для дальнейшего рассмотрения оставляют только часть наиболее важных параметров. К выделенной совокупности контролируемых параметров Xj, где j =1, 2… k, предъявляют следующие общие требования:
- она должна обладать достаточной информативностью, то есть добавление какого-либо параметра не должно приводить к значительному изменению критериев;
- совокупность выбранных параметров должна содержать возможно меньшее их количество с целью минимизации экономических затрат и технической трудоемкости;
- выделенная совокупность может состоять как из количественных, так и качественных параметров, причем значимость качественных параметров должна поддаваться количественной обработке (ранжировке), которая осуществляется с помощью экспертных оценок.
Количество экспертов (n) должно зависеть от вероятности P выбора правильного решения и допустимого разброса Δ мнений экспертов. Теория вероятностей и математическая статистика дают численные значения этих нормативных данных, часть которых приведена в таблице 5а.1.
Таблица 5а.1 – Наименьшая допустимая численность экспертов
| Δ, % P, % | |||
Эксперты каждому из полного перечня факторов присваивает ранг Rij,
где i — порядковый номер эксперта, n — количество экспертов;
j — порядковый номер фактора, m — количество факторов.
На первое место (Rij =1) ставится фактор с наибольшей значимостью, а наибольший ранг (Rij = m) присваивается наименее значимому фактору. Сумма рангов, назначенных всеми экспертами j -му фактору, определяется по формуле:
 .
.
Результаты ранжирования факторов экспертами сводятся в таблицу 5а.2. Она содержит совокупность рангов Rij и представляет собой матрицу | Rij |, которая дополнена совокупностью суммарных рангов Sj, которые представляют собой вектор-строку | Sj |.
Таблица 5а.2 – Ранжирование факторов экспертами
 Фактор
Эксперт Фактор
Эксперт
| … | m | ||
| R11 | R12 | … | R1m | |
| R21 | R22 | … | R2m | |
| … | … | … | … | … |
| n | Rn1 | Rn2 | … | Rnm |
| Sj | S1 | S2 | … | Sm |
Фактор с наименьшим суммарным рангом является наиболее значимым. На практике значимыми считаются те факторы, для которых выполняется условие:
Sj < Sср,
где Sср — средний суммарный ранг, рассчитываемый по формуле:
 .
.
Степень согласованности мнений экспертов можно оценить по величине коэффициента конкордации. Он представляет собой отношение дисперсии суммарных рангов исполнителей к максимальной дисперсии суммарных рангов, то есть:
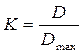 .
.
Дисперсия какой-либо величины есть характеристика ее рассеивания или разбросанности около среднего значения. Дисперсия D суммарных рангов рассчитывается следующим образом:
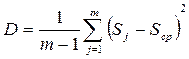 ,
,
Максимальная дисперсия Dmax суммарных рангов соответствует случаю, когда мнения всех экспертов совпадают. Ее можно рассчитать по формуле:
 .
.
В итоге получаем выражение для расчета коэффициента конкордации:
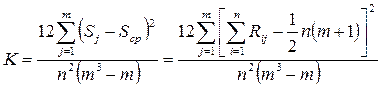 .
.
Из определения коэффициента конкордации следует, что он может принимать значения из интервала от 0 до 1. Чем ближе коэффициент конкордации к единице, тем более согласованными являются мнения экспертов. При полной согласованности мнений экспертов K = 1, то есть ранги, присвоенные факторам, у всех экспертов совпадают. Если коэффициент конкордации приближается к нулю, то это соответствует увеличению разброса мнений экспертов. Если мнения экспертов совершенно не коррелированны, то К = 0. На практике мнения экспертов считаются достаточно согласованными, если коэффициент конкордации удовлетворяет условию:
К ³ 0,4.
Если окажется, что К < 0,4, то эксперты предложили взаимно компенсирующие варианты. Это возможно в том случае, когда оцениваемые факторы близки друг к другу, не имеет смысла давать им количественные характеристики, либо эксперты оказались некомпетентными и не смогли прийти к единому мнению в ранжировании факторов.
Практическое задание
1. Изучите особенности применения метода экспертных оценок и методику обработки результатов.
2. Сформулируйте задачу, решаемую с применением метода экспертных оценок (например, задача может быть посвящена определению главных причин, приводящих к выходу из строя техники во время полевых работ).
3. Составьте перечень факторов (факторами могут являться различные причины выхода из строя техники во время полевых работ).
4. Сформируйте группу экспертов (в качестве экспертов выступают слушатели учебной группы).
5. Проведите оценку факторов и заполните матрицу рангов (таблица 5а.2).
6. Подсчитайте суммарные ранги для всех факторов. Выделите наиболее значимые факторы и проанализируйте полученный результат.
7. Рассчитайте коэффициент конкордации и сделайте вывод о степени согласованности мнений экспертов.
8. Подведите итоги, отметьте достоинства и недостатки метода экспертных оценок, наметьте круг решаемых с его помощью задач.