1 Перевести А и В (таблица 2.5) из десятичной системы в 8-разрядные прямой, обратный и дополнительный коды.
2 Перевести числа С и D (таблица 2.5) из десятичной системы двоично-десятичный код.
3 Выполнить сложение чисел А и В в прямом, обратном и дополнительном коде. Проверить правильность выполнения переводом ответа в десятичное представление.
4 Выполнить сложение чисел С и D в двоично-десятичном коде. Проверить правильность выполнения переводом ответа в десятичное представление.
Таблица 2.5 – Таблица вариантов
| Вариант | A | B | C | D |
| -15 | ||||
| -53 | ||||
| -41 | ||||
| -27 | ||||
| -99 | ||||
| -36 | ||||
| -18 | ||||
| -55 | ||||
| -32 | ||||
| -11 | ||||
| -81 | ||||
| -76 | ||||
| -56 | ||||
| -100 | ||||
| -66 |
Контрольные вопросы
1 Для представления каких чисел чаще всего используется прямой код? Назовите недостатки прямого кода
2 Как осуществить перевод чисел в обратный код?
3 Как выполняется операция вычитания в обратном коде?
4 Как осуществить перевод отрицательного числа в дополнительный код?
5 Каковы достоинства и недостатки дополнительного кода?
6 Что собой представляет двоично-десятичный код числа?
7 По какой причине в двоично-десятичном коде существуют запрещенные комбинации битов?
Практическое занятие № 3
«Изучение принципов построения и работы логических узлов ЭВМ»
Цель работы: изучить основные логические операции и логические элементы, изучить принципы построения схем простых логических узлов.
Студент должен
уметь:
составлять схему и таблицу истинности логического узла согласно заданной формуле;
знать:
основные логические операции и логические элементы, их условные обозначения и таблицы истинности.
Краткие теоретические и учебно-методические материалы по теме практической работы
Логическими элементами называются функциональные устройства, с помощью которых реализуются элементарные логические функции. Они используются для построения сложных преобразователей цифровых сигналов.
К основным логическим элементам относятся элементы «не», «или», «и» «исключающее или».
Элемент «не» – инвертор – реализует функцию логического отрицания. Сигнал на выходе этого элемента равен «1», когда на входе «0».

Рисунок 3.1 – Условно-графическое изображение элемента «не»
 . .
| (3.1) |
Таблица 3.1 – Таблица истинности элемента «не»
| a | Y |
Элемент «или» – реализует функцию логического сложения (дизъюнкции). Сигнал на выходе этого элемента равен «0» тогда и только тогда, когда на обоих входах «0».

Рисунок 3.2 – Условно-графическое изображение элемента «или»
 . .
| (3.2) |
Таблица 3.2 – Таблица истинности элемента «или»
| a | b | Y |
Элемент «и» – реализует операцию логического умножения (конъюнкции). Сигнал на выходе этого элемента равен «1» тогда и только тогда, когда на обоих входах «1».

Рисунок 3.3 – Условно-графическое изображение элемента «и»
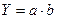 . .
| (3.3) |
Таблица 3.3 – Таблица истинности элемента «и»
| a | b | Y |
Элемент «исключающее или» – «сложение по модулю 2» – сигнал на выходе этого элемента равен «0» тогда и только тогда, когда на обоих входах одинаковые сигналы.

Рисунок 3.4 – Условно-графическое изображение элемента «исключающее или»
Таблица 3.4 – Таблица истинности элемента «исключающее или»
| a | b | Y |