Тема 7
Расчет прочности и жесткости простых балок.
Лекция №9
9.1 Основные гипотезы. Расчетная модель стержня.
9.2 Вывод формул для нормальных напряжений в поперечных сечениях
9.3 Связь между изгибающим моментом и кривизной элемента стержня.
9.4 Чистый плоский изгиб, нормальные напряжения.
Основные гипотезы. Расчетная модель стержня.
Рассмотрим задачу определения нормальных напряжений 
в произвольной точке К поперечного сечения прямого стержня в общем случае его нагружения (рис. 9.1). Наряду с напряжение на площадках параллельных оси стержня развиваются напряжения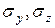 
. Однако опыт показывает, что на основной части длины стержня эти напряжения, как правило, бывают значительно меньше напряжений . Поэтому в расчетной модели стержня пренебрегаем влиянием напряжений 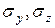на деформацию элемента, т.е. в формуле обобщенного закона Гука для 
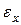получаем:
| 
| 
| 
| (9.1) |
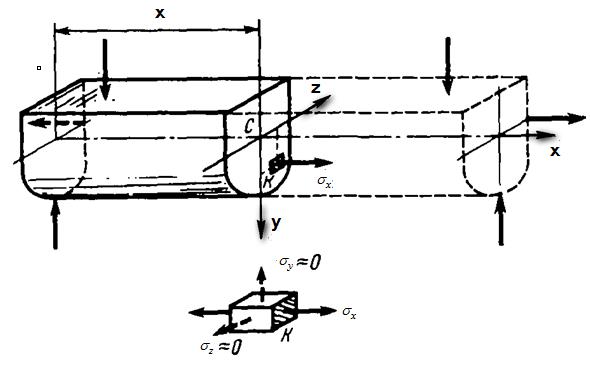
Рис. 9.1 Напряжения 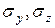малы по сравнению с
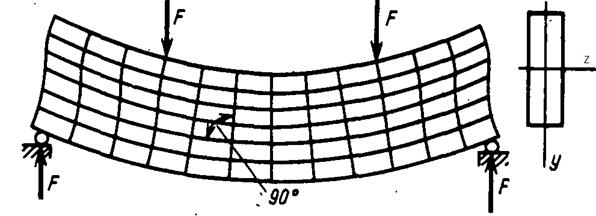
Рис. 9.2 Иллюстрация к гипотезе плоских сечений
Допущение (9.1) называют гипотезой о ненадавливании продольных волокон:
волокна стержня, параллельные его оси, испытывают деформацию растяжения – сжатия в продольном направлении и не оказывают давления друг на друга в поперечном направлении.
Вторая важнейшая гипотеза о характере деформирования модели стержня это гипотеза плоских сечений (рис. 9.2 ):
поперечные сечения балки, плоские до деформации, остаются плоскими и перпендикулярными искривленной оси балки после деформации.
Это положение позволяет рассматривать поперечное сечение стержня как бесконечно тонкое плоское тело (жесткая пластика), имеющее в отношении перемещений конечное число степеней свободы. На рис.9.3, а-в показаны три характерных перемещения сечения (с координатой x): продольное поступательное перемещение 
и два поворота на углы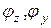 
.
Рис. 9.3 Три независимых перемещения плоского сечения и перемещение точки К от поворота на угол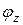 
На рис. 9.3, г показана проекция сечения, повернутого на угол 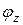при взгляде на сечение вдоль оси z. Произвольная точка К, имеющая координату y >0, получит отрицательное перемещение 
(
), так как это перемещение противоположно оси x. Суммарное перемещение произвольной точки К определится по формуле:
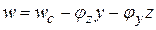
| (9.2) |
Формула (9.2) есть математическое выражение гипотезы плоских сечений. На рис. 9.4, а представлена модель стержня, иллюстрирующая гипотезу ненадавливания продольных волокон и гипотезу плоских сечений.
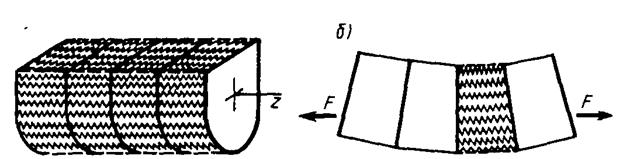
Рис. 9.4 Модель стержня
Модель представляет набор жестких пластинок – «поперечных сечений», пространство между которыми заполнено «продольными волокнами», условно изображенными в виде упругих пружин. Деформация растяжения – сжатия продольных волокон происходит за счет относительного перемещения и поворота соседних сечений (рис 9.4, б).
Вывод формул для нормальных напряжений в поперечных сечениях
Пусть в рассматриваемом сечении известны усилия: 
. Выразим через них напряжения . С учетом формул (9.1), (9.2), (3.6) получим:
| (9.3) |
Обозначим для данного сечения постоянные:
 ;
|  ;
|  .
| (9.4) |
Перепишем (9.3) с учетом обозначений (9.4)
| (9.5) |
Формула (9.5) показывает, что изменяется по закону плоскости, определяемой тремя константами: 
. Для определения констант необходимо потребовать, чтобы приводились к трем силовым факторам (см. формулы 1.2)
| 
| 
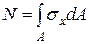
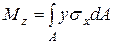
| (9.6) |
Формулы (9.6) следуют из рис. 9.4
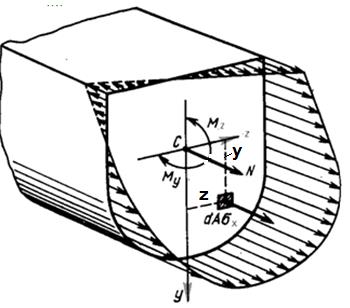
Рис. 9.4 Напряжения в поперечном сечении распределены по линейному закону
Подставляем последовательно выражение для напряжений(9.5) в формулы (9.6). В результате получим:
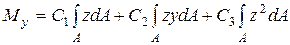
| (9.7) |
С учетом выражений для геометрических характеристик поперечных сечений будем иметь:
 ;
 ;
 .
| (9.8) |
В уравнениях (9.8) введены следующие обозначения: площадь и статические моменты площади относительно осей z и y
A=  ;
|  ;
|  ;
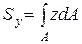| (9.9) |
осевые и центробежный моменты инерции
 ;
|  ;
|  .
| (9.10) |
Будем считать, что оси z,y главные центральные оси, тогда
 .
| (9.11) |
В результате система (9.8) распадается на три независимых уравнения, из которых находим:
| 
| 
| (9.12) |
Подстановка выражений (9.12) в формулу (9.5) дает общую формулу для нормальных напряжений
  y+  z
| (9.13) |
Плоскости z-x, y-x, содержащие ось стержня и одну из главных осей сечения, называются главными плоскостями изгиба стержня.
В формуле (9.13) растягивающая продольная сила N положительна, изгибающие моменты 
также положительны, если они в точке, принадлежащей первой четверти осей координат (где z>0,y>0), вызывают растягивающие напряжения (см.рис.9.4).