III. Формула полной вероятности.
Вероятности гипотез (формула Байеса)
Если событие А может наступить лишь с одним из событий (гипотез) 
попарно несовместных и образующих полную группу событий, то вероятность события А определяется по формуле полной вероятности:
.
Если событие А наступило, то условные вероятности гипотез вычисляются по формулам Байеса:
.
Пример:
На проверку поступают изделия. Каждое из них стандартно с вероятностью 0,9 и нестандартно с вероятностью 0,1. При контроле стандартное изделие принимается с вероятностью 0,95 и отбраковываются с вероятностью 0,05. Нестандартное изделие бракуется с вероятностью 0,9 и принимается с вероятностью 0,1. Найти вероятность того, что поступившее на проверку изделие не будет забраковано.
Обозначим через А событие: поступившее на проверку изделие не будет забраковано, а через В1(В2) событие: поступившее на проверку изделие стандартно (нестандартно). События В1, В2 несовместны и образуют полную группу событий. По формуле полной вероятности имеем
Р(А)=Р(А/ВI)×Р(ВI)+Р(А/В2)×Р(В2)=0,95×0,9+0,1×0,1=0,065.
Пример:
В первой урне 7 белых и 3 черных шара, во второй 8 белых и 4 черных, в третьей 2 белых и 13 черных. Из урн наугад выбирается одна. Какова вероятность того, что: а) шар, взятый наугад из выбранной урны, окажется белым? б) из трех урн была выбрана первая урна, если шар, взятый наугад, оказался белым?
Решение:
а) Пусть Нi – гипотезы о том, что из урн выбрали первую, вторую или третью урну соответственно. Гипотезы попарно несовместны. Тогда
Р(Н1) = Р(Н2) = Р(Н3) = 
.
Условные вероятности доставания из соответствующей урны белого шара: Р(А/Н1) = 
, Р(А/Н2) =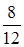 
, Р(А/Н3) = 
.
Тогда по формуле полной вероятности найдем вероятность появления в результате белого шара:
Р(А) = Р(А/Н1) Р(Н1) + Р(А/Н2) Р(Н2) + Р(А/Н3) Р(Н3) = ( + + 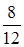) = 0.5
б) По формуле Байеса найдем вероятность того, что из трех урн была выбрана первая урна, если шар, взятый наугад, оказался белым:
Р(Н1/А) = 
= = 
= 
Пример:
Два игрока поочередно бросают монету. Выигрывает тот, у которого раньше выпадет герб. Какова вероятность выигрыша для игрока, бросающего монету первым? Вторым?
Решение:
Пусть А и В - случайные события, состоящие в том, что выигрывает первый и, соответственно, второй игрок, а х и (1- х) – вероятности этих событий. Введем две гипотезы:
Н1 – при первом подбрасывании монеты выпадет герб,
Н2 – при первом подбрасывании монеты выпадет решка.
Тогда Р(Н1) = Р(Н2) = 0.5, а Р(А/Н1) = 1, Р(А/Н2) = Р(В) = 1-х.
По формуле полной вероятности имеем
Р(А) = Р(А/Н1) Р(Н1) + Р(А/Н2) Р(Н2)
Или
х = 1·0.5 + (1-х)·0.5, откуда х =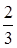 
.
Пример:
Изделия проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Изделие при проверке было признано стандартным. Найти вероятность того, что его проверил второй товаровед.
Обозначим через А событие: изделие при проверке признано стандартным, а через В1 и В2 соответственно события: изделие проверил первый и второй товаровед соответственно. Нам нужно найти вероятность Р(В2/А). Ясно, что В1 и В2 – несовместные события, образующие полную группу событий. По формуле Байеса имеем:
= 
= 
= 
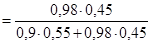=0,471.
Задание на дом
Задача 1.
На распределительной базе находятся электрические лампочки, произведенные двумя заводами. Среди них 70% изготовлены первым заводом и 30% - вторым. Известно, что из каждых 100 лампочек, произведенных первым заводом, 90 штук удовлетворяют стандарту, а из 100 штук, произведенных вторым заводом, удовлетворяют стандарту 80 штук. Определить вероятность того, что взятая наудачу с базы лампочка будет удовлетворять требованиям стандарта.
Ответ: 0,87.
Задача 2.
На сборку поступают детали с трех автоматов. Первый выпускает 20%, второй – 30%, третий – 50% деталей данного типа. Первый автомат дает 0,2% брака, второй – 0,3%, третий – 0,1%. Найти вероятность поступления на сборку бракованной детали.
Ответ: 0,0018.
Задача 3.
На двух автоматических станков изготовляются одинаковые детали. Известно, что производительность первого станка в два раза больше, чем второго, и что вероятность изготовления детали высшего качества на первом станке равна 0,99, а на втором 0,96. Изготовленные за смену на обоих станках нерассортированные детали находятся на складе. Определить вероятность того, что наудачу взятая деталь: а) окажется высшего качества; б) оказавшаяся высшего качества, изготовлена на первом станке.
Ответ: а) 0,98; б)0,673.
Задача 4.
Известно, что 96% выпускаемой продукции удовлетворяет стандарту. Упрощенная схема контроля признает пригодной стандартную продукцию с вероятностью 0,98 и нестандартную с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.
Ответ: 0,998.
IV. Повторные независимые испытания
Если вероятность появления события А в каждом из n независимых опытов постоянна и равна p,а не наступление события А в опыте q = 1 – p, то вероятность наступления события А точно k раз определяется по формуле Бернулли:
Наивероятнейшее число m0 наступлений событий А определяются из неравенства
Пример:
Игральную кость бросили 4 раза. Найти вероятность того, что шестерка выпала ровно 2 раза.
Решение:
Вероятность выпадения шестерки при каждом отдельном бросании кости равна р=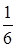 
и поскольку в этой задаче n=4, k=2, 
, искомая вероятность равна
.
Пример:
Сколько раз нужно подбросить игральную кость, чтобы наивероятнейшее выпадение тройки было ровно10?
Решение:
Пусть р= ,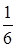 
, тогда по формуле нахождения наивероятнейшего числа: 
или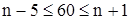 
, т.е. необходимо подбросить кость 
раз.
Пример
При данном технологическом процессе 85% всей продукции высшего качества. Найти наивероятнейшее число изделий высшего сорта в партии из 150 изделий.
По условию n = 150, p = 0,85, q = 1-0,85 = 0,15. Тогда согласно равенству (20), имеем
150×0,85 – 0,15 £ m0 £ 150×0,85 + 0,85,
откуда
127,35 £ m0 £ 128,35.
Следовательно, наивероятнейшее число изделий высшего сорта в партии из 150 изделий при данном технологическом процессе, равно 128.
Пример
Вероятность того, что покупатель будет обслужен в течении 5 минут, равна 
. Определить наиболее вероятное число покупателей, обслуженных в течении 5 минут, из группы в 13 человек.
По условию n = 13, p =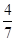 
, q = 1- = 
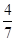. Следовательно, из неравенства (20), следует
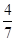13× - £ m0 £ 13× 
,
или
7 £ m0 £ 8.
Это означает, что имеется два значения: m0' = 7 и m0"= 8, каждое из которых является наиболее вероятным числом обслуженных покупателей.
Пример:
Стрелок стреляет по мишени до тех пор, пока общее число промахов не станет равным 3. Вероятность промаха при одном выстреле равна 0.2. Какова вероятность того, что стрелок израсходует ровно 7 патронов.
Решение:
По условию задачи последний, седьмой выстрел должен дать промах, остальные два промаха могут произойти произвольно в предыдущих 6 выстрелах. Тогда вероятность того, что стрелок израсходует ровно 7 патронов, равна:
Р(А) = q·С62 р2 q4 = 
= 0.04915
Задание на дом
Задача 5.
Последовательно посланы четыре радиосигнала. Вероятность приема каждого из них не зависит от того, приняты ли остальные сигналы, и равна 0,3. Определить вероятность приема 1,2,3,4 сигналов, а также ни одного из них.
Ответ: 0,4116; 0,2646; 0,0756; 0,0081; 0,2401.
Задача 6.
Среди изготовленных рабочими деталей в среднем бывает 4% брака. Какова вероятность того, что среди среди взятых на испытание 6 деталей 2 будут бракованными?
Ответ: 0,029.
Задача 8.
Для данного баскетболиста вероятность забросить мяч в корзину при одном броске равна 0,4. Произведено 10 бросков. Найти наивероятнейшее число попаданий.
Ответ: 4.