Политехнический университет
Факультет прикладной математики и механики
Кафедра прикладной математики
РАСЧЕТНАЯ РАБОТА по дисциплине
«Теория риска и моделирование рисковых ситуаций»
Выполнил:
студент группы МИЭ-17-1м
Паршаков Роман Владимирович
Проверил:
доцент кафедры ПМ, к.ф.-м.н.
Севодин Михаил Алексеевич
ПЕРМЬ, 2019
Задание 1
Вероятности условий хозяйственных ситуаций составляют: 0,2 - для ситуации А 1; 0,3 - для ситуации А 2; 0,5 - для ситуации А 3.
Таблица 1
Норма прибыли на вложенный капитал
| Варианты рискового вложения капитала | Условия хозяйственной ситуации | ||
| А 1 | А 2 | А 3 | |
| К 1 К 2 К 3 | 50% 40% 30% | 60% 30% 40% | 70% 20% 50% |
Определите степень риска для каждого из мероприятий. Сделайте выводы.
Решение:
Для принятия решения о выборе варианта вложения капитала необходимо знать величину риска и сопоставить её с нормой прибыли на вложенный капитал.
В данном случае величину риска можно определить как разность между показателями нормы прибыли на вложенный капитал, получаемыми на основе точных данных об условиях хозяйственной ситуации, и ориентировочными показателями (Таблица 2):
Таблица 2
Величина рисков для разных вариантов рискового вложения капитала
| Варианты рискового вложения капитала | Хозяйственные ситуации | ||
| А 1 | А 2 | А 3 | |
| К 1 К 2 К 3 | 50-30=20% 40-30=10% 30-30=0% | 60-30=30% 30-30=30% 40-30=10% | 70-20=50% 20-20=0% 50-20=30% |
Выбор варианта вложения капитала в условиях неопределенности хозяйственной ситуации зависит, прежде всего, от степени этой неопределенности.
В нашем случае, выбор варианта вложения капитала производится при условии, что вероятности условий хозяйственных ситуаций известны.
Вычислим среднее ожидаемое значение нормы прибыли на вложенный капитал для каждого варианта вложения капитала:
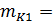0,2*50+0,3*60+0,5*70=63%
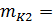0,2*40+0,3*30+0,5*20=27%
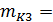0,2*30+0,3*40+0,5*50=43%
Вычислим средние квадратичные отклонения нормы прибыли для каждого варианта вложения капитала:
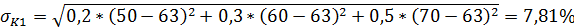
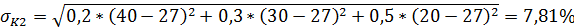
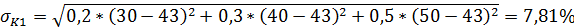
Вычислим значения коэффициентов вариабельности для каждого варианта вложения капитала:
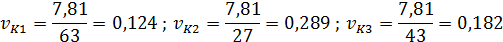
Вывод: следует выбрать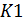 
вариант вложения, ибо при равных средних квадратичных отклонениях для всех вариантов математическое ожидание для варианта 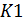является наибольшим, а также данный вариант обладает наименьшей вариабельностью, то есть рискованностью.
Задание 2
Директор лицея, обучение в котором осуществляется на платной основе, решает, следует ли расширять здание лицея на 250 мест, на 50 мест или не проводить строительных работ вообще. Если население небольшого города, в котором организован платный лицей, будет расти, то большая реконструкция могла бы принести прибыль 250 тыс. руб. в год, незначительное расширение учебных помещений могло бы приносить 90 тыс. руб. прибыли. Если население города увеличиваться не будет, то крупное расширение обойдется лицею в 120 тыс. руб. убытка, а малое — 45 тыс. руб. Однако информация о том, как будет изменяться население города, отсутствует.
Пусть при тех же исходных данных государственная статистическая служба предоставила информацию об изменении численности населения: вероятность роста численности населения составляет 0,7; вероятность того, что численность населения останется неизменной или будет уменьшаться, равна 0,3. Какова ожидаемая ценность дополнительной информации?
Решение:
Представим исходные данные в виде таблицы выигрышей (потерь):
| Номер стратегии | Действия компании | Выигрыш, тыс. руб. при состоянии демографической ситуации | |
| благоприятном | неблагоприятном | ||
Расширять здание лицея на 250 мест ( )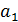
| |||
Расширять здание лицея на 50 мест ( )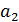
| |||
Не проводить строительных работ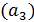 
|
Примечание. Вероятность благоприятного и неблагоприятного состояния демографической ситуации равна 0,5.
Рассчитаем ожидаемые денежные оценки при отсутствии точной информации:
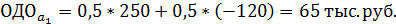
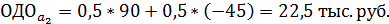
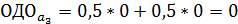
Максимальная ожидаемая денежная оценка в этом случае равна:
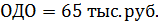
Рассчитаем ожидаемые денежные оценки при наличии точной информации (вероятности благоприятной и неблагоприятной ситуации равны 0,7 и 0,3 соответственно):
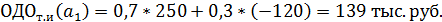
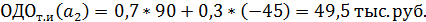
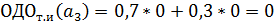
Максимальная ожидаемая оценка точной информации равна:
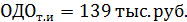
Тогда ожидаемая ценность точной (дополнительной) информации равна:
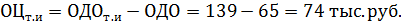
Значение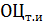 
показывает, какую максимальную цену должен быть готов платить директор лицея за точную (дополнительную) информацию об истинном состоянии демографической ситуации в городе в тот момент, когда ему это необходимо.
На основе исходных данных можно построить дерево решений Рис.1:
| 250 000 |
| -45 000 |
| 90 000 |
| -120 000 |
| 250 000 |
| -45 000 |
| 90 000 |
| -120 000 |
| Учитывать дополнительную информацию |
| Неблагоприятное состояние (0,30) |
| Благоприятное состояние (0,70) |
| Неблагоприятное состояние (0,30) |
| Благоприятное состояние (0,70) |
| Не проводить строительных работ |
| Расширение лицея на 50 мест |
| Расширение лицея на 250 мест |
| Неблагоприятное состояние (0,50) |
| Благоприятное состояние (0,50) |
| Неблагоприятное состояние (0,50) |
| Благоприятное состояние (0,50) |
| Не проводить строительных работ |
| Не учитывать дополнительную информацию |
| Расширение лицея на 250 мест |
| Расширение лицея на 50 мест |
| * |
| * |
| * |
| * |
| * |
| 65 000 |
| 22 500 |
| 139 000 |
| 49 500 |
| 65 000 |
| 139 000 |
Рис.1. Дерево решений
Задание 3
Найти наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы — выигрыши):
A=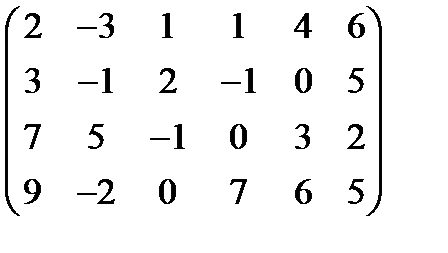 
Решение:
Матрица рисков R будет иметь вид:
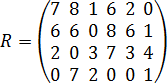
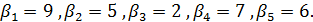
Критерий максимакса.
M=9, следовательно наилучшее решение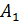 
.
Максиминный критерий Вальда.
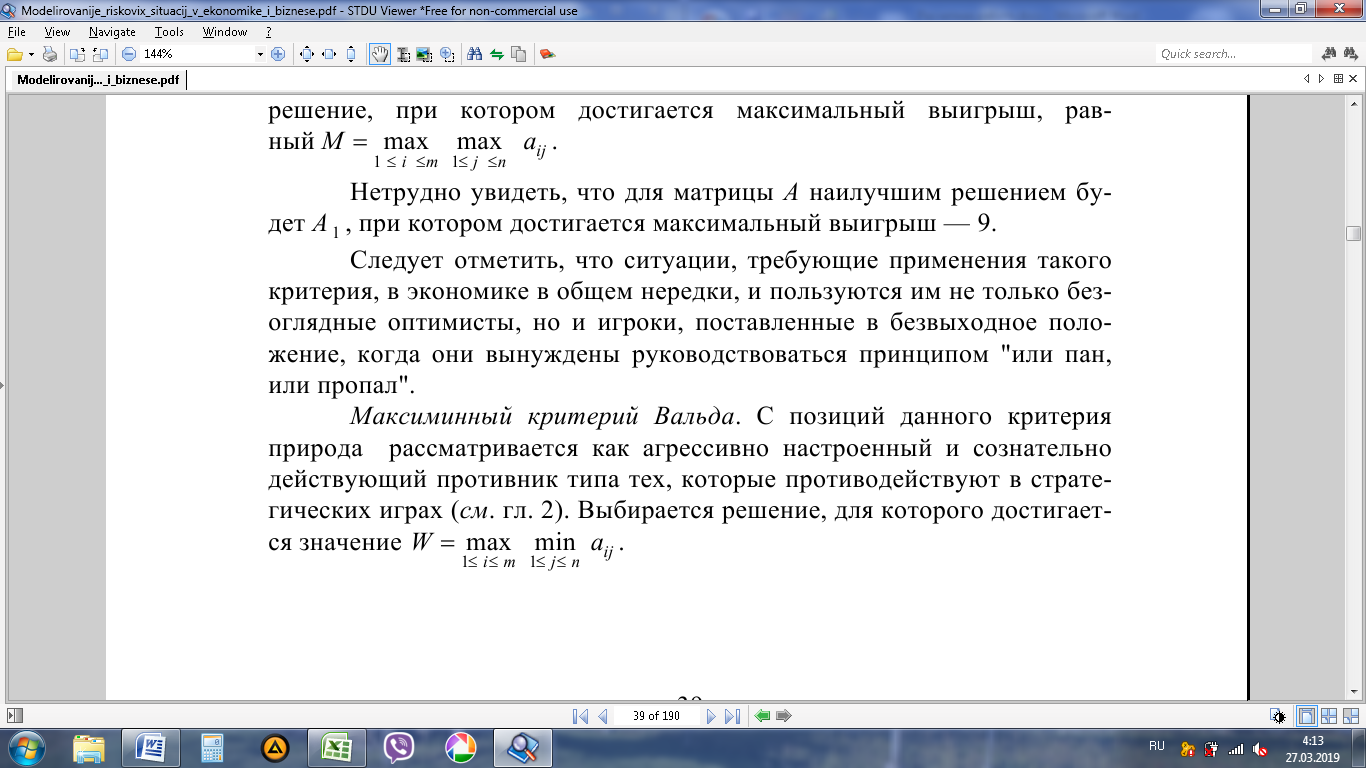
для первой стратегии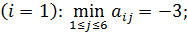 
для второй стратегии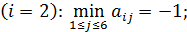 
для третьей стратегии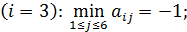 
для четвертой стратегии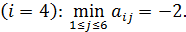 
Тогда W=-1, что соответствует стратегии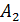 
и 
.
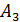Критерий минимаксного риска Сэвиджа.
для первой стратегии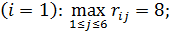 
для второй стратегии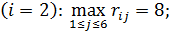 
для третьей стратегии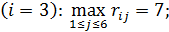 
для четвертой стратегии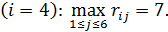 
Минимально возможный из самых крупных рисков, равен 7, достигается при использовании третьей 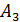и четвертой 
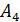стратегий.
Критерий пессимизма-оптимизма Гурвица.
Для матрицы A (p=0,2):
для первой стратегии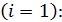 
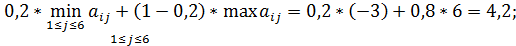
для второй стратегии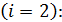 
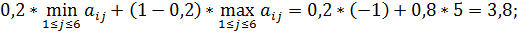
для третьей стратегии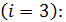 
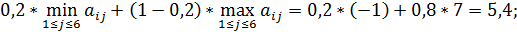
для четвертой стратегии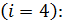 
Тогда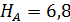 
, то есть оптимальной является четвертая стратегия .
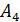Для матрицы рисков R (p=0,4):
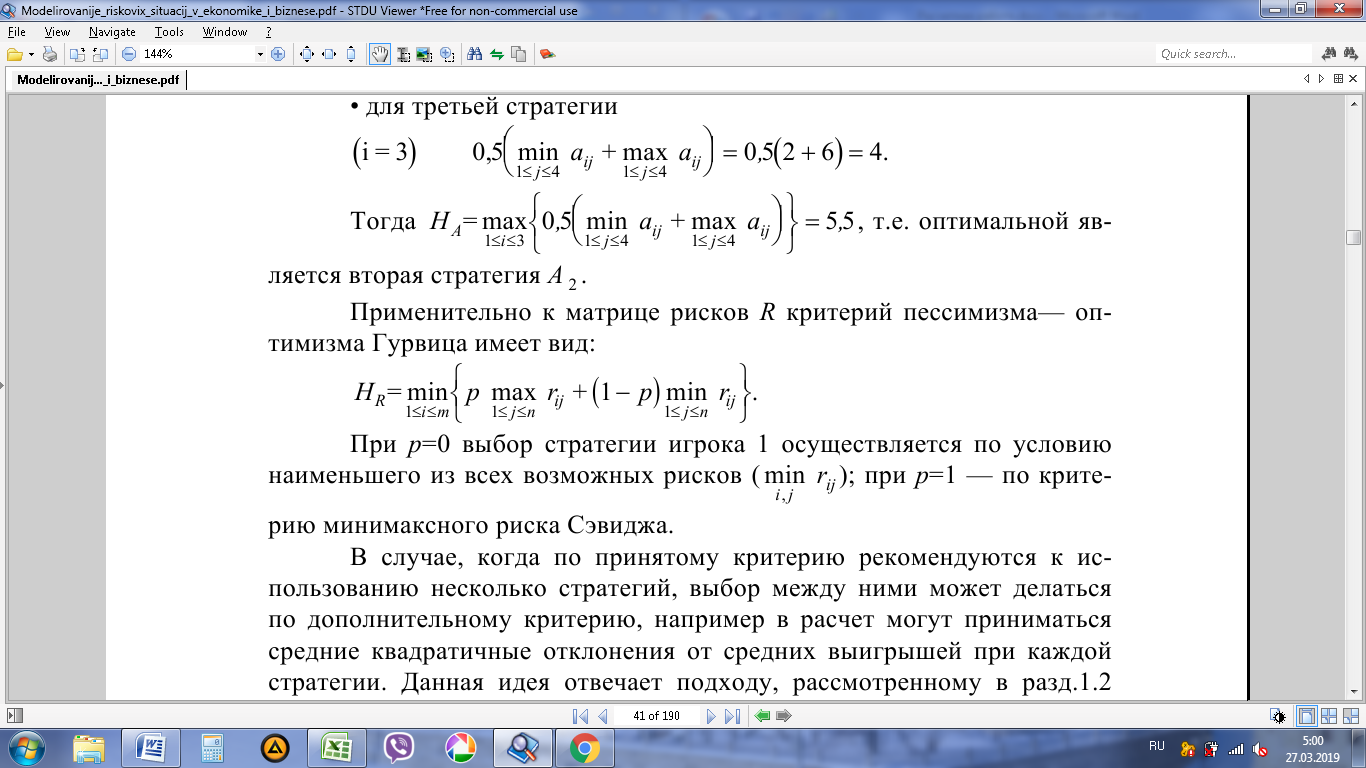
для первой стратегии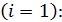
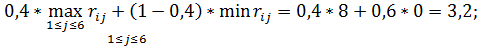
для второй стратегии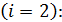
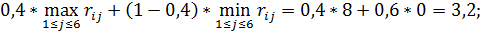
для третьей стратегии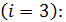
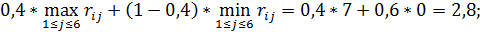
для четвертой стратегии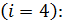
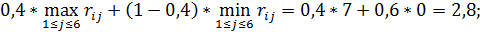
Тогда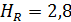 
, то есть оптимальной является третья 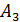и четвертая 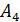стратегии.
Проведем анализ полученных результатов. Для игрока 1 лучшими являются стратегии:
· По критерию максимакса: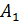
· По максиминному критерию Вальда: 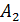и
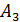
· По критерию минимаксного риска Сэвиджа: 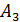и
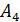
· По критерию пессимизма-оптимизма Гурвица для матрицы A (при p=0,2):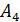
· По критерию пессимизма-оптимизма Гурвица для матрицы R (при p=0,4): 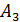и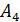
Поскольку стратеги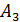и и 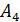фигурирует в качестве оптимальных по трем критериям выбора из пяти испытанных, степень их надежности можно признать достаточно высокой для того, чтобы рекомендовать эти стратегии к практическому применению.