Силы тяготения
Все физические тела испытывают действие сил взаимного тяготения.
Основной закон был сформулирован Ньютоном: Между двумя телами, массы которых m1 и m2, находящихся на расстоянии r, действуют силы взаимного притяжения F12 и F21, направленные от данного тела к другому телу, причем модуль силы тяготения пропорционален произведению масс тел и обратно пропорционален квадрату расстояния между ними
,
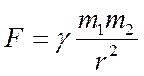где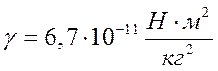 
- гравитационная постоянная.
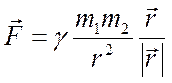
Здесь массы точечные. Шарообразные тела со сферически симметричным распределением массы в их объеме взаимодействуют так же, как если бы их массы были сосредоточены в центрах шаров.
Заметим, что силы тяготения потенциальны, т.е. не зависят от пути (работы в поле сил не зависят от пути).
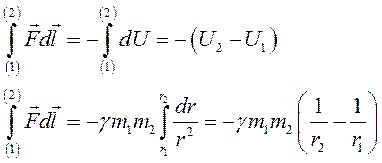
Потенциальная энергия материальной точки m1 в поле точки m2 записывается так:
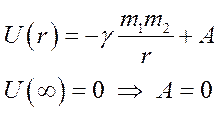
То же для m2 в поле m1.
Поле У поверхности Земли
Для тел, находящихся на высоте h, запишем:
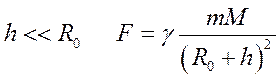, где 
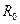- радиус Земли.
Применим разложение
.
.
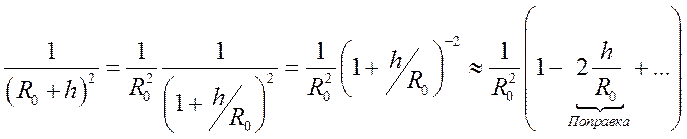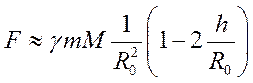Тогда для высоты полета самолета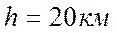 
, и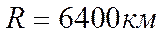 
, имеем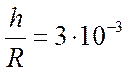 
С этой точностью можно считать, что F=const в близи поверхности Земли.
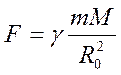(1)
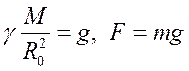
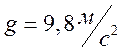- ускорение силы тяжести к поверхности Земли. В таком приближении рассмотрено много задач, связанных с силой тяжести.
Гравитационная энергия шарообразного тела
Потенциальная энергия в точке В равна: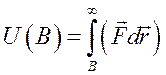 
.
По закону сохранения энергии сумма кинетической и потенциальной энергии постоянна.
Вычислим гравитационную энергию шарообразного тела. Имеем шар радиуса R и массой M. Энергия гравитационного поля численно равна работе, которую необходимо затратить, чтобы частицы шара развести на бесконечное расстояние друг от друга.
Для упрощения примем, что шар однородный, его плотность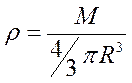 
.
Сначала рассмотрим энергию твердого шарового ядра с радиусом r и окружающего его шарового слоя, т.е. сферы толщина которой dr.
Масса центрального шара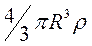 
, масса слоя 
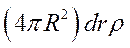. Работа удаления шарового слоя толщиной dr равна потенциальной энергии шарового слоя в гравитационном поле, созданном всеми внутренними слоями (т.е. шаровым ядром радиуса r):
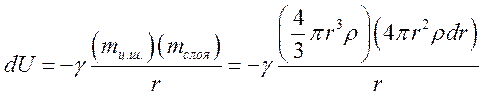(2)
Гравитационная энергия шара радиуса R выразится
.
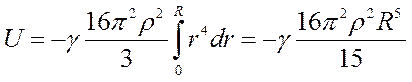Так как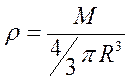 
, то
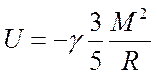(3).
Эта энергия, которая связана с гравитационным взаимодействием частиц шара.
Например, собственная энергия Солнца:
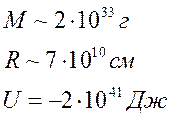
Вычислим напряженность гравитационного поля внутри и вне шара радиуса R, заполненного веществом с постоянной объемной плотностью.
. 
.
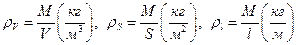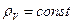Определим напряженность (g) гравитационного поля вне шара.
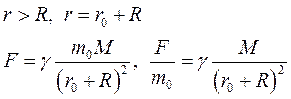
Если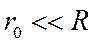 
, то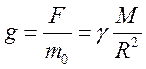 
.
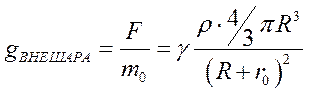- с увеличением расстояния от центра шара напряженность убывает, и создается массой всего шара радиуса R.
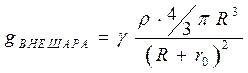
Напряженность внутри шара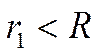 
.
Оказывается, что напряженность внутри шара возрастает и создается только веществом шара, заключенным в сфере радиуса r 1. То есть, на гравитационное поле не влияет вещество, расположенное вне вспомогательной сферы!!!
Доказать это самостоятельно.
Гравитационный радиус
Энергия покоя тела массы M равна Mc 2. Не является ли эта энергия энергией гравитационного поля, превратившейся в энергию массы покоя при стягивании частиц тела из бесконечности. Вычислим, радиус шара, которому соответствует эта энергия.
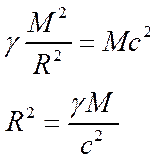
Для Земли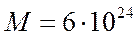 
кг и получаем 
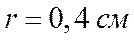. Но фактически 
.
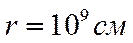То есть, в общем балансе энергии гравитационная энергия земли играет малую роль.
Размеры Вселенно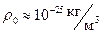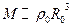й 
, 
и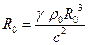 
. Иначе, 
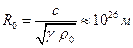, т.е. радиус примерно соответствует радиусу Вселенной.
Движение искусственных спутников Земли.
При выводе первой космической скорости не будем учитывать:
- Сопротивление воздуха.
- Притяжение Солнца и планет.
Выгодно использовать скорость вращения Земли – запускать спутник в направлении вращения Земли, то есть с Запада на Восток.
Первая космическая скорость – скорость полета по круговой орбите с радиусом, равным радиусу Земли.
Полная энергия спутника в поле Земли:
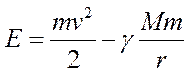(1)
Считаем, что напряженность поля зависит от расстояния до центра Земли:
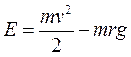(2)
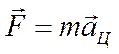- движение равномерное.
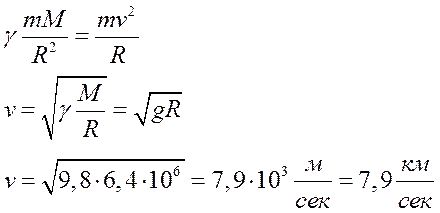
Движение финитно.
Вторая космическая скорость – скорость у поверхности Земли, позволяющая покинуть пределы земного притяжения.
Минимальная полная энергия, при которой движение становится инфинитно равна 0. Иначе говоря, кинетическая энергия тела равна потенциальной.
Из (1) получаем:
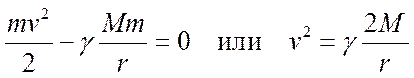. Т.к. 
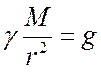имеем
.
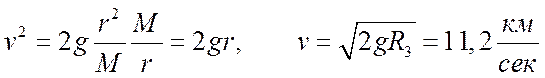Третья космическая скорость – скорость тела, находящегося на орбите Земли, которая необходима для того, что бы покинуть пределы Солнечной системы.
Если полная энергия положительна, т.е. начальная скорость больше второй космической, то спутник навсегда покидает область притяжения Солнца – третья космическая скорость.
Третья космическая скорость зависит от направления. Она минимальна, если направление совпадает с направлением движения по орбите Земли вокруг Солнца.
Из (1) следует:
Замечания:
1. Земля не является шаром, то есть ее поле тяготения – не поле тяготения точечной массы.
2. Земная атмосфера тормозит движения спутника Земли.
Эффект скручивания