Тема 7
Расчет прочности и жесткости простой балки
Лекция №14
Перемещения при изгибе
14.1 Учет симметрии при определении перемещений.
14.2. Решение дифференциальных уравнений оси изогнутой балки способом выравнивания постоянных интегрирования.
14.3 Особенности расчета консольной балки.
14.4 Поверочный расчет прочности и жесткости балки на ПЭВМ
Учет симметрии при определении перемещений.
При симметричной расчетной схеме балки и симметричной нагрузке эпюра прогибов симметричная, а эпюра углов поворота сечений кососимметричная. Рассмотрим шарнирно опертую балку, загруженную в середине пролета сосредоточенной силой 
(рис.14.1) Легко видеть, что максимальный прогиб 
возникает в середине пролета балки, следовательно, угол поворота 
Рис. 14.1 Учет симметрии при определении перемещений
Таким образом, достаточно записать уравнения для функции прогибов и функции углов поворота сечений только на первом участке:
| 
| 
| 
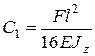
| (14.1) |
На левой опоре прогиб равен нулю;
 ,
|  ,
|  .
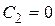| (14.2) |
Окончательно:
| 
| (14.3) |
14.2. Решение дифференциальных уравнений оси изогнутой балки способом выравнивания постоянных интегриро вания.
Определяем опорные реакции в балке от действия нормативных нагрузок.
Задаемся общим для всех участков загружения началом координат 
, 
на левом конце балки или на правом. На каждом участке составляем дифференциальное уравнение оси изогнутой балки
 ,
| (14.3) |
где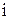 
– номер участка, 
– изгибная жесткость балки. Интегрируя дифференциальное уравнение (14.3), получим уравнение тангенсов углов наклона касательной к оси изогнутой балки (углов поворота сечений)
| (14.4) |
а, интегрируя второй раз, – уравнение прогибов
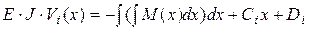
| (14.5) |
Здесь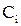 
и 
– постоянные интегрирования.
Для обеспечения равенства постоянных интегрирования (
) на всех участках загружения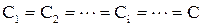 
и 
необходимо руководствоваться следующими правилами:
1. При составлении выражения для изгибающего момента 
всегда рассматривать часть балки, расположенную между началом координат и сечением.
2. Распределенную нагрузку, которая заканчивается на границе участков загружения, продолжать до конца балки с добавлением «компенсирующей» нагрузки противоположного направления («продленную» и «компенсирующие» нагрузки показывать на чертежах штриховыми линиями).
3. Момент пары сил, приложенной к балке на границе участка с координатой 
, при включении в выражение для изгибающего момента умножать на множитель 
, равный единице.
4. Выражения, содержащие множитель вида 
, интегрировать, не раскрывая скобок.
Составив и проинтегрировав в соответствии с этими правилами дифференциальные уравнения на каждом участке, необходимо проверить равенство постоянных интегрирования, используя условия гладкого и непрерывного сопряжения оси балки на границах между участками 
| 
| (14.6) |
Значения постоянных интегрирования C и D находим из условий равенства нулю прогибов в опорных сечениях для шарнирно опертой балки или прогиба и угла поворота сечения в защемлении для консольной балки.
Положительному значению V(x) соответствует перемещение, направленное вниз.
Положительному углу 
соответствует поворот сечения по ходу часовой стрелки, если ось x направлена вправо, или против хода часовой стрелки, если ось x направлена влево.
Пример14.1 Выполнить расчет на жесткость балки, геометрическая схема которой с нормативной нагрузкой представлена на рис. 14.2
Рис. 14.2 Распределенная нагрузка продолжается до конца балки с добавлением компенсирующей нагрузки противоположного направления.
Совместим начало координат осей 
с левым концом балки и разобьем ее на три участка 1, 2 и 3 (см. рис 14.2).
Первый участок. 
.
Дифференциальное уравнение оси изогнутой балки имеет вид
| (14.7) |
Второй участок. 
| (14.8) |
Третий участок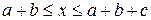 
.
| (14.9) |
Здесь для обеспечения равенства постоянных интегрирования распределенная нагрузка интенсивностью 
продолжена до конца балки и введена компенсирующая нагрузка обратного направления той же интенсивности , а момент сосредоточенной пары 
умножен на фиктивное плечо 
.
Проинтегрировав дважды дифференциальные уравнения (14.7) – (14.9), получим выражения для нахождения углов поворота сечений и прогибов
| (14.10) |
| (14.11) |
| (14.12) |
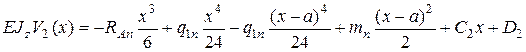
| (14.13) |
| (14.14) |
| (14.15) |
Рассмотрев условия (14.6) гладкого и непрерывного сопряжения оси изогнутой балки на границах участков загружения, получим
 ,
|  .
|  ,
|  .
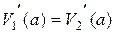| (14.16) |
Таким образом,
 .
| (14.17) |
Для второй группы констант имеем:
 ,
|  .
|  ,
|  .
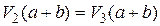| (14.18) |
В результате получаем:
 .
| (14.19) |
Постоянные определяем из условия равенства нулю прогибов в сечениях над опорами:
| 
| (14.20) |
,
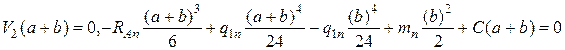| (14.20) |
На рис. 14.3 показана геометрическая схема балки с нагрузкой, когда начало координат принимается на правом конце балки
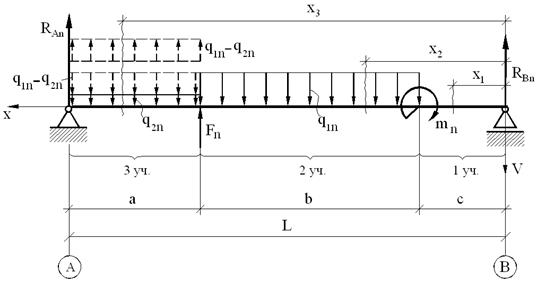
Рис. 14.3 Распределенная нагрузка продолжается до конца балки с добавлением компенсирующей нагрузки, с учетом существующей