Кафедра машиностроения
По дисциплине: МЕХАНИКА
Тема: Решение задач. Задача №4
Выполнил: студент группы РМ-17Конченко А.И.
Проверил: доцентЗлотников Е.Г.
Санкт-Петербург
2019 год

 Дано:
Дано:
a = 1,2 м
b = 1,5 м
c = 0,8 м
P = 5 кН
Марка стали – 30
sт = 300 МПа
nт = 2,5 Рис. 1. Расчетная схема
Е = 2*105 МПа

Задача:
Требуется подобрать сечения стержней по условию их прочности, приняв запас прочности по отношению к пределу текучести nт = 2,5.
Жесткий брус АВ закреплен, как показано на рис. 1, и нагружен силой  5 кН.
5 кН.
Вычислим степень статической неопределимости.
Жесткий брус АВ закреплен с помощью шарнирно-неподвижной опоры и поддерживается двумя деформируемыми стальными стержнями DЕ и ВE. На опоре С (рис.4) - две составляющие реакции XC и YC, реакции в стержнях направлены вдоль их осей и приложены к брусу АВ в точках D и В. Направление этих реакций рекомендуется установить после анализа возможного деформированного состояния конструкции.
Для плоской системы сил в общем случае ее приложения к конструкции можно составить только три независимых уравнения равновесия. В рассматриваемой задаче к брусу АВ приложено четыре неизвестных усилия: две реакции в шарнире и два усилия в стержнях. Разность между числом неизвестных усилий и числом уравнений статики показывает, что для определения этих неизвестных необходимо составить еще одно уравнение статики, в которое входили бы интересующие нас величины. Такое уравнение или несколько подобных уравнений можно получить из геометрических зависимостей между деформациями элементов заданной конструкции.
Рассмотрим конструкцию после деформации ее элементов (рис.2). Под действием силы Р жесткий брус может повернуться вокруг точки С, при этом стержни DЕ и ВE будут деформированы. Точки А и В описывают при повороте бруса дуги окружностей, которые ввиду малости перемещений заменяются касательными, т.е. считается, что эти точки перемещаются по перпендикулярам к радиусам АС и ВС этих дуг. Точка А смещается вниз и занимает положение  , точка В - вверх, занимая положение
, точка В - вверх, занимая положение 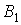 . Брус, как абсолютно жесткий элемент конструкции, - положение
. Брус, как абсолютно жесткий элемент конструкции, - положение  .Очевидно, что стержень DЕ сжат и стал короче на величину DD1 = Dl1. Соединив точки E и
.Очевидно, что стержень DЕ сжат и стал короче на величину DD1 = Dl1. Соединив точки E и 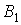 , находим на чертеже положение стержня ВE после его деформации. Опустив перпендикуляр из точки В на прямую B1E, находим точку
, находим на чертеже положение стержня ВE после его деформации. Опустив перпендикуляр из точки В на прямую B1E, находим точку  .
.
|
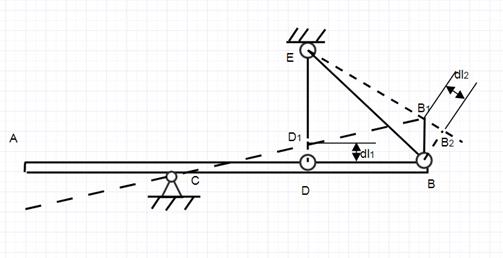
Рис.2. Схема конструкции после деформации
Отрезок  - сжатие стержня ВE.
- сжатие стержня ВE.
Действительно, Dl2 = EB-EB1 = EB2-EB1 так как EВ=EВ2, и стержень EВ сжат.
Выяснив направление усилий в стержнях, составляем уравнение ее равновесия:

Определения составляющих реакции шарнира  для решения данной задачи не требуется, и два других уравнения статики не составляются.
для решения данной задачи не требуется, и два других уравнения статики не составляются.
Для вычисления усилий в стержнях  необходимо иметь еще одно уравнение, называемое уравнением совместности деформаций. Это уравнение получаем из геометрических соотношений между деформациями элементов заданной конструкции. При этом ввиду малости деформаций изменением угла наклона стержня ВE пренебрегаем, считая что Ð
необходимо иметь еще одно уравнение, называемое уравнением совместности деформаций. Это уравнение получаем из геометрических соотношений между деформациями элементов заданной конструкции. При этом ввиду малости деформаций изменением угла наклона стержня ВE пренебрегаем, считая что Ð  .
.
Тогда

Из подобия треугольников DCD1 и B1CB находим соотношение между деформациями стержней -  :
:


Полученная зависимость называется условием совместности деформаций.
Абсолютные удлинения стержней можно выразить через усилия, используя формулу Гука:

Подставив выражения в условие совместности деформаций, получим

Решая систему уравнений, определяем усилия в стержнях  . Для этого подставим значение N1:
. Для этого подставим значение N1:

Решив систему уравнений, получим


Определив усилия в стержнях, переходим к подбору площадей их поперечных сечений.
Для заданного материала вычислим допускаемое напряжение

Определяем напряжения в стержнях и выбираем большее:

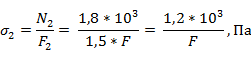
Площадь сечения F подбираем по условию прочности наиболее нагруженного стержня. Так как  больше
больше 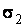 , используем условие прочности первого стержня:
, используем условие прочности первого стержня:


Площади сечений стержней принимаем в соответствии с заданным соотношением:

Ответ: 
