Поверхностные интегралы I и II рода.
Интеграл по площади поверхности (поверхностный интеграл первого рода)
Обобщением двойного интеграла для функции трех переменных приводит нас к понятию поверхностного интеграла, который конструктивно выводится, так же как и криволинейные.
Пусть в некоторой области поверхности S, ограниченной замкнутой кривой L пространства Oxyz определена непрерывная функция f(x,y,z).
Разобьем поверхность S на n частей с площадями  и выберем в каждой из них некоторую точку
и выберем в каждой из них некоторую точку  и составим интегральную сумму:
и составим интегральную сумму:

 (1)
(1)
Определение: Если предел интегральной суммы (1) при n→∞ и 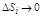 существует и не зависит от способа разбиения поверхности S на части и выбора точек внутри них, то он называется поверхностным интегралом I рода.
существует и не зависит от способа разбиения поверхности S на части и выбора точек внутри них, то он называется поверхностным интегралом I рода.
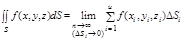
Теорема (существования). Если поверхность S гладкая (т.е. в каждой точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x,y,z) непрерывна на этой поверхности, то поверхностный интеграл I рода существует.
Свойства поверхностного интеграла I рода
1. 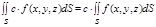 , где с–const.
, где с–const.
2. 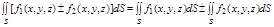
3. Если поверхность S разбить на части 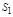 и
и 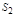 , так, что
, так, что 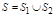 , то
, то
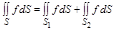
4. 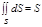 , где S площадь поверхности.
, где S площадь поверхности.
5. 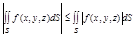
6. Если f(x,y,z) непрерывна на поверхности S, то на этой поверхности существует точка 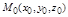 такая, что
такая, что
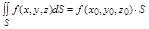
2. Вычисление поверхностного интеграла I рода.
Вычисление поверхностного интеграла I рода, при условии, что поверхность S правильная в направлении оси Oz, сводится к вычислению двойного интеграла по области D, где D проекции поверхности S на плоскость xOy.
Разобьем поверхность S на n части с площадью 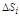 , при i=1,…, n, при этом проекции поверхности S в плоскости xOy так же оказывается разбитой на n частей
, при i=1,…, n, при этом проекции поверхности S в плоскости xOy так же оказывается разбитой на n частей  с площадью каждой
с площадью каждой 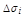 .
.
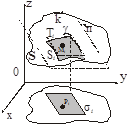 Выберем в произвольном участке
Выберем в произвольном участке  точку
точку  и восстановим перпендикуляр к плоскости xOy, до пересечение с поверхностью S в точке
и восстановим перпендикуляр к плоскости xOy, до пересечение с поверхностью S в точке 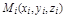 расположенной на участке
расположенной на участке 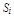 .
.
Построим к точке  касательную плоскостью, и рассмотрим ту её часть
касательную плоскостью, и рассмотрим ту её часть 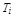 , которая проектируется на плоскость xOy в область
, которая проектируется на плоскость xOy в область  .
.
Обозначим через 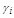 , острый угол между осью Oz и нормалью
, острый угол между осью Oz и нормалью 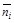 к поверхности в точке
к поверхности в точке  , тогда
, тогда
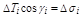 (2)
(2)
Если поверхность S задана уравнение z=z(x,y), то координаты нормального вектора в точке 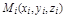 примут вид
примут вид 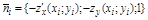 , а острый угол
, а острый угол 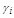 между ортом k={0,0,1} и нормалью
между ортом k={0,0,1} и нормалью  к поверхности S в точке
к поверхности S в точке  , найдём из:
, найдём из:
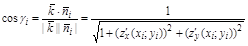
Таким образом равенство (2) примет вид:

и переходя к пределу получим:

Если же поверхность S задана уравнениями y=y(x,y) или x=x(y,z) т.е. правильная соответствие в направлении оси Oy или Ox, то аналогично получим:
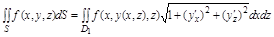

где 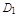 и
и 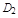 проекции поверхности S в плоскости xOz и yOz соответственно.
проекции поверхности S в плоскости xOz и yOz соответственно.
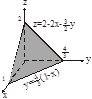 Пример 1. Вычислить
Пример 1. Вычислить 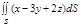 где S часть плоскости 4x+3y+2z–4=0 расположенной в I октане.
где S часть плоскости 4x+3y+2z–4=0 расположенной в I октане.
1. 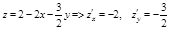
2. 
3. 

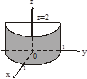 Пример 2. Вычислить
Пример 2. Вычислить 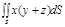 где S часть цилиндрической поверхности
где S часть цилиндрической поверхности 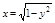 отсекаемой плоскостями z=0, z=2.
отсекаемой плоскостями z=0, z=2.
1. 
2. 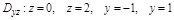
3. 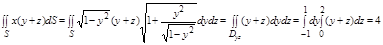
Пример 3. Вычислить  , где S – часть поверхности цилиндра
, где S – часть поверхности цилиндра 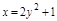 , при y>0, вырезаемая поверхностями
, при y>0, вырезаемая поверхностями 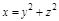 и
и 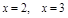 .
.
1. Изобразим искомую поверхность
а. Построим цилиндр 
б. Заменим построение параболоида  построением цилиндра
построением цилиндра 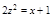 полученного исключением
полученного исключением 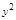 из уравнений
из уравнений 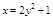 и
и  .
.
2. Поверхность S имеем уравнение 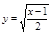 , найдем по проекции на плоскость xOz, это полоса от х=2 до х=3 ограниченный параболой
, найдем по проекции на плоскость xOz, это полоса от х=2 до х=3 ограниченный параболой 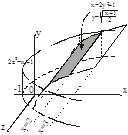

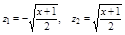
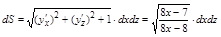
3. 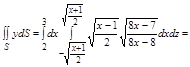


Задача. Вычислить поверхностный интеграл I рода  где
где 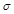 –часть поверхности z=x2+y2, расположенная между плоскостями z=0 и z=1.
–часть поверхности z=x2+y2, расположенная между плоскостями z=0 и z=1.
1. Данная поверхность – часть эллиптического параболоида z=x2+y2, взаимно однозначно проектируется на плоскость xOy в круг x2+y2≤1.
2. Используя уравнение поверхности, находим: z=x2+y2,  =2x,
=2x, 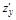 =2y,
=2y,
 .
.

Перейдем к полярным координатам:  ,
, 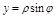 ,
, 
 ;
;  ,
,  ,
, 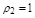 ,
, 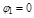 ,
, 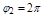
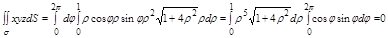
3. Приложение поверхностного интеграла I рода.
а. Площадь поверхности цилиндра.
Если поверхность S задана уравнением z=z(x,y) вместе со своими производными непрерывна в области D плоскости xOy, где D проекция поверхности S, то
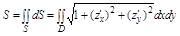
б. Масса поверхности.
Если функция 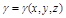 есть функция распределения плотности по поверхности S, то масса поверхности равна
есть функция распределения плотности по поверхности S, то масса поверхности равна

в. Моменты и центры тяжести поверхности.
1. Моменты инерции относительно осей и начала координат:

| 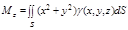
|
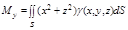
| 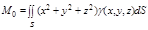
|
2. Статические моменты материальной поверхности S относительно координатных плоскостей.
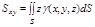
| 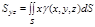
| 
|
3. Координаты центра тяжести материальной поверхности S
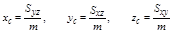
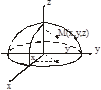 Пример. Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию до оси Oz.
Пример. Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию до оси Oz.
1. 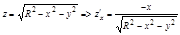 ,
, 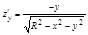
2. 
 , для удобства вычислений перейдём в полярную систему координат.
, для удобства вычислений перейдём в полярную систему координат.
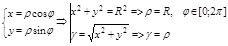
3. 
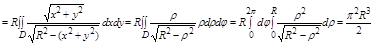
4. Поток жидкости через поверхность. Поверхностный интеграл II рода.
Рассмотрим установившееся течение жидкости в пространстве через данную точку 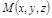 , когда скорость частиц жидкости зависит только от координат точки и не зависит от времени. В каждой точке
, когда скорость частиц жидкости зависит только от координат точки и не зависит от времени. В каждой точке 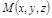 рассматриваемой пространственной области V задан вектор скорости частицы жидкости в этой точке
рассматриваемой пространственной области V задан вектор скорости частицы жидкости в этой точке
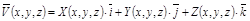 (3)
(3)
Плотность жидкости будем считать постоянной и равной единице.
Определение: Потоком жидкости через поверхность называется количество жидкости, свободно протекающее через неё за единицу времени.
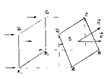 Пусть скорость течения жидкости одинакова во всех точках области и равна
Пусть скорость течения жидкости одинакова во всех точках области и равна 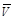 . Тогда поток жидкости П через прямоугольник
. Тогда поток жидкости П через прямоугольник 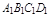 , расположенный в плоскости перпендикулярной вектору скорости
, расположенный в плоскости перпендикулярной вектору скорости 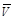 , будет равен
, будет равен
 .
.
Такое же количество жидкости протекает и через прямоугольник ABCD расположенный в плоскости, вектор нормали к которой 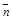 составляет с вектором скорости
составляет с вектором скорости 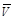 угол
угол  .
.
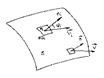 Пусть S – площадь фигуры ABCD, а значит
Пусть S – площадь фигуры ABCD, а значит 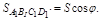 , тогда
, тогда
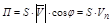 ,
,
где 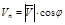 есть проекции вектора
есть проекции вектора 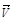 на нормаль
на нормаль 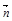 .
.
В общем случае в рассматриваемой пространственной области вектор скорости определяется соотношением (3). Найдем поток жидкости через поверхность S.
Для этого разобьем поверхность на n частей произвольным образом, площадь каждой части обозначим 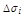 . На каждой площадке выберем произвольную точку
. На каждой площадке выберем произвольную точку  . Будем считать, что площадки
. Будем считать, что площадки 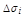 плоские, и в пределах каждой площадки скорость жидкости постоянна и равна скорости в точке
плоские, и в пределах каждой площадки скорость жидкости постоянна и равна скорости в точке  . Тогда приближенное выражение для потока жидкости через поверхность S имеет вид
. Тогда приближенное выражение для потока жидкости через поверхность S имеет вид
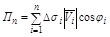 (4)
(4)
Заметим, что 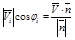 – есть проекция вектора скорости
– есть проекция вектора скорости 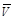 на направление
на направление 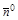 . Единичный вектор нормали задаётся направляющими косинусами углов, которые он образует с осями координат
. Единичный вектор нормали задаётся направляющими косинусами углов, которые он образует с осями координат
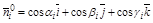
тогда с учетом (3) имеем
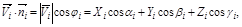
где

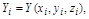

Переходя к пределу при 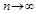 и при условии, что каждая площадка стягивается в точку, мы получим выражение для потока жидкости П:
и при условии, что каждая площадка стягивается в точку, мы получим выражение для потока жидкости П:
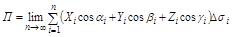
Определение: Предел интегральной суммы при 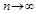 , если он существует и не зависит от способа разбиения поверхности S на части
, если он существует и не зависит от способа разбиения поверхности S на части  и от выбора точек
и от выбора точек 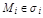 называется поверхностным интегралом второго рода и обозначается
называется поверхностным интегралом второго рода и обозначается


 (5)
(5)
Замечание: Если поверхность S замкнута, то поверхностный интеграл по её внешней стороне обозначается 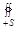 , а по внутренней
, а по внутренней  .
.
Свойства поверхностных интегралов II рода:
1. Поверхностных интегралов II рода зависит от направления нормали к поверхности. Обычно различают две стороны поверхности:
а) нормаль внешняя +S, для которого 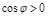 ;
;
б) нормаль внутренняя –S, для которого 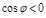 ;
;
Тем самым интеграл изменяет знак при перемене стороны поверхности.

2. Постоянный множитель можно выносить за знак интеграла.
3. Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
4. Поверхностный интеграл обладает свойством аддитивности, т.е. если 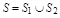 то
то

5. Если 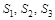 цилиндрические поверхности с образующими, параллельными соответственно осям Ox, Oy, Oz, то
цилиндрические поверхности с образующими, параллельными соответственно осям Ox, Oy, Oz, то
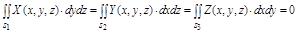
5. Вычисление поверхностных интегралов II рода.
Метод проекции на все три координатных плоскости.
 Интегралы (5) удобно вычислять как сумму трех интегралов. Начнем с последнего слагаемого
Интегралы (5) удобно вычислять как сумму трех интегралов. Начнем с последнего слагаемого
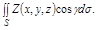
Пусть поверхность S задана уравнение  .
.
Возьмем элемент dxdy области  – проекции поверхности на плоскость Oxy и элемент
– проекции поверхности на плоскость Oxy и элемент  поверхности S проектирующийся в элемент dxdy. Нормаль
поверхности S проектирующийся в элемент dxdy. Нормаль 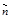 к площадке
к площадке 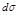 образует острый угол
образует острый угол 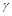 с положительным направлением оси Oz. Будем считать, что в пределах площадки, направление нормали
с положительным направлением оси Oz. Будем считать, что в пределах площадки, направление нормали 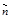 не меняется, т.е.
не меняется, т.е. 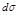 рассматривается как часть плоскости, касательной поверхности S в точке M. Тогда в силу
рассматривается как часть плоскости, касательной поверхности S в точке M. Тогда в силу 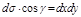 получим
получим
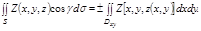
Знак 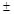 определяется знаком направляющего косинуса в силу двусторонности поверхности S.
определяется знаком направляющего косинуса в силу двусторонности поверхности S.