Задания на лабораторную работу №4
«Программирование численных методов»
Составить отчет, в котором содержится задание, листинг программы, числовые и графические результаты расчета. Поиск значения функции в методах нахождения интеграла и корней оформить в виде m-функции, сам метод в виде m-сценария. Построить график функции.
| № | Задание | ||
| 1. | Найти корень уравнения f(x)=0,25x3+x-1,25=0 на интервале [-2;2], используя метод деления пополам. Процесс вычисления корня закончить при выполнении условия 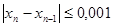 . .
| ||
| 2. | По формуле правых прямоугольников с шагом h=0,2 вычислить интеграл
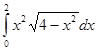 . .
| ||
| 3. | Решить с точностью 0,001 методом деления пополам нелинейное уравнение 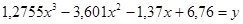 на интервале [-2,2]. на интервале [-2,2].
| ||
| 4. | По формуле левых прямоугольников с шагом h=0,01 вычислить интеграл

| ||
| 5. | Найти корень уравнения 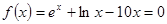 на интервале [3;4], используя метод деления пополам. Процесс вычисления корня закончить при выполнении условия на интервале [3;4], используя метод деления пополам. Процесс вычисления корня закончить при выполнении условия 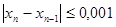 . .
| ||
| 6. | По формуле правых прямоугольников с шагом h=0,2 вычислить интеграл
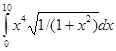 . .
| ||
| 7. | Решить с точностью 0,001 на интервале [0;1] методом деления пополам нелинейное уравнение  . .
| ||
| 8. | Решить с точностью 0,001 методом последовательных деления пополам нелинейное уравнение  на интервале [1; 5]. на интервале [1; 5].
| ||
| 9. | По формуле трапеций с шагом h=0,1 вычислить интеграл  . .
| ||
| 10. | Найти корень уравнения f(x)=5x4+2x-10=0 на интервале [-10;10], используя метод деления пополам. Процесс вычисления корня закончить при выполнении условия 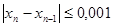 . .
| ||
| 11. | По формуле левых прямоугольников с шагом h=0,1 вычислить интеграл

| ||
Теоретические сведения
Метод левых прямоугольников (трапеций)
Геометрический смысл интеграла – площадь, которую ограничивает функция и ось 0Х. Метод заключается в разбиении этой площади на элементарные прямоугольники.
Отрезок 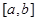 разбивается на
разбивается на  равных частей:
равных частей: 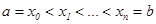 , где
, где 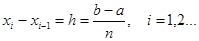
 . На участках
. На участках  , функцию
, функцию  для метода левых прямоугольников заменяют на отрезок, проходящий через левую точку функции параллельный оси 0X (см. рисунок).
для метода левых прямоугольников заменяют на отрезок, проходящий через левую точку функции параллельный оси 0X (см. рисунок).

Рисунок 1 – Графическая интерпретация метода левых прямоугольников
Численному значению интеграла полученной функции на участке  будет соответствовать сумма площадей полученных прямоугольников
будет соответствовать сумма площадей полученных прямоугольников
Метод деления отрезка пополам для решения уравнений
В функциях приводимых в задании предполагается, что они обладают непрерывными производными, кроме того, отделен корень уравнения - это значит найден такой интервал (a, b), который, во-первых, содержит корень уравнения и, во-вторых, содержит только один корень этого уравнения. Доказывается, что если на концах некоторого интервала (a, b) функция имеет разные знаки, а внутри этого интервала производная знак не меняет, то в интервале (a, b) корень уравнения есть и, при том, только один.
Отсюда возникает простая методика приближенного поиска корня, отделенного в интервале (a, b): надо построить последовательность точек по следующему правилу:
1. Вычисляется функция в точках a, b, (a+b)/2;
2. Определяется тот из двух интервалов [a, (a+b)/2] и [(a+b)/2, b] на концах которого функция имеет разные знаки (т.е. функция пересекает ось);
3. Передвигаем границу, со стороны которой от середины не имеет корня в середину (a=(a+b)/2 или b=(a+b)/2 в зависимости от предыдущего шага);
4. Итерацию повторяют до достижения некоторой точности вычислений 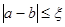 . Последнее значения границ перед прерыванием построения последовательности и принимается за приближенное с заданной степенью точности значение корня.
. Последнее значения границ перед прерыванием построения последовательности и принимается за приближенное с заданной степенью точности значение корня.