Лабораторное занятие 2.
КИНЕТИКА БИОЛОГИЧЕСКИХ ПРОЦЕССОВ.
Теоретическая часть
Все биологические процессы протекают во времени. Для описания и оценивания этого удобной количественной характеристикой является скорость реакции или скорость процесса. Знание механизмов реакций и процессов, обеспечивающих их протекание с той или иной скоростью, зависимость скорости от различных факторов (концентрации веществ, температуры, рН, наличия катализаторов-ферментов, активаторов, ингибиторов и т.д.) позволяет прогнозировать развитие реакций или процессов, оптимизировать их протекание в нужном направлении и с необходимым результатом.
Представим химическое превращение в виде простой реакции:
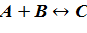
Скоростью этой химической реакции будет величина накопления продукта в единицу времени
;
Кинетика базируется на фундаментальном положении Гулдберга-Вааге, согласно которому скорость реакции пропорциональна произведению концентраций реагирующих веществ в степенях, соответствующих их стехиометрическим коэффициентам. Это положение, связывающее активные концентрации веществ со скоростью реакции, так же известно как закон действующих масс. В соответствие с этим законом скорость реакции может быть выражена в следующем виде:
где к – коэффициент пропорциональности, называемый константа скорости реакции.
Рассмотрим вариант простейшей реакции 1 -го порядка, когда Скорость реакции в этом случае можно выразить как 
Знак минус на расходование реагента в ходе реакции.
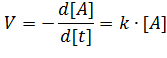
Пусть в начальный момент времени t=0 концентрация вещества А равна [А]0. После начала реакции начнется постепенное расходование реагента А и к моменту времени t = t его концентрация станет [А]. Используя эти граничные условия, проинтегрируем уравнение скоростей, предварительно разделим переменные
;
; 
;
Отсюда или 
или 
;
Из этого уравнения после потенцирования выражение для зависимости| изменения концентрации вещества от времени 
При переходе к десятичным логарифмам получается 
;
Отсюда определяется константа скорости 
, где [А]0 и [А] - начальная и конечная концентрации вещества А.
Помимо зависимости от концентрации реагентов скорость реакции существенно зависит от температуры. Известно эмпирическое правило, называемое законом Вант-Гоффа, согласно которому при повышении температуры на 10° скорость реакции возрастает приблизительно в 2 раза. Отношение констант скоростей реакции при двух температурах, различающихся на 10°, называется температурным коэффициентом 
.
Правило Вант-Гоффа приближенное, поскольку температурный коэффициент Q10 меняется с температурой. Более точная зависимости скорости реакции (константы скорости) от температуры выражается уравнением Аррениуса, которое учитывает кинетическую энергию реагентов, определяющих характер влияния на скорость реакции: 
, где А — предэкспоненциальный множитель, Т — абсолютная температура (К), R — универсальная газовая постоянная (1.98•10-3 ккал/М•градус), Еа - энергия активации. Она характеризует величиной энергетического потенциального барьера, который молекулы реагентов должны преодолеть для взаимодействия.
Для любого температурного интервала Q10 вычисляется по формуле Вант-Гоффа: 
, где К1 и К2 константы скорости реакции при температурах t1 и t2 соответственно.
Очевидно при t2 = t1 + 10, 
; 
(пpи 
)
При изучении биологических процессов вычисление К обычно затруднительно и ее заменяют непосредственно величиной скорость процесса. Энергия активации, т.е. температурная характеристика процесса выводится из уравнения Аррениуса для скорости химической реакции:
, где Ea - энергия активации.
Из уравнения следует: 
.
Формула устанавливает простое соотношение между Еа и Q10. Действительно, при T2-T1=10 и при переходе от ln к lg путем умножения на модуль 2,3 имеем: 
[кал/град•моль].
Энергия активации связана с температурным коэффициентом эмпирическим соотношением: 
Прологарифмировав интегральное уравнение Аррениуса, получим выражение, удобное для определения величины энергии активации из экспериментально полученных величин: 
Из этого выражения следует, что 
(или 
) линейно зависит от величины обратной температуры (1/Т) (рис.1.1). Это очень удобно для графического представления кинетических экспериментальных данных. Если по оси ординат откладывать значения (или ), а по оси абсцисс -1/Т (координаты Аррениуса), то из наклона этого графика легко определяется величина энергии активации Еа.
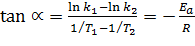отсюда 
;
Рис. 1.1. Диаграмма Аррениуса (представление экспериментальных данных в координатах Аррениуса).
Наиболее точно зависимость константы скорости реакции от температуры определяется на основе теории абсолютных скоростей реакций Эйринга. Эта зависимость выражается уравнением Эйринга:
, где к0 - постоянная Больцмана 1.88*10-23 Дж/К; h - постоянная Планка 6.625*10-34 Дж*сек; 
— изменение энтропии и энтальпии соответственно в результате химического превращения или процесса.
| Рис. 1.2. Примерный вид зависимости ЧСС от температуры. |
Экспериментальная часть
Материалы и оборудование: лягушки, наборы препаровальных инструментов, препаровальные ванночки, 10% раствор этилового спирта для анестезии, раствор Рингера для холоднокровных, гигроскопическая вата, секундомер, стеклянные термостаты, лабораторные термометры.
Методика выполнения работы.
Работа может выполняться в двух вариантах: а) на изолированном сердце по Штраубу (если есть крупные лягушки); б) если животные мелкие, то эксперимент проводится на целой лягушке с открытым сердцем.
При реализации варианта а) необходимо тщательно отпрепарировать сердце лягушки (рис.1.3). Для этого животное после лёгкой анестезии (помещение в сосуд с 10% раствором этилового спирта на 15 минут) обездвиживается (кровным или бескровным методом путём разрушения спинного и головного мозга) и фиксируется в препаровальной ванночке. Приподняв пинцетом кожу на брюшке, делаются разрезы под пинцетом по направлению к обеим ключицам, отгибается лоскут кожи и отрезается. Далее под грудной костью делается прорез, в него вводится бранша ножниц и производится осторожное прорезание мышц по обе стороны грудной кости, после чего кость отстригается и открывается сокращающееся сердце. Далее сердце изолируется с некоторым количеством прилегающих тканей.
Отпрепарированное сердце помещается в физиологический раствор при комнатной температуре. Через 5 минут производится оценка частоты сокращений, чтобы оценить исходное функциональное состояния органа. После этого препарат фиксируется на канюле с физиологическим раствором и переносится во влажную камеру-термостат, в котором опускается в снег для понижения температуры до 2-5 градусов.
При выполнении работы по варианту б) животное после анестезии обездвиживается бескровным путём и проводится описанная выше процедура вскрытия грудины и обнажения сокращающего сердца (рис. 1.4). Далее разрез закрывается ватой, обильно смоченной раствором Рингера при комнатной температуре, животное фиксируется в стакане-термостате и начинается охлаждение препарата сердца до необходимой температуры.
| Рис. 1.3. Схема установки для измерения Q10 и Еа сокращений сердца лягушки. 1 - изолированной сердце лягушки по Штраубу; 2 - термометр; 3 -термостат (сосуд со льдом или водой t°=2-5 °C); А — широкая пробирка. |
| Рис. 1.4. Вид вскрытой грудины лягушки с открытым сердцем для подсчёта частоты сердечных сокращений при различных температурах. | 
|
Задание №l. Определение энергии активации сокращений сердца лягушки по величине Q10
Для выполнения работы необходимо определить скорость сокращений (ЧСС) при нескольких значениях температур (не менее 3), отличающихся на 10 градусов. ЧСС для каждого температурного режима определяется не менее 3 раз. Далее по средним значениям ЧСС определяется коэффициент Вант-Гоффа, по которому рассчитывается кажущаяся энергия активации исследуемого процесса по формуле 
[кал / град. моль].
Задание №2. Определение энергии активации сокращений сердца лягушки с помощью графика Аррениуса.
Для выполнения задания необходимо полученные значения скоростей сокращения сердца прологарифмировать и построить график зависимости полученных значений от обратной температуры (график в координатах Аррениуса). По тангенсу угла наклона графика определить значения Еа в каждом температурном диапазоне.