Рассмотрим идею БПФ с прореживанием по времени (decimation in time, DIT) на примере деления набора отсчетов пополам.
Итак, пусть N — четное число. Выделим в формуле ДПФ два слагаемых, соответствующих элементам исходной последовательности с четными и нечетными номерами:
Введем обозначения y(m) = x(2m) и z(m) = x(2m + 1), а также вынесем из второй суммы общий множитель e− π j2 n /N:
Две суммы выше, представляют собой ДПФ последовательностей {y(m)} (отсчеты с четными номерами) и {z(m)} (отсчеты с нечетными номерами). Каждое из этих ДПФ имеет размерность N/2. Таким образом,
где Y(n) и Z(n) — ДПФ, соответственно, последовательностей отсчетов с четными и нечетными номерами:
Так как ДПФ размерности N/2 дает лишь N/2 спектральных коэффициентов, непосредственно использовать формулу можно только при 0 ≤ n < N/2. Для остальных n (N/2 ≤ n < N) следует воспользоваться периодичностью спектра дискретного сигнала (и, соответственно, периодичностью результатов ДПФ):
(*)
С учетом этого при n ≥ N/2 формула ДПФ представляется в виде
(**)
Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных ДПФ иллюстрируется на рисунке.
Блоки, выполняющие на рис. 5.3 объединение результатов двух ДПФ, требуют дополнительных комментариев. Каждый такой блок имеет два входных и два выходных сигнала. Один из входных сигналов умножается на комплексную экспоненту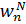 
, после чего суммируется со вторым входным сигналом и вычитается из него, формируя таким образом два выходных сигнала. Это соответствует реализации
формул (*) и (**). Данная операция получила название "бабочки" (butterfly).
Оценим количество операций, необходимое для вычисления ДПФ указанным способом. Каждое из двух ДПФ половинной размерности требует N 2 /4 операций.
Кроме того, при вычислении окончательных результатов каждый спектральный коэффициент Z(n) умножается на экспоненциальный комплексный множитель.
Это добавляет еще N/2 операций. Итого получается 
, что почти вдвое меньше, чем при вычислении ДПФ прямым способом.
Если N/2 тоже является четным числом (т. е. если N делится на 4), можно продолжить описанную процедуру, выразив результат через четыре ДПФ размерности N/4.
Это позволяет еще больше сократить число требуемых вычислительных операций.
Наибольшая степень ускорения вычислений может быть достигнута при N = 2k, в этом случае деление последовательностей на две части можно продолжать до тех пор, пока не получатся двухэлементные последовательности, ДПФ которых рассчитывается вообще без использования операций умножения (достаточно вычислить сумму и разность двух отсчетов).
Оценим количество арифметических операций для случая N = 2k. Выделим в приведенной структуре отдельные каскады преобразования. Размерность ДПФ в смежных каскадах отличается в два раза, поэтому общее число каскадов составляет Log2 (N) (самый первый каскад осуществляет только перестановку отсчетов и не требует арифметических операций). Каждый каскад содержит N/2 "бабочек", для реализации каждой "бабочки" необходимо два комплексных сложения и одно комплексное умножение. Считая затраты на одну "бабочку" равными двум парам комплексных операций "умножение-сложение", получаем общее
число таких операций, равное 
Таким образом, вычислительные затраты по сравнению с непосредственным использованием формулы ДПФ уменьшаются в N/log2(N) раз. При больших N это отношение становится весьма велико (например, при N = 1024 достигается более чем стократное ускорение).