Лекция 1.
Задача о наилучшем приближении.
Задача о наилучшем приближении в Rn.
Поставим задачу – приблизить наилучшим образом вектор трехмерного пространства вектором v в двухмерном пространстве - плоскости.
Ясно, что интуитивно наилучший выбор v – ортогональная проекция вектора u на эту плоскость. Пусть e1 , e2 – ортогональные базисные векторы, а плоскость – их линейная оболочка, тогда v = C1 e1 + C2 e2. Остается найти коэффициенты разложения C1, C2.
Если v – ортогональная проекция вектора u на плоскость, то вектор u – v ортогонален плоскости, следовательно, ортогонален и базисным векторам. Тогда
0 = (u --v, e1) =([u – ( C1 e1 + C2 e2)], e1) = (u, e1) – C1 (e1, e1), 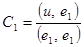
0 = (u --v, e2) =([u – ( C1 e1 + C2 e2)], e2) = (u, e2) – C2 (e2, e2), 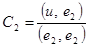 .
.
Здесь (e1, e2) = 0, так как базисные векторы ортогональны.
Аналогично решается задача наилучшего приближения вектора из Rn+1 вектором из Rn: Наилучший выбор приближения – проекция вектора на Rn.
V = C1 e1 +… Cn en, где 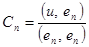 .
.
Задача о наилучшем приближении в Н (гильбертовом пространстве).
Скалярное произведение. Численнозначная функция двух элементов (f,g) называется скалярным произведением, если выполнено
1) (f, f) 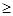 0, (f, f) = 0
0, (f, f) = 0 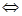 f =0
f =0
2) (f, g) = (g, f)
3) (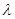 f, g) =
f, g) = 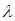 (f, g) = (f,
(f, g) = (f, 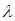 g)
g)
4) (f + g, h) = (f, h) + (g, h)
Заметим, что здесь 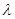 считается действительным числом. Если считать
считается действительным числом. Если считать 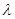 комплексным числом, то третье свойство надо определять так: (
комплексным числом, то третье свойство надо определять так: (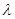 f,g) =
f,g) = 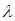 (f,g), (f,
(f,g), (f, 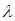 g), =
g), = 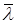 (f, g), где
(f, g), где 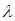 и
и 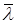 - комплексно-сопряженные числа.
- комплексно-сопряженные числа.
Упражнение. Покажите, что
1) (a, b) = |a| |b| cos 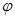 - скалярное произведение векторов a, b,
- скалярное произведение векторов a, b,
2) ((x1 … xn), (y1, … yn)) = (x1 y1 + … + xn yn) – скалярное произведение векторов – строк,
3) (f(x), g(x)) = 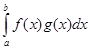 - скалярное произведение функций
- скалярное произведение функций 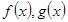 , заданных на отрезке
, заданных на отрезке 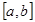 .
.
Если в пространстве задано скалярное произведение, то, задавая норму в пространстве соотношением 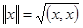 , можно сделать пространство нормированным.
, можно сделать пространство нормированным.
Задавая метрику соотношением 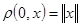 , можно сделать нормированное пространство метрическим.
, можно сделать нормированное пространство метрическим.
Если в пространстве задано скалярное произведение, то в нем можно определить углы и расстояния между элементами 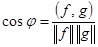 .
.
Гильбертовым пространством H называется полное, бесконечномерное, сепарабельное линейное пространство со скалярным произведением.
Пространство полно, если любая фундаментальная последовательность его элементов сходится к элементу пространства.
Пространство сепарабельно, если в нем существует счетное всюду плотное множество (как рациональные числа среди действительных чисел).
Элементы (функции) гильбертова пространства называются векторами (бесконечномерные векторы над осью действительных чисел, так как функция полностью определяется всеми своими значениями (при всех значениях аргумента, а их бесконечное число)).
Функции ортогональны, если (f, g) = 0.
Система функций называется полной, если любой элемент пространства может быть разложен по этой системе (представлен в виде линейной комбинации ее элементов).
Можно показать, что любая система из бесконечного количества попарно ортогональных функций полна в гильбертовом пространстве.
Мы будем считать, что функции 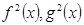 интегрируемы на отрезке
интегрируемы на отрезке 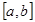 , и рассматривать гильбертово пространство L2 со скалярным произведением (f(x), g(x)) =
, и рассматривать гильбертово пространство L2 со скалярным произведением (f(x), g(x)) = 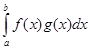 над полем действительных чисел. Введем в нем норму элемента:
над полем действительных чисел. Введем в нем норму элемента:
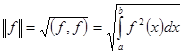 . Назовем среднеквадратическим уклонением функции
. Назовем среднеквадратическим уклонением функции 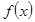 от функции
от функции 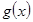 величину
величину 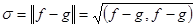 .
.
Рассмотрим задачу о наилучшем приближении в пространстве L2 функции 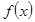 линейной комбинацией конечного числа ортогональных функций
линейной комбинацией конечного числа ортогональных функций 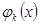 .
.
Выбрать действительные коэффициенты 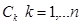
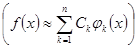 ,
, 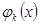 - попарно ортогональны, чтобы минимизировать среднеквадратическое уклонение функции от линейной комбинации
- попарно ортогональны, чтобы минимизировать среднеквадратическое уклонение функции от линейной комбинации
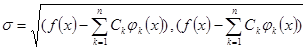 .
.
Преобразуем выражение для 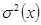 , применяя известную еще из школы процедуру выделения полного квадрата и учитывая ортогональность функций
, применяя известную еще из школы процедуру выделения полного квадрата и учитывая ортогональность функций 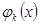 : (
: (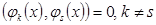 ).
).
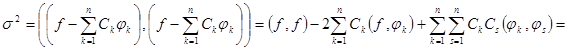
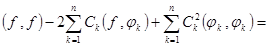
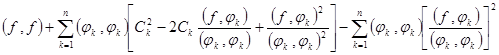 =
=
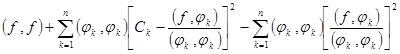 .
.
Минимизировать это выражение по 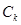 - означает минимизировать второе слагаемое, в котором содержатся коэффициенты
- означает минимизировать второе слагаемое, в котором содержатся коэффициенты 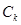 . Это слагаемое неотрицательно, так как
. Это слагаемое неотрицательно, так как 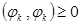 (свойство скалярного произведения), а квадратная скобка, в которую входят
(свойство скалярного произведения), а квадратная скобка, в которую входят 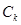 , стоит в квадрате. Следовательно, минимизировать это второе слагаемое – означает сделать его нулевым, выбрав коэффициенты
, стоит в квадрате. Следовательно, минимизировать это второе слагаемое – означает сделать его нулевым, выбрав коэффициенты
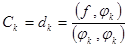 . Коэффициенты
. Коэффициенты 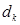 называются коэффициентами Фурье.
называются коэффициентами Фурье.
Если 
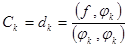 , то
, то 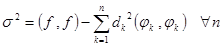 . Но
. Но 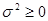 , поэтому
, поэтому
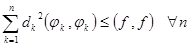 или
или 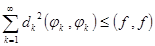 . Эти неравенства называются неравенствами Бесселя.
. Эти неравенства называются неравенствами Бесселя.
Если система функций 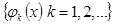 полна (в гильбертовом пространстве это выполнено, так как функции попарно ортогональны), то справедливо равенство Парсеваля
полна (в гильбертовом пространстве это выполнено, так как функции попарно ортогональны), то справедливо равенство Парсеваля 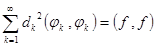 .
.
В самом деле, пусть 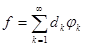 . Тогда
. Тогда 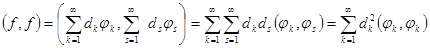 (так как
(так как 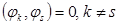 ).
).
Если функции 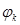 не только ортогональны, но еще и ортонормированны, т.е.
не только ортогональны, но еще и ортонормированны, т.е. 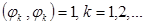 , то равенство Парсеваля – это аналог теоремы Пифагора в бесконечномерном пространстве
, то равенство Парсеваля – это аналог теоремы Пифагора в бесконечномерном пространстве 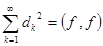 .
.
Следствие из равенства Парсеваля. Пусть выполнено равенство Парсеваля, пусть 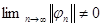 . Тогда
. Тогда 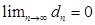 .
.
Доказательство. Пусть выполнено равенство Парсеваля 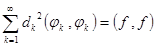 . Тогда по необходимому признаку сходимости ряда
. Тогда по необходимому признаку сходимости ряда 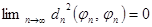 . Так как
. Так как 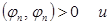
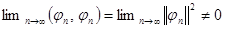 , тогда
, тогда 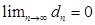 .
.