Лабораторная работа №2. Приближение значения таблично заданной функции в точке с помощью интерполяционных многочленов

ПАКЕТЫПРИКЛАДНЫХ ПРОГРАММ В УПРАВЛЕНИИ

Методические указания

Волгоград

УДК: 681.5

Рецензенты:

канд. техн. наук доц. ВПИ (филиал) ВолгГТУ Л.И. Медведева

Издается по решению редакционно-издательского совета

Волгоградского государственного технического университета

Силаев А.А.,

Пакеты прикладных программ в управлении: методические указания /А. А. Силаев, Е.Ю. Силаева; ВПИ (филиал)ВолгГТУ. – Волгоград: Изд-во ВолгГТУ, 2017. – 22 с.

В методических указаниях рассмотрен порядок выполнения лабораторных работ по дисциплине «Пакеты прикладных программ в управлении» на тему применение числовых методов для решения дифференциальных уравнений и интерполяции функций.

Предназначены для студентов технических ВУЗов обучающихся по направлению бакалавриата «Автоматизация технологических процессов и производств» всех форм обучения.

Ó Волгоградский государственный технический университет, 2017 Ó Волжский политехнический институт, 2017

Содержание

Лабораторная работа №1. Решение обыкновенных дифференциальных уравнений. 4

Метод Эйлера и модификации. 6

Метод Рунге–Кутта. 9

Задание для индивидуального выполнения: 12

Лабораторная работа №2. Приближение значения таблично заданной функции в точке с помощью интерполяционных многочленов. 13

Интерполяционный полином Лагранжа. 13

Интерполирование сплайнами. 15

Задание для индивидуального выполнения: 18

Список литературы.. 21

Лабораторная работа №1. Решение обыкновенных дифференциальных уравнений.

Цель работы: научиться решать задачи Коши для дифференциальных уравнений на отрезке [а, b] при заданном начальном условии методами Пика, Эйлера, Рунге–Кутта.

Исходные данные:

Решить задачу Коши для дифференциального уравнения на отрезке [1,7; 2,7] при заданном и шаге интегрирования h=0,1 методом Пика с шагом h.

Решение:

1. Введем данные:

2. Задаем функцию, возвращающую значения первой производной по переменной y:

3. Составим функцию, возвращающую решение дифференциального уравнения методом Пика. Рассмотрим функции f – исходная функция; f_deriv – производная функции по y; a, b – концы отрезка; h – шаг; y0 – начальное значение переменной y.

4. Нахождение численного решения дифференциального уравнения методом Пика

Метод Эйлера и модификации

Решить задачу Коши для дифференциального уравнения на отрезке [1,7; 2,7] при заданном и шаге интегрирования h=0,1 методом Эйлера h и h/2.

Решение:

1. Введем данные:

2. Решение методом Эйлера:

3. Составим программу реализующая метод Эйлера:

4. Получим решение методом Эйлера:

Метод Рунге–Кутта

Решить задачу Коши для дифференциального уравнения на отрезке [1,7; 2,7] при заданном и шаге интегрирования h=0,1 методом Пика с шагом 2h.

Решение:

1. Введем данные:

2. Составим функцию, возвращающую решение дифференциального уравнения первого порядка методом Рунге–Кутта. Рассмотрим функции fn – исходная функция; a, b – концы отрезка; h – шаг; y0 – начальное значение переменной y.

3. Найдем решение дифференциального уравнения первого порядка, использую встроенные функции Mathcad:

Задание для индивидуального выполнения:

	№	f(x, y)	[a, b]	y0	h
Буланов	1.		0,2; 1,2	y(0,2)	0,1
Вакуленко	2.		1,6; 2,6	y(1,6)=4,6	0,1
Воронов	3.		0,2; 1,2	y(0,2)=1,1	0,1
Вылегжанин	4.		1,4; 2,4	y(1,4)=2,5	0,1
Голованов	5.		1,7; 2,7	y(1,7)=5,3	0,1
Гурнутин	6.		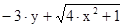2,6; 4,6	y(2,6)=3,5	0,2
Ибрагимов	7.		2; 3	y(2)=2,3	0,1
Исенгалиев	8.		0; 1	y(0)=0,3	0,1
Кожевников	9.		1,8; 2,8	y(1,8)=2,6	0,1
Конистратенко	10.		0,2; 1,2	y(0,2)	0,01
Коркин	11.		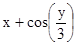1,6; 2,6	y(1,6)=4,6	0,2
Лашманов	12.		0,2; 1,2	y(0,2)=1,1	0,05
Лебедев	13.		1,4; 2,4	y(1,4)=2,5	0,02
Лёвочкин	14.		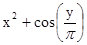1,7; 2,7	y(1,7)=5,3	0,15
Матюшанов	15.		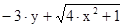2,6; 4,6	y(2,6)=3,5	0,02
Мельничук	16.		2; 3	y(2)=2,3	0,01
Николаев	17.		0; 1	y(0)=0,3	0,02
Носенко	18.		1,8; 2,8	y(1,8)=2,6	0,01
Носиков	19.		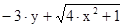2,6; 4,5	y(2,6)=3,5	0,02
Овчинников	20.		1,4; 2,4	y(1,7)=5,3	0,15
Татьянко	21.		0,2; 1,5	y(0,2)	0,01
Чурсин	22.		0,4; 1,4	y(0,2)=1,1	0,05