Способы представления графов

РАЗДЕЛ 2 ТЕОРИЯ ГРАФОВ

 

Лекция Введение в теорию графов

 

Основные понятия и определения.

2. Способы представления графов.

 

Основные понятия и определения

Граф можно рассматривать, как набор точек, называемых вершинами, соединенных между собой линиями, называемыми ветвями. Представление ряда физических систем в виде графа является совершенно естественным, в то время как в других случаях связь между самой системой и её моделью в виде графа может быть довольно сложной. К первой группе относятся, например, системы связи, информационно-вычислительные сети и транспортные системы. Ветви графа могут соответствовать линиям связи, каналам передачи данных, железным дорогам, автомобильным дорогам, авиалиниям и т.п. Вершины графа могут представлять узлы связи, терминалы, компьютеры, коммутаторы, телефонные станции, телефонные аппараты и т.п., то есть точки, в которых информационные потоки возникают, задерживаются и оканчиваются.

Структурно сходные физические сети могут иметь различные характеристики. Например, как электрическая, так и телефонная сети могут быть представлены в виде графа. Однако в первом случае ветви характеризуются такими параметрами, как сопротивление, индуктивность, емкость, в то время как ветви модели телефонной сети характеризуются максимальной пропускной способностью и стоимостью разговора.

Определим основные понятия, которыми будем манипулировать в дальнейшем.

Прежде всего введём понятия неупорядоченной и упорядоченной пар.

Если x и y какие-либо элементы, то из них можно образовать двухэлементное множество {x,y} (или, что то же самое {y,x}), которое в дальнейшем называется неупорядоченной парой элементов x,y и часто обозначается в квадратных скобках [x,y]. Из этих же элементов можно образовать ещё два новых объекта:

1.Упорядоченную пару с первой компонентой x и второй компонентой y, которая обозначается (x,y).

2. Упорядоченную пару с первой компонентой y и второй компонентой x, которая обозначается (y,x).

Если x¹y, то упорядоченные пары (x,y) и (y,x) считаются различными.

Приведём теперь определение графа.

Конечный граф G=(V,E) это совокупность множества V={v₁,v₂,…,v_n}, элементы которого называются вершинами (узлами, точками), и множества E={e₁,e₂,…,e_m}, элементы которого называются рёбрами (ветвями). Каждому ребру e соответствует пара вершин v_i,v_j из V.

Говорят, что ребро e соединяет вершину v_i с вершиной v_j, или ребро e инцидентно вершинам v_i и v_j.

Ребро называется ориентированным или дугой, если пара вершин v_i,v_j, соответствующая этому ребру e упорядочена. Вершину v_i называют начальной вершиной, а v_j - конечной вершиной дуги е. Граф содержащий только ориентированные ребра называется ориентированным или орграфом. Граф, содержащий как ориентированные, так и неориентированные ребра называют смешанным.

Обычно конечный граф представляется диаграммой, и её часто называют графом. При построении диаграммы каждой вершине vÎV ставится в соответствие окружность (точка) на плоскости. Если вершины v_i,v_j соединены в граф ребром, то окружности (точки) отмеченные как, v_i и v_j соединяются отрезком линии. Ориентация дуг на диаграмме отмечается стрелкой, направленной из начальной вершины дуги в конечную. Форма и длина соединяющих линий на диаграмме может быть произвольной; они могут пересекаться. Диаграммы неориентированного и ориентированного графов изображены соответственно на рис. 2.1 и 2.2.

 

v4

v2

e9

e8

e10

e3 bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbl3

e5

e2

e1

e4

e6

v3

v6

v5

v1

e7

Рисунок 2.1 – Неориентированный граф

 

Приведённое определение графа не запрещает соединять две вершины несколькими рёбрами или дугой. Говорят, что два ребра (дуги) кратны или параллельны, если они имеют одну и туже пару концевых вершин (для дуг дополнительно требуется одинаковая ориентация). Например в графе, изображённом на рисунке 2.1 ребра e₁ и e₂ являются кратными. В орграфе, изображенном на рисунке 2.2, дуги e₁ и e₂ кратны, а дуги e₃ и e₄ кратными не являются, т. к. их направления не совпадают. Кратные ребра могут быть обозначены упорядоченными парами соответствующих вершин с различными индексами.

Например, для графа изображенного на рис.2.2 дугу e₁ можно обозначить (v₁,v₂) ₁, а дугу e₂ -через (v₁,v₂) ₂.

Дуга орграфа называется петлёй, если она начинается и кончается в одной и той же вершине (e₉ - петля <=> e₉=(v₅,v₅)). Петли в неориентированных графах определяются аналогично.

V4

e1

e2

e3

e4

e6

e5

e7

e8

e9

V1

V2

V5

V3

Рисунок 2.2 – Ориентированный граф

 

Граф, который не содержит кратных ребер (дуг) и петель, называется простым. Такой граф изображён на рис. 2.3.

V5

V2

V1

V3

V4

Рисунок 2.3 – Простой граф

 

Подграфом графа G называется граф, у которого все вершины и ребра (дуги) принадлежат G. Остовный подграф - это подграф графа G, содержащий все его вершины. Говорят,что подграф G^’=(S,N ) графа G=(V,E ) индуцирован (порождён) подмножеством вершин SÌV, если он получен в результате удаления вершин V\S и всех ребёр (дуг), инцидентных им.

Граф называется планарным, если он может быть изображён на плоскости таким образом, что его рёбра (дуги) будут пересекаться только в вершинах. Граф, представленный на рисунке 2.3, не планарен. Изобразить его на плоскости без пересечения дуг невозможно.

Две вершины графа G называются смежными если существует по крайне мере одно соединяющее их ребро. Аналогично два ребра являются смежными, если существует инцидентная им вершина.

Степенью (валентностью) вершины v ( обозначение: r(v)) называется число инцидентных ей ребёр или дуг. Полустепенью захода вершины v (обозначение: r⁺(v)) называется число дуг, имеющих вершину v в качестве конечной. Полустепенью исхода вершины r ^--(v), называется число дуг, «выходящих» из v. Вершина степени 1 называется висячей, вершина степени 0 - изолированной.

Сеть G=(V,E,f) определяется как граф или орграф, рассматриваемый вместе с функцией f, приписывающей каждому ребру eÎE некоторое число (вес) f(e). В информационно-вычислительных сетях или транспортных сетях эти веса представляют некоторые физические величины, такие как расстояние между пунктами стоимость проезда, скорость передачи информации, надёжность канала передачи данных и т.п.

Маршруты и связность. Пусть G=(V,E) - неориентированный граф. Маршрутом в графе G называется такая чередующаяся последовательность вершин и ребер: 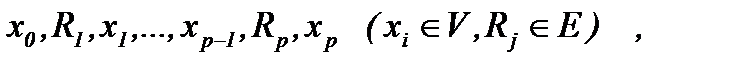что каждое ребро последовательности инцидентно двум вершинам, одна из которых непосредственно предшествует ему, а другая непосредственно следует за ним, т.е. R_j инцидентно x_j-1 и x_j. Указанный маршрут соединяет вершины x₀,x_p.

Вершина x₀ называется начальной, а x_p – конечной вершиной маршрута. Маршрут замкнут если x₀=x_p, и открыт в противном случае.. Маршрут называют цепью, если его ребра различны, простой цепью - если и вершины (а следовательно, и ребра) различны. Замкнутая цепь называется циклом.

Если все р вершин цикла различны и р>0, то он называется простым. Маршрут можно обозначить, указав последовательность его ребер. Если граф не содержит кратных ребер, маршрут может быть задан перечислением содержащихся в нем вершин в порядке их “прохождения”. Так, предыдущий маршрут может быть представлен в виде 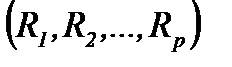или в виде (x₀,x₁,…,x_p). В графе изображенном на рисунке 2.4 (v₁,v₂,v₄,v₃,v₄,v₆) - маршрут, который не является цепью, а (v₁,v₂,v₄,v₃,v₂,v₅,v₆) - цепь, но не простая цепь, (v₁,v₂,v₅,v₆) - простая цепь, (v₂,v₃,v₅,v₂) - простой цикл.

V2

V4

V1

V3

V5

V6

 

Рисунок 2.4 – Неориентированный граф

 

Граф называется связным, если каждая пара его вершин может быть соединена (простой) цепью. Граф, который не является связным, может быть разбит на конечное число связных подграфов, называемых компонентами связности.

Длина маршрута определяется числом входящих в него ребер. Расстоянием d(x,y) между двумя вершинами x и y графа G называется длина соединяющей их кратчайшей простой цепи, а сама кратчайшая цепь называется геодезической; если x и y не соединены, то полагают . В связном графе расстояние является метрикой, т.е. удовлетворяет следующим аксиомам:

1) 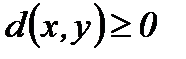и тогда и только тогда, когда x=y;

2) ;

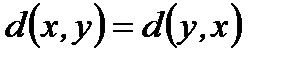3) .

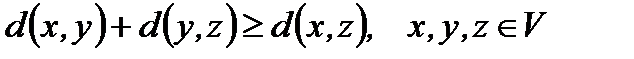Диаметром графа D(G) называется длина длиннейшей геодезической.

Множество вершин, находящихся на одном расстоянии n от вершины v называется ярусом D(v,n) = {uÎV | d(v,u)=n}.

Центром графа называется такая вершина (несколько вершин), что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа

Разрезом графа называется множество рёбер, удаление которых увеличивает число компонент. Разрез, не содержащийся ни в каком другом разрезе, называется простым. Так, в графе на рис.2.4 ребра, входящие в разрез, изображены тонкими линиями. Их удаление приводит к разбиению графа на две компоненты, выделенные жирными линиями.

Перейдём теперь к рассмотрению ориентированных графов.

Ориентированным маршрутом (ормаршрутом) в орграфе G=(V,U) называется последовательность вершин и дуг в которой каждая промежуточная вершина x_i является конечной для предшествующей дуги D_i и начальной для последующей дуги D_i+1.

Путь - это ориентированный маршрут, все дуги которого различны. Замкнутый путь 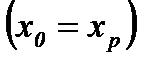называется контуром. Путь (контур) не содержащий повторяющихся вершин, называется простым путём (простым контуром).

 

V3

V4

V5

V2

V1

 

Рисунок 2.5 – Ориентированный граф

 

Например, в графе на рис. 2.5 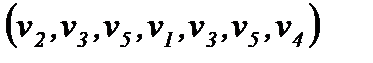- ориентированный маршрут, 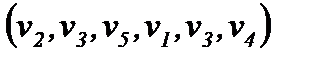путь из v₂ в v₄, 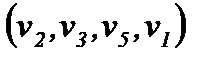- простой путь, и 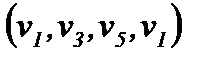- простой контур.

В орграфах можно также рассматривать неориентированные маршруты, цепи и циклы. В этом случае ориентация дуг не принимается во внимание. Двигаясь, например, вдоль цепи, можно пройти дугу в направлении, противоположном её ориентации. Дуги, проводимые в направлении ориентации, называются прямыми дугами цепи, а дуги, проводимые в направлении, противоположном ориентации, называются обратными.

Орграф называется связным, если для каждых двух вершин 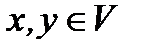существует соединяющая их цепь, и сильно связным, если существует путь от x к y и путь от y к x.

Деревья и обходы. Деревом в неориентированном графе G=(V,E) называется связный подграф, не имеющий циклов.

Если все вершины графа принадлежат дереву, то оно называется покрывающим деревом или остовом. Рёбра графа, принадлежащие покрывающему дереву, называются ветвями. Все остальные рёбра называются хордами. Например в графе, приведённом на рис.2.6, ветви покрывающего дерева изображены жирными линиями, а хорды тонкими.

V1

V2

V4

V6

V5

V3

 

Рисунок 2.6 – Неориентированный граф

 

Вершины дерева, для которых p(v)=1 называются концевыми или тупиковыми.

В дереве любые две вершины связаны единственной цепью. Это свойство деревьев является определяющим и широко используется в приложениях.

Ориентированным деревом (ордеревом) называется орграф без контуров, в котором для любой вершины v выполняется .

 

V5

V6

V1

V3

V2

V4

V7

 

Рисунок 2.7 – Ориентированное дерево

Вершина v, для которой 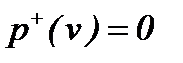, называется корнем дерева. В ордереве существует путь от v к каждой из других вершин. Вершины ордерева, для которых 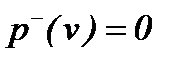, называются конечными вершинами или листьями. Граф, изображённый на рис.2.7, является ориентированным деревом; v₁ - корень дерева; 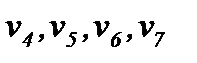- листья. Вершины одного уровня дерева называются ярусом.

Число различных деревьев, которые можно построить на m вершинах равно m^m-2. Много деревьев – это лес.

Цикломатическое число. Если граф имеет n вершин и m ребер, то цикломатическое число графа равно .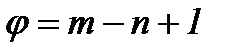

Цикломатическое число графа равно наибольшему количеству независимых (базисных) циклов.

Понятие независимых циклов наиболее просто можно трактовать так. Независимые циклы это простые циклы графа, отличающиеся друг от друга одним или более ребрами и не включающие в себя никакие другие независимые циклы.

Выполнив 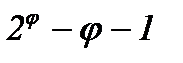раз операцию сложения по модулю два над независимыми циклами, получим все циклы графа.

Практическим применением цикломатического числа являются следующие утверждения:

1. Связный граф G не имеет циклов тогда и только тогда, когда j=0.

2. Связный граф G имеет единственный цикл тогда и только тогда, когда j=1.

3. Цикломатическое число связного графа можно определяет число ребер, которое нужно удалить, чтобы граф стал деревом.

 

V 2

V 1

V 5

V 4

V 3

 

Рисунок 2.8 – Неориентированный граф

 

Цикломатическое число графа, изображенного на рисунке 2.8 равно j=7-5+1= 3. Независимыми циклами графа являются: (v₁,v₃,v₄,v₁), (v₂,v₃,v₄,v₂), (v₅,v₃,v₄,v₅).

Обходы графа. Э йлеровым циклом называется такой цикл в конечном неориентированном графе, в который каждое ребро графа входит в точности 1 раз. Граф, содержащий такой цикл называется эйлеровым графом. Доказано, что конечный граф является эйлеровым тогда и только тогда, когда он связан и степени всех его вершин чётны.

Другим типом обхода графов являются гамильтоновы циклы. Простой цикл называется гамильтоновым, если он проходит через каждую вершину графа. В орграфах можно искать контуры (орциклы), проходящие через каждую вершину по одному разу.

Так называемая задача о коммивояжере (бродячем торговце), является задачей относящейся к гамильтоновым циклам. Коммивояжер должен посетить ряд городов, расстояния между которыми известны, и вернуться в исходный город. Нужно найти кратчайший путь, проходящий через все города.

 

 

Способы представления графов

 

Очевидно, что наиболее понятный и полезный для человека способ представления графа - изображение его на плоскости в виде окружностей (точек) и соединяющих их линий - будет совершенно бесполезным, если необходимо решать задачи, связанные с графами, с помощью ЭВМ.

Выбор соответствующей структуры данных для представления графов имеет принципиальное влияние на эффективность алгоритмов, поэтому машинное представление графов заслуживает специального рассмотрения. Будем рассматривать, как ориентированные, так и неориентированные графы.

Существует большое количество способов представления графов. Выделим из них четыре основных:

матрица смежности;

матрица инцидентности;

список пар вершин;

список смежности.

Матрица смежности

Одним из наиболее распространённых машинных представлений графа является матрица смежности.

Пусть дан граф G=(V,E), его матрица смежности обозначается A=(a_i,j) и определяется следующим образом:

a_i,j=1, если в G существует дуга (v_i,v_j), ведущая из вершины v_i в вершину v_j;

a_i,j= 0, если такой дуги в графе G не существует.

Например, для графа, изображённого на рис.2.10, матрица смежности имеет вид:

 

	V1	V2	V3	V4	V5
V1
V2
V3
V4
V5

 

 

V1

V5

V2

V4

V3

 

Рисунок 2.10 – Смешанный граф

 

Матрица смежности неориентированного графа является симметричной. При изображении матрицы вовсе необязательно указывать нумерацию вершин, важно считать нумерацию строк и столбов слева направо и сверху вниз в соответствии с номерами вершин, например та же матрица может иметь и такой вид:

 

 

Сеть G=(V,E,f), в которой дуге (ребру) 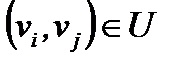сопоставлено число f_i,j=f(v_i,v_j), может быть представлена матрицей весов F=(f_ij), аналогичной матрице смежности, в которой вместо 1 записываются веса соответствующих ребер. Веса несуществующих (но потенциально возможных дуг или ребер) обычно полагают равными 0 или ¥, в зависимости от конкретного смысла задачи. Например, если f_i,j означает пропускную способность дуги ведущей из v_i в v_j, то равенство f_i,j =0 эквивалентно отсутствию пути из v_i в v_j. Если же f_i,j означает стоимость перемещения из пункта v_i в пункт v_j, то равенство f_i,j = указывает на невозможность перемещения в данном направлении.

На рисунке 2.11 изображена сеть, которую будем интерпретировать как информационную сеть. Пометки (веса) на дугах соответствуют пропускной способности каналов передачи данных, т. е. максимальному количеству некоторых единиц информации, которые могут быть переданы за единицу времени. Матрица весов сети в этом случае будет иметь вид:

 

¥
	∞
		¥
			¥

 

V1

V2

V4

V3

 

 

Рисунок 2.11 – Граф информационной сети

 

Если же эту сеть интерпретировать как информационную сеть, на которой требуется определить кратчайшие пути доставки сообщений между заданными узлами, а веса f_i,j как длины очередей сообщений к исходящим каналам, то матрица сети имеет вид:

 

			¥
¥
¥	¥

Матрица инцидентности

Для алгебраического задания графов может также использоваться матрица инцидентности B=(b_ij), элементы которой определяются следующим образом:

b_ij=-1, если v_i является начальной вершиной дуги e_j;

b_ij=1, если v_i является конечной вершиной дуги e_j;

b_ij=0, если вершина v_i и дуга e_j не инцидентны.

Поскольку каждая дуга простого орграфа инцидентна двум различным вершинам, каждый столбец матрицы B содержит один элемент, равный -1, и один – равный 1, все остальные элементы столбца равны 0.

Если G является неориентированным графом, то его матрица инциденций B=(b_ij) определяется соотношением

Для графа, содержащего петли, в соответствующих столбцах матрицы ставится только одна единица. Причем для ориентированной петли –1, а для неориентированной 1.

Матрица инцидентности графа приведённого на рис.10, имеет вид:

	u1,3	u1,4	u2,1	u2,4	U3,4	U3,5	u4,4	u4,5	U5,5
V1	-1
V2			-1
V3					-1
V4							-1	-1
V5

 

Для взвешенного графа (сети) в матрице инцидентности вместо единиц следует проставлять веса рёбер. например для графа на рисунке 2.11 матрица инцидентности будет иметь вид:

 

	U2,1	u1,2	u1,3	u2,3	U3,2	u2,4	u3,4	u4,3
V1		-1	-5
V2	-4			-3		-2
V3					-3		-6
V4								-4

 

Следует заметить, что представление графа с отрицательными весами дуг матрицей инцидентности невозможно, так как отрицательный вес приводит к изменению направления дуги и неоднозначности трактовки направления дуги.

Список пар вершин

Более экономным в смысле расхода памяти является метод представления графа с помощью списка пар вершин, соответствующим его ребрам. Список имеет размерность m×2 для неориентированного графа, m×3 для орграфа, m×4 для взвешенного графа. Первые два столбца содержат упорядоченные пары вершин (v_i,v_j), соответствующие рёбрам графа, в третьем столбце указывается признак ориентированности ребра 1 – для ориентированного ребра, 0 – для неориентированного, четвертый столбец содержит веса рёбер. Для графов рисунках 2.10 и 2.11 списки пар вершин будут соответственно иметь следующий вид:

 

 

Петля в списке отражается двумя одинаковыми вершинами в первом и втором столбце. Список пар вершин наилучшая форма для ввода графа в ЭВМ, однако при реализации алгоритмов на графах она менее всего удобна.

 

Список смежности

Список смежности содержит для каждой вершины, помеченной признаком "начало" (н), список вершин, смежных с данной вершиной. Каждый список вершин заканчивается признаком "конец" (к). Для графов на рис.2.10 и 2.11 списки смежности соответственно имеют вид:

 

н 1 - 3 - 4 к н 1 - 2 - 3 к

н 2 - 1 - 4 к н 2 - 1 - 3 - 4 к

н 3 - 4 - 5 к н 3 - 2 - 4 к

н 4 – 1 - 2 – 4 - 5 к н 4 - 3 к

н 5 – 3 – 5 к.

Описание графа в виде списка смежности благодаря признакам "н" и "к" может выполняться не в виде таблицы, а в виде строки, что позволяет значительно экономить занимаемую описанием графа память ЭВМ. Так же программисты часто используют такую форму представления без указания признаков "н" и "к", а просто задавая смежные вершины для каждой вершины графа без отображения их самих, что также экономит память компьютера. Например те же списки смежности будут иметь следующий вид:

3,4 2,3

1,4 1,3,4

4,5 2,4

1,2,4,5 3

3,5

Здесь номер строки соответствует номеру вершины.

В дальнейшем, рассматривая алгоритмы, работающие с графами, будем определять наиболее удобные описания для каждого конкретного случая. Причем следует иметь ввиду, что не каждую структуру графа можно представить любым из рассмотренных способов. Подумайте над этим самостоятельно.

 

Лекция Связность графов

1. Методы определения связности вершин графа.

2. Построение минимального покрывающего дерева.