Знакомство с количественными соотношениями начинается с прямого счета: 1, 2, 3, 4, 5, …. Им пользуются при определении количества однородных предметов: тетрадей, книг, CD дисков и т. д. Результат достигается сложением положительных целых чисел. Например, следующее за числом 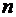 число
число 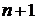 получается прибавлением единицы к
получается прибавлением единицы к 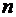 . Все такие числа образуют совокупность (множество) натуральных чисел, которое обозначается заглавной буквой
. Все такие числа образуют совокупность (множество) натуральных чисел, которое обозначается заглавной буквой 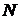 латинского алфавита:
латинского алфавита:
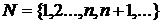 (1)
(1)
В фигурных скобках указаны элементы этого множества.
Определение–пояснение: множеством называют совокупность однородных элементов, объединенных общим свойством или признаком.
Обратный счет встречается при решении задач, связанных с вычитанием из одного натурального числа второго. Например, вычитая из числа 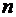 единицу, получим число
единицу, получим число 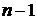 . Вычитая единицу
. Вычитая единицу 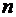 раз, подряд, из числа
раз, подряд, из числа 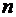 , получим число «0», обозначающее отсутствие перечисляемых предметов, их количество равно нулю. Дальнейшее вычитание приводит к отрицательным числам:
, получим число «0», обозначающее отсутствие перечисляемых предметов, их количество равно нулю. Дальнейшее вычитание приводит к отрицательным числам: 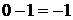 ,
, 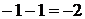 ≡
≡ 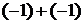 и т. д. Вычитание обратно сложению. Так равенству
и т. д. Вычитание обратно сложению. Так равенству 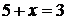 отвечает число
отвечает число 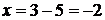 , получаемое вычитанием большего числа 5 из меньшего числа 3. Натуральные числа, число «0» и отрицательные целые числа образуют множество целых чисел. Это множество обозначают заглавной буквой
, получаемое вычитанием большего числа 5 из меньшего числа 3. Натуральные числа, число «0» и отрицательные целые числа образуют множество целых чисел. Это множество обозначают заглавной буквой 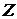 латинского алфавита:
латинского алфавита:
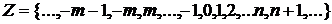 (2)
(2)
Арифметическая операция «умножение» является сокращенной записью сложения одинаковых чисел. Так запись 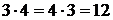 , не зависящая от порядка множителей, обозначает равные количества, получаемые сложением или четырех чисел 3, или трех чисел 4:
, не зависящая от порядка множителей, обозначает равные количества, получаемые сложением или четырех чисел 3, или трех чисел 4: 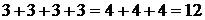 .
.
Операция «деление» появляется, как операция обратная умножению. Уравнение 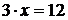 обращается в тождество для значения
обращается в тождество для значения 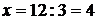 . Но не всегда уравнение
. Но не всегда уравнение 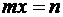 , где
, где 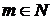 и
и 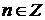 , имеет решением число
, имеет решением число 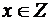 . Когда
. Когда 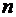 не делится без остатка на
не делится без остатка на 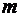 , получаем нецелое число
, получаем нецелое число
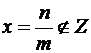 (3)
(3)
“Довиетовские” алгебраисты ограничивались заявлением, что «такое деление не возможно». Сейчас это рациональные числа.
Несократимые (положительные и отрицательные) дроби 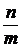 , где
, где 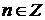 ,
, 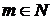 , дают множество рациональных чисел, которое обозначают заглавной буквой
, дают множество рациональных чисел, которое обозначают заглавной буквой 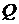 латинского алфавита,
латинского алфавита, 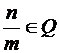 . Все рациональные числа представляются периодическими десятичными дробями. Так, 2/3 = 0,66666… = 0,(6).
. Все рациональные числа представляются периодическими десятичными дробями. Так, 2/3 = 0,66666… = 0,(6).
Степень числа – это сокращённая запись умножения нескольких одинаковых чисел. Так, при определении, например, общей длины приставленных друг к другу трех одинаковых стержней, по 3 см каждый, мы получим 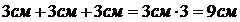 . Для математики не существенны единицы измерения складываемых однородных величин, то есть величин одинаковой размерности. Важны только количественные соотношения. Тогда в нашем случае
. Для математики не существенны единицы измерения складываемых однородных величин, то есть величин одинаковой размерности. Важны только количественные соотношения. Тогда в нашем случае 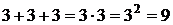 , и говорят: «три в степени 2 равно 9». В общем случае произведение
, и говорят: «три в степени 2 равно 9». В общем случае произведение 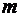 одинаковых чисел «
одинаковых чисел «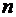 » записывают сокращенно, как «
» записывают сокращенно, как «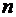 » в степени
» в степени 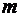 , то есть
, то есть 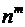 , где «
, где «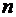 » – основание и
» – основание и 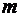 – степень.
– степень.
Для операции «возведение в степень» обратной будет операция «извлечение корня». Так, для 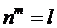 извлечённым корнем будет:
извлечённым корнем будет: 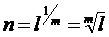 . Говорят: «корень
. Говорят: «корень 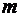 -ой степени из числа
-ой степени из числа 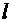 ». Операция «извлечение корня» записывает решение уравнения:
». Операция «извлечение корня» записывает решение уравнения: 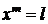 . Замечание: когда
. Замечание: когда 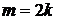 – четное число, тогда
– четное число, тогда 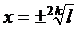 , так как проверка даёт
, так как проверка даёт 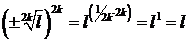 .
.
В отличие от уравнения 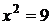 с решениями
с решениями 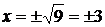 , для которых
, для которых 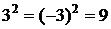 , решениями уравнения
, решениями уравнения 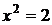 являются числа
являются числа 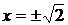 . Они уже не принадлежат ни множеству целых, ни множеству рациональных чисел,
. Они уже не принадлежат ни множеству целых, ни множеству рациональных чисел, 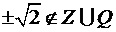 . Знак «
. Знак «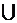 » обозначает объединение множеств
» обозначает объединение множеств 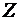 и
и 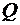 . Такие числа, как:
. Такие числа, как: 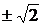 ,
, 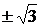 ,… число «
,… число «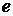 », число «
», число «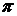 » и др. представляются бесконечными непериодическими дробями. Их объединяют в множество иррациональных чисел, обозначаемое заглавной буквой
» и др. представляются бесконечными непериодическими дробями. Их объединяют в множество иррациональных чисел, обозначаемое заглавной буквой 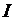 латинского алфавита.
латинского алфавита.
Иррациональное число появляются, например, когда несколько отрезков «несоизмеримы». Для них нельзя найти отрезок конечной длины, укладывающийся целое число раз в каждом из измеряемых отрезков. Так, иррациональность числа 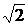 связана с несоизмеримостью катетов равнобедренного прямоугольного треугольника с его гипотенузой;
связана с несоизмеримостью катетов равнобедренного прямоугольного треугольника с его гипотенузой; 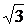 – иррациональное число, так как ребра куба несоизмеримы с его объемной диагональю; число
– иррациональное число, так как ребра куба несоизмеримы с его объемной диагональю; число 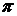 – иррациональное число вследствие несоизмеримости длины окружности с ее диаметром. Число
– иррациональное число вследствие несоизмеримости длины окружности с ее диаметром. Число 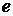 тоже иррациональное число, так как оно по определению равно бесконечной сумме убывающих рациональных чисел:
тоже иррациональное число, так как оно по определению равно бесконечной сумме убывающих рациональных чисел:
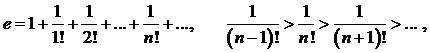 , (4)
, (4)
где 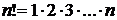 , читают «число эн факториал». «Эн факториал» равен произведению всех натуральных чисел от 1 до
, читают «число эн факториал». «Эн факториал» равен произведению всех натуральных чисел от 1 до 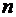 . По определению 0! ≡ 1.
. По определению 0! ≡ 1.
Объединённая совокупность целых, рациональных и иррациональных чисел образуют множество действительных чисел. Его обозначают заглавной буквой 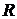 латинского алфавита:
латинского алфавита:
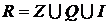 . (5)
. (5)
Важно, что действительные числа «сплошь » заполняют числовую ось. То есть между любыми двумя сколь угодно близкими числами 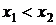 можно вставить бесконечное число действительных чисел. Аналогичным свойством обладают и рациональные числа: «между двумя не равными рациональными числами всегда можно вставить тоже рациональное число». Это свойство действительных (и рациональных) чисел играет «важную» роль в теории пределов, изучаемой в этом семестре. Но вычисления на ЭВМ нарушают это свойство действительных чисел. Дело в том, что машинное представление числа с конечной мантиссой и порядком всегда содержит только конечное число чисел. А множества чисел, которыми мы пользуемся, бесконечные. Это может привести к ошибочному результату при решении на ЭВМ и нелинейных уравнений, и систем линейных уравнений, и дифференциальных уравнений. Об этом, по крайней мере, нужно знать и, по возможности, проверять полученное решение на «здравый смысл », а в определенных частных случаях проверять и его совпадение с уже имеющимися очевидными результатами.
можно вставить бесконечное число действительных чисел. Аналогичным свойством обладают и рациональные числа: «между двумя не равными рациональными числами всегда можно вставить тоже рациональное число». Это свойство действительных (и рациональных) чисел играет «важную» роль в теории пределов, изучаемой в этом семестре. Но вычисления на ЭВМ нарушают это свойство действительных чисел. Дело в том, что машинное представление числа с конечной мантиссой и порядком всегда содержит только конечное число чисел. А множества чисел, которыми мы пользуемся, бесконечные. Это может привести к ошибочному результату при решении на ЭВМ и нелинейных уравнений, и систем линейных уравнений, и дифференциальных уравнений. Об этом, по крайней мере, нужно знать и, по возможности, проверять полученное решение на «здравый смысл », а в определенных частных случаях проверять и его совпадение с уже имеющимися очевидными результатами.
Стоит отметить, что расширение числового «множества» от натуральных чисел до действительных чисел не является произвольным. Несмотря на ожидаемое появление «более сложных» множеств чисел по мере включения в рассмотрение новых типов задач и новых уравнений, например, степенных, показательных и т. д., такие усложнения не могут быть произвольными…
«В природе» имеется некий механизм (схема) расширения числового множества (числового поля). Фундаментальная идея, дающая такую общую схему, сформулирована немецким математиком Германом Хенкелем в 1867 г. Её элементы ранее рассматривал Уильям Гамильтон. Её называют «принципом перманентности ». Согласно этой схеме:
1. Среди элементов расширенного числового множества содержится последовательность натуральных чисел.
2. Есть критерий, устанавливающий равенство или неравенство всех элементов числового множества, а в случае, когда элементы являются натуральными числами, этот критерий превращается в известное правило сравнения натуральных чисел.
3. Для любых двух элементов множества задаётся схема сложения и умножения, подчиняющаяся перестановочному, сочетательному и распределительному законам. Она обязательно превращается в схему действия над натуральными числами, когда элементы множества являются таковыми.
Комплексные числа.
Дальнейшее расширение числового «множества» связано с рассмотрением задач, которые на множестве действительных чисел не имеют решения. Например, уже простейшее квадратное уравнение
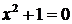 , (6)
, (6)
не имеет решения на множестве действительных чисел. Ясно, что квадрат любого действительного числа не может быть числом отрицательным, и оно в сумме с положительным числом 1 дает число большее нуля, 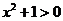 ? Но если
? Но если 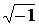 считать, по определению, числом, называемым «мнимой единицей», уравнение (6) обращается в тождество при таком х =
считать, по определению, числом, называемым «мнимой единицей», уравнение (6) обращается в тождество при таком х = 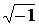 . Обозначают это число буквой
. Обозначают это число буквой 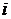 .
.
Тогда, согласно (6), основное свойство числа 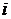 :
:
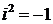 . (7)
. (7)
Решением аналогичного уравнения 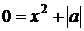 теперь будет
теперь будет 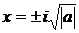 . Проверку результата даёт тождество:
. Проверку результата даёт тождество: 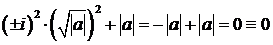 .
.
Определение функции 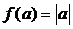 , читают «модуль числа
, читают «модуль числа 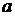 »:
»:
Модуль любого действительного числа 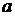 ,
, 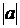 , всегда имеет неотрицательное значение, получаемое согласно следующему «предписанию»:
, всегда имеет неотрицательное значение, получаемое согласно следующему «предписанию»:
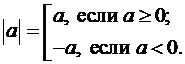 . (8)
. (8)
Усложним задачу. Решим теперь квадратное уравнение
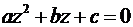 , (9)
, (9)
Для любых 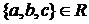 . Известно, что оно имеет действительное решение
. Известно, что оно имеет действительное решение
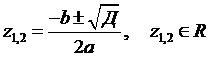 , (10)
, (10)
если дискриминант уравнения 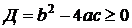 , и такого решения нет, если иначе. Но применение в случае
, и такого решения нет, если иначе. Но применение в случае 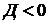 мнимой единицы со свойством (7) позволяет явно записать
мнимой единицы со свойством (7) позволяет явно записать 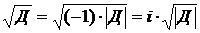 и получить явные решения уравнения (9) в виде двух новых, комплексных,чисел с мнимой единицей:
и получить явные решения уравнения (9) в виде двух новых, комплексных,чисел с мнимой единицей:
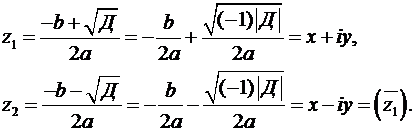 ; (10´)
; (10´)
В комплексных числах 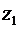 и
и 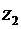
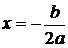 – их действительная часть. Их записывают, как
– их действительная часть. Их записывают, как 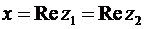 . Далее,
. Далее,  – мнимая часть комплексного числа
– мнимая часть комплексного числа 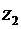 и
и 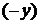 – мнимая часть комплексного числа
– мнимая часть комплексного числа 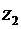 . Это записывают, как
. Это записывают, как 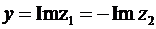 . Числа
. Числа 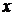 и
и 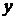 в (10´) вещественные,
в (10´) вещественные, 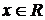 и
и 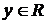 .
.
Числа 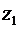 и
и 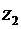 называют комплексно сопряженными. Обозначают комплексное сопряжение или «*» справа вверху от числа, или чертой над ним
называют комплексно сопряженными. Обозначают комплексное сопряжение или «*» справа вверху от числа, или чертой над ним
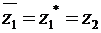 ,
, 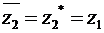 . (11)
. (11)
Операция комплексного сопряжения меняет только знак мнимой части комплексного числа z на противоположный знак (см. равенства (10´)).
Каждую формулу (10´) надо считать, как единую запись комплексного числа в координатной форме. Это одно число, состоящее из двух частей:
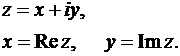 . (12)
. (12)
Комплексное число 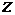 , у которого отлична от нуля мнимая часть,
, у которого отлична от нуля мнимая часть, 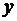 =
= 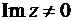 , называют существенно комплексным числом.
, называют существенно комплексным числом.
Модулем комплексного числа (12) называют неотрицательное значение
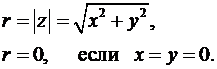 (13)
(13)
Каждому комплексному числу, записанному в форме (12), соответствует упорядоченная пара вещественных чисел: 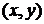 . Эту упорядоченную пару чисел можно рассматривать и, как координаты точки
. Эту упорядоченную пару чисел можно рассматривать и, как координаты точки 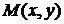 на ортогональной декартовой плоскости
на ортогональной декартовой плоскости 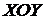 , и, как декартовые координаты вектора
, и, как декартовые координаты вектора 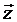 , проведенного из начала ортогональной системы в точку
, проведенного из начала ортогональной системы в точку 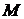 . Наоборот каждой точке
. Наоборот каждой точке 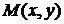 и, соответственно, вектору
и, соответственно, вектору 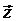 равенство (12) ставит в соответствие комплексное число
равенство (12) ставит в соответствие комплексное число 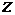 ,
, 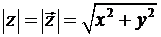 . Горизонтальную ось О х «комплексной плоскости» обозначают
. Горизонтальную ось О х «комплексной плоскости» обозначают 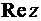 , а мнимую ось О у –
, а мнимую ось О у – 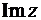 .
.
Угол 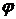 , который радиус-вектор
, который радиус-вектор 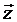 образует с положительной осью О х, называют аргументом комплексного числа
образует с положительной осью О х, называют аргументом комплексного числа 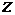 и обозначают
и обозначают 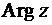 . Поворот радиус вектора
. Поворот радиус вектора 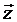 на угол
на угол 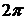 даёт то же значение (12) комплексного числа. Поэтому значение
даёт то же значение (12) комплексного числа. Поэтому значение 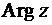 для комплексного числа
для комплексного числа 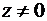 определяется с точностью до целочисленного значения
определяется с точностью до целочисленного значения 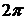 ,
, 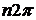 . Если значение
. Если значение 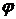 аргумента комплексного числа такое, что
аргумента комплексного числа такое, что 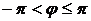 , его обозначают
, его обозначают 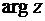 . Ясно, что
. Ясно, что
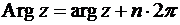 ,
, 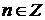 (14)
(14)
Поскольку период функции 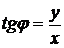 равен
равен 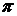 , что меньше 2
, что меньше 2 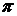 в (14), в применениях обратной тригонометрической функции
в (14), в применениях обратной тригонометрической функции  для определения
для определения 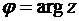 надо «компенсировать » это свойство функции
надо «компенсировать » это свойство функции 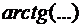 , т.е.:
, т.е.:
 , (15)
, (15)
где 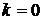 , если точка
, если точка 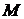 находится в 1-ой и 4-ой четвертях,
находится в 1-ой и 4-ой четвертях, 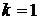 , если точка
, если точка 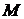 из второй четверти, и
из второй четверти, и 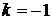 , когда точка
, когда точка 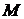 находится в 3-ей четверти.
находится в 3-ей четверти.
Для прямоугольного треугольника 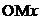 (см. ниже Рис. 1) можно записать очевидные тождества с тригонометрическими функциями
(см. ниже Рис. 1) можно записать очевидные тождества с тригонометрическими функциями 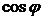 и
и 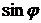 ,
,
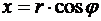 ,
, 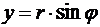 (16)
(16)
Их применение в (12) даёт тригонометрическую форму комплексного числа:
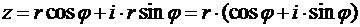 . (17)
. (17)

Рисунок 1.
Замена в (17) 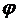 на
на 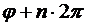 , где
, где 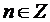 , вследствие периодичности тригонометрических функций не изменяет значение числа
, вследствие периодичности тригонометрических функций не изменяет значение числа 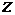 .
.
Определение: Два комплексных числа равны, если, соответственно, равны их действительные и мнимые части.
После применения в (17) известной формулы Эйлера
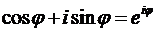 , (18)
, (18)
получим экспоненциальную, показательную, форму комплексного числа
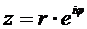 . (19)
. (19)
Формула (18) будет доказана в теории рядов Тейлора. Она следует из равенства рядов, представляющих левую и правую части этого тождества. (Числовые и функциональные ряды изучаются во втором семестре).
Связь между комплексными числами и векторами на плоскости (с их проекциями на координатные оси) становится полной после определения операции сложения комплексных чисел, 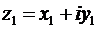 и
и 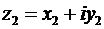 :
:
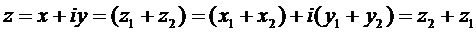 . (20)
. (20)
Разность комплексных чисел определяется, как операция обратная сложению: 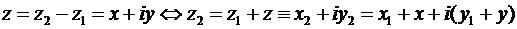 , где знак «
, где знак «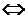 » обозначает «равносильность» равенств. Отсюда
» обозначает «равносильность» равенств. Отсюда 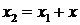 ,
, 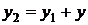 . Решение этих уравнений даёт
. Решение этих уравнений даёт
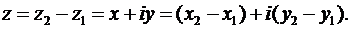 (21)
(21)
Равенства (20) и (21) полностью совпадают с равенствами для проекций суммы и разности двух векторов, что иллюстрируют рисунки 2 и 3.
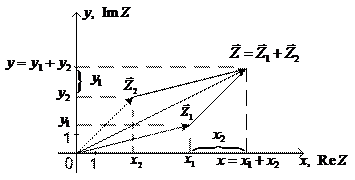
Рисунок 2.
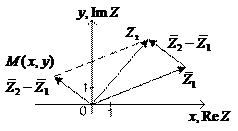
Рисунок 3.
На рисунке 3 в точку  направлен вектор
направлен вектор 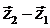 , который однозначно соответствует разности комплексных чисел
, который однозначно соответствует разности комплексных чисел 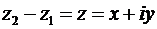 , определяемой по формуле (21). Взаимное соответствие между комплексными числами и векторами на плоскости, с точностью до их сложения и вычитания, называют изоморфизмом множеств комплексных чисел и векторов на плоскости.
, определяемой по формуле (21). Взаимное соответствие между комплексными числами и векторами на плоскости, с точностью до их сложения и вычитания, называют изоморфизмом множеств комплексных чисел и векторов на плоскости.
Этот изоморфизм используется, например, в электротехнике. Расчеты сложных электрических цепей с равным успехом проводят и «методом векторных диаграмм», и «методом комплексных амплитуд». Результат тот же.
Произведение двух комплексных чисел определяется как алгебраическая операция умножения двучлена 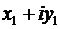 на двучлен
на двучлен 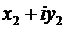 . После учёта
. После учёта 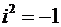 и приведения подобных отдельно для величин, не содержащих множителем мнимую единицу
и приведения подобных отдельно для величин, не содержащих множителем мнимую единицу 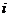 , и для величин, содержащих её, получаем
, и для величин, содержащих её, получаем
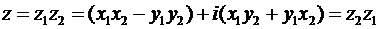 . (22)
. (22)
Применение тригонометрической или показательной форм записи чисел: 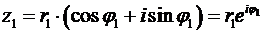 ,
, 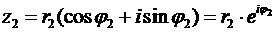 подтверждает правило (22). Действительно, для их произведения получаем
подтверждает правило (22). Действительно, для их произведения получаем
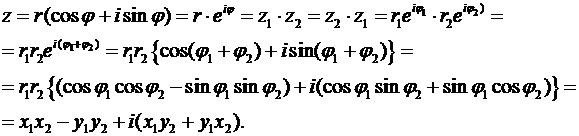 (23)
(23)
Модуль числа 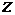 в (23) равен произведению модулей перемножаемых комплексных чисел,
в (23) равен произведению модулей перемножаемых комплексных чисел, 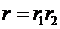 , а его аргумент φ – сумме аргументов,
, а его аргумент φ – сумме аргументов, 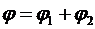 .
.
По правилу умножения комплексных чисел (23) можем записать m- ую степень для комплексного числа 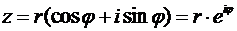 :
:
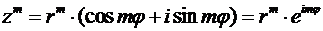 . (24)
. (24)
При 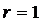 из (24) следует известная формула Муавра:
из (24) следует известная формула Муавра:
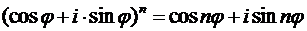 , (24′)
, (24′)
для любого целого показателя степени 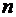 .
.
Операция деления комплексных чисел определяется, как операция обратная операции их умножения. Равенство 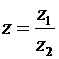 равносильно равенству
равносильно равенству 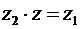 . Тогда верно:
. Тогда верно: 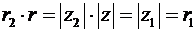 и
и 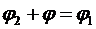 . Отсюда следует:
. Отсюда следует: 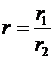 ,
, 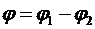 . Поэтому для частного
. Поэтому для частного 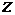 можем записать:
можем записать:
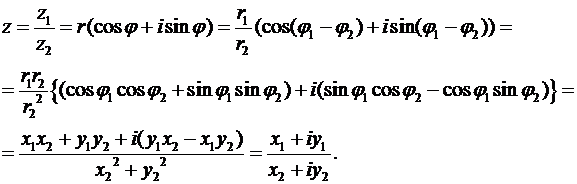 (25)
(25)
При переходе к координатной записи для результата деления (25) и умножения (23) комплексных чисел здесь применены равенства: 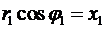 ,
, 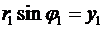 ,
, 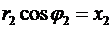 и
и 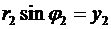 .
.
Операция «извлечение корня» – это операция обратная «степени числа». Но в пространстве комплексных чисел извлечение корня любой степени уже не является однозначной операцией. Действительно, то, что число 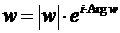 является корнем
является корнем 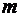 -ой степени
-ой степени 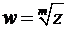 из комплексного числа
из комплексного числа 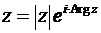 , равносильно
, равносильно 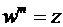 . Отсюда для их модулей и аргументов (сравни (18) и (24)) верны равенства:
. Отсюда для их модулей и аргументов (сравни (18) и (24)) верны равенства:
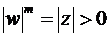 ,
, 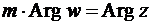 . (26)
. (26)
Вследствие неоднозначности 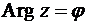 и
и 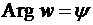 (см. (14)) тождество для аргументов в (26) следует рассматривать, как равенство множеств:
(см. (14)) тождество для аргументов в (26) следует рассматривать, как равенство множеств:
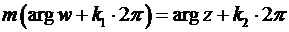 ,
, 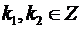 . (27)
. (27)
Поэтому из первого уравнения (26) получаем одно значение модуля
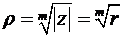 . (26′)
. (26′)
А из равенств (27) имеем 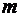 значений аргумента корня,
значений аргумента корня, 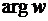 , интервал изменения которого не превышает
, интервал изменения которого не превышает 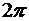 . Разные
. Разные 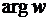 различает индекс
различает индекс 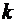 :
:
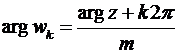 ,
, 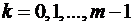 , где
, где 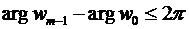 . (27′)
. (27′)
Общая формула для 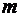 различных значений корня из комплексного числа:
различных значений корня из комплексного числа:
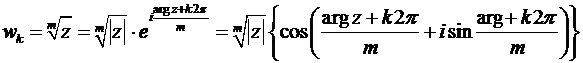 . (28)
. (28)
В ней 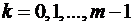 . Возведение каждого корня (28) в
. Возведение каждого корня (28) в 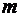 -ую степень даёт
-ую степень даёт 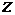 . Соединив начало координат плоскости
. Соединив начало координат плоскости 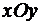 , где
, где 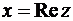 и
и 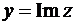 , с точками
, с точками 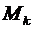 , изображающими комплексные числа
, изображающими комплексные числа 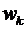 (28), получим
(28), получим 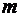 -конечную звезду (см., например, ниже Рис. 4). Её лучи равны, потому что у всех
-конечную звезду (см., например, ниже Рис. 4). Её лучи равны, потому что у всех 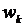 одинаковые значения модуля
одинаковые значения модуля 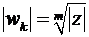 .
.
Пример 1. Для комплексного числа 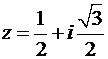 найти модуль и аргумент, записать его в тригонометрическом и экспоненциальном виде. Определить все корни 5-ой степени из этого комплексного числа.
найти модуль и аргумент, записать его в тригонометрическом и экспоненциальном виде. Определить все корни 5-ой степени из этого комплексного числа.
Решение.
Модуль числа равен:
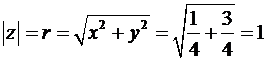
Так как 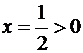 ,
, 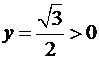 и поэтому точка
и поэтому точка 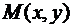 лежит в первой четверти, то в формуле (15)
лежит в первой четверти, то в формуле (15) 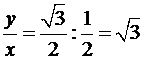 и
и 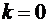 :
:
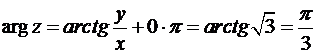 .
.
Запишем это число в тригонометрическом и экспоненциальном виде:
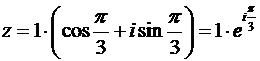 .
.
Вычислим модуль для корня 5-ой степени из числа 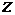 по формуле (26′)
по формуле (26′)
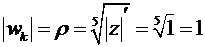 .
.
По формуле (27′) мы получим пять различных значений аргумента, разность между которыми не превышает 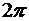 ,
,
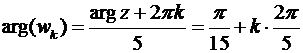 ,
, 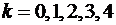 .
.
Из-за 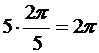 , значение корня с
, значение корня с 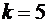 повторяет его значение с
повторяет его значение с 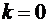 :
: 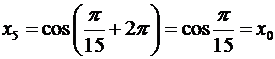 и
и 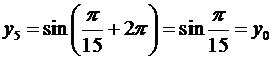 . Равна и следующая пара корней. Поэтому только 5 различных значений корня:
. Равна и следующая пара корней. Поэтому только 5 различных значений корня:
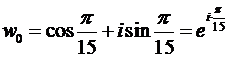 ,
,
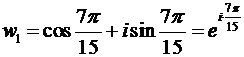 ,
,
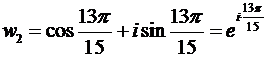 ,
,
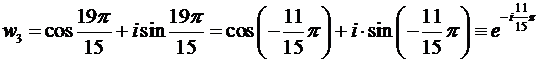 ,
,
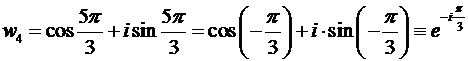 .
.
В записанных формулах значения 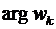 приведены к стандартному интервалу:
приведены к стандартному интервалу: 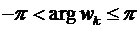 ,
, 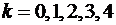 . Точки
. Точки 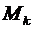 комплексной плоскости, соответствующие комплексным числам
комплексной плоскости, соответствующие комплексным числам 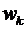 , делят окружность радиуса
, делят окружность радиуса 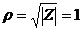 с центром в начале координат на пять равных дуг (см. Рис. 4).
с центром в начале координат на пять равных дуг (см. Рис. 4).

Рисунок 4.
Задача решена.
Операция комплексного сопряжения (11) связана с заменой 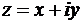 на
на 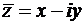 . Такой операции отвечает отражение вектора
. Такой операции отвечает отражение вектора 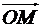 на Рис. 5 относительно оси
на Рис. 5 относительно оси 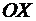 . После отражения он совпадает с вектором
. После отражения он совпадает с вектором 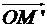 .
.
Комплексное сопряжение над результатом каждого арифметического действия равносильно замене всех комплексных чисел, участвующих в нём, на комплексно сопряженные числа. Соответствующее отражение всех векторов относительно оси 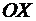 для операции сложения проиллюстрировано на Рис. 5. Отражение всех сторон параллелограмма относительно оси О х приводит к отражению относительно этой оси и всего параллелограмма (Рис. 5).
для операции сложения проиллюстрировано на Рис. 5. Отражение всех сторон параллелограмма относительно оси О х приводит к отражению относительно этой оси и всего параллелограмма (Рис. 5).
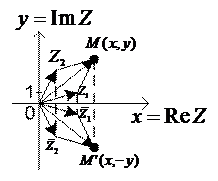
Рисунок 5.
Ниже приведены все тождества для арифметических операций, связанные с операцией комплексного сопряжения:
1) 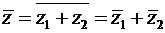 ,
,
2) 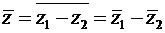 ,
,
3) 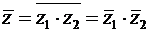 ,
,
4) 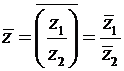 , (29)
, (29)
5) 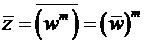 ,
,
6) 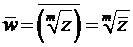 ,
,
7) 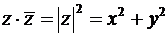 .
.
Тождество 1) и аналогично тождество 2) легко доказать геометрически, что и проиллюстрирует рисунок 5.
Тождества 3), 4), 5) и 6), 7) легко доказываются с помощью тригонометрической записи комплексного числа. Например,
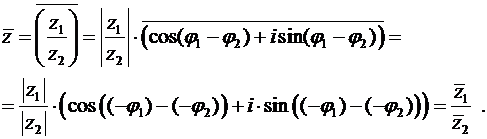
Другие функции комплексного аргумента будут рассмотрены позже.
Замечание: При выполнении операций сложения и вычитания удобнее применять координатную запись комплексного числа, 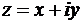 , а при умножении, делении, возведении в степень или при извлечении корня из комплексного числа удобнее применять тригонометрическую или показательную запись комплексного числа,
, а при умножении, делении, возведении в степень или при извлечении корня из комплексного числа удобнее применять тригонометрическую или показательную запись комплексного числа, 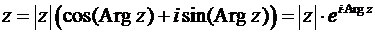 .
.
Равенство комплексных чисел, 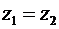 , как и векторов,
, как и векторов, 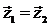 , связано с равенством их координат:
, связано с равенством их координат: 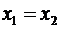 и
и 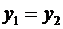 . Равносильные им равенства:
. Равносильные им равенства: 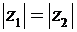 и
и 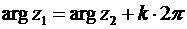 ,
, 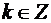 . Изоморфные этим комплексным числам вектора также равны, если равны их длины и направления.
. Изоморфные этим комплексным числам вектора также равны, если равны их длины и направления.
Замечание: Из изоморфизма комплексных чисел и векторов на плоскости следует, что комплексные числа можно сравнивать только по модулю. То есть можно проверить выполнение неравенства 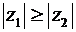 или
или 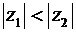 , но неравенства
, но неравенства 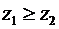 и
и 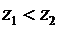 не имеют смысла. Это нужно учитывать при решении уравнений или неравенств, содержащих комплексные числа.
не имеют смысла. Это нужно учитывать при решении уравнений или неравенств, содержащих комплексные числа.
«Принцип перманентности » Германа Хенкеля выполняется для множества комплексных чисел. Поэтому оно является допустимым расширением множества вещественных чисел. Проверим это. Во первых, множество комплексных чисел содержит последовательность натуральных чисел с у = 0 и х = 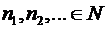 :
: 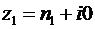 ,
, 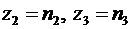 ,.... Во вторых, для множества таких чисел, из
,.... Во вторых, для множества таких чисел, из 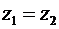 следует
следует 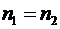 , и
, и 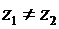 верно при
верно при 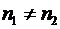 . В третьих, схемы их сложения (20) и умножения (22) переходят в схемы умножения
. В третьих, схемы их сложения (20) и умножения (22) переходят в схемы умножения 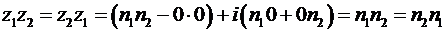 и схемы сложения
и схемы сложения 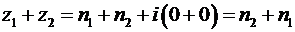 натуральных чисел, подчиняющиеся перестановочному, сочетательному и распределительному законам.
натуральных чисел, подчиняющиеся перестановочному, сочетательному и распределительному законам.
Пример 2. Вычислить: 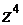 , если
, если 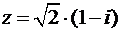 .
.
Решение:
Для 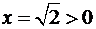 и
и 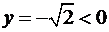 число
число 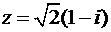 принадлежит четвертой четверти комплексной плоскости и поэтому в формуле (15)
принадлежит четвертой четверти комплексной плоскости и поэтому в формуле (15) 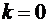 :
:
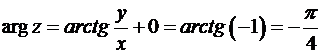 .
.
По определению (13):
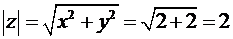 .
.
Теперь запишем  в показательной и тригонометрической форме:
в показательной и тригонометрической форме:
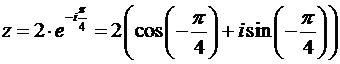 .
.
По правилу (24) вычислим так же степень комплексного числа:
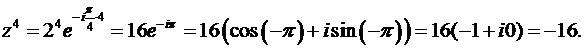
Задача решена.
Пример 3. Решить уравнение: 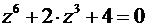 .
.
Решение:
Пусть 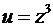 , тогда квадратное уравнение
, тогда квадратное уравнение 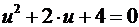 имеет дискриминант
имеет дискриминант 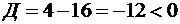 .
.
Поэтому для него получим два комплексно сопряженных решения:
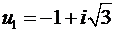 ;
; 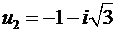 , где
, где  .
.
Учитывая обозначение 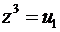 и формулу (28) для корня комплексного числа получим три значения
и формулу (28) для корня комплексного числа получим три значения 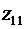 ,
, 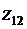 и
и 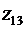 для кубического корня из
для кубического корня из 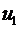 и три значения
и три значения 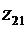 ,
, 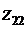 ,
, 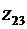 для кубического корня из комплексного числа
для кубического корня из комплексного числа 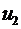 .
.
Для 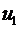 :
: 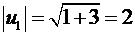 ,
, 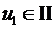 -ой четверти, в формуле (13)
-ой четверти, в формуле (13) 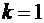 и поэтому
и поэтому 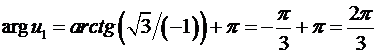 .
.
По формулам (28) получаем:
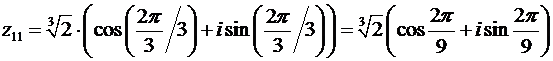 ,
,
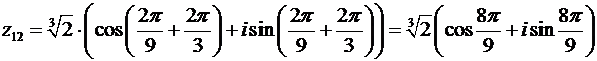 ,
,
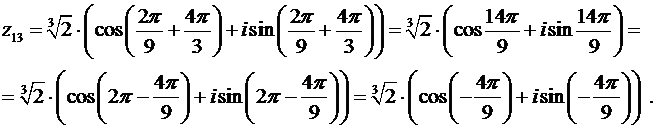 Здесь учтено стандартное ограничение на допустимые значения
Здесь учтено стандартное ограничение на допустимые значения 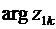 :
:
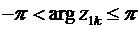 .
.
Решая аналогичное уравнение 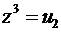 , получаем что
, получаем что 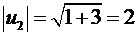 ,
, 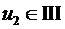 -ей четверти, в (13)
-ей четверти, в (13) 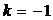 и
и 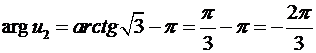 .
.
В этом случае из формул (28) следует:
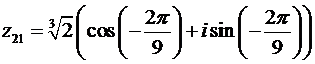 ,
,
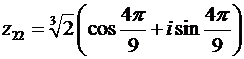 ,
,
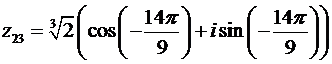 .
.
Всем решениям уравнения отвечают точки, лежащие на круге радиуса  с центром в начале координат комплексной плоскости (см. Рис. 6).
с центром в начале координат комплексной плоскости (см. Рис. 6).
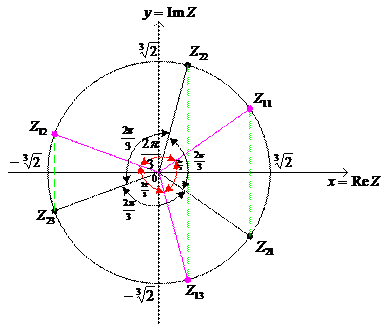
Рисунок 6.
Задача решена.
Пример 4. Решить неравенство: 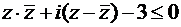 .
.
Решение:
Такое неравенство имеет смысл, если его можно свести к неравенству для модуля комплексного числа.
Учитывая, что согласно (10) 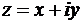 и
и 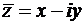 , получим неравенство
, получим неравенство  . Оно не содержит мнимой единицы и превращается в неравенство только для вещественных координат точек плоскости, которое ограничивает их допустимые значения:
. Оно не содержит мнимой единицы и превращается в неравенство только для вещественных координат точек плоскости, которое ограничивает их допустимые значения:
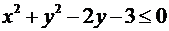 .
.
Выделяя полные квадраты, получим эквивалентное неравенство
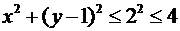 , (*)
, (*)
Оно эквивалентно неравенству 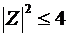 для модуля комплексного числа
для модуля комплексного числа 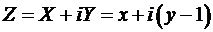 , поэтому неравенство (*) имеет решение.
, поэтому неравенство (*) имеет решение.
В случае равенства в (*) из него следует уравнение окружности
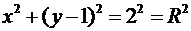 (**)
(**)
радиуса 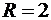 с координатами её центра:
с координатами её центра: 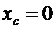
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2022-11-01 Нарушение авторских прав и Нарушение персональных данных