Гиперболическая функция.

Найти приближенное выражение функции в виде гиперболы .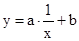

Решение:

1. Вводим исходные данные:

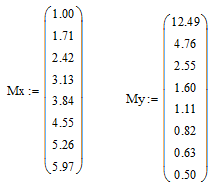
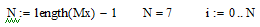
2. Находим параметры гиперболической функции:

Задание для индивидуального выполнения по вариантам:

	№	Исходные данные для аппроксимации методом наименьших квадратов
Буланов		x	1,20	1,57	1,94	2,31	2,68	3,05	3,42	3,79
y	2,59	2,06	1,58	1,25	0,91	0,66	0,38	0,21
Вакуленко		x	-4,38	-3,84	-3,23	-2,76	-2,22	-1,67	-1,13	-0,60
y	2,25	2,83	3,44	4,31	5,29	6,55	8,01	10,04
Воронов		x	1,00	1,64	2,28	2,91	3,56	4,19	4,84	5,48
y	0,28	0,19	0,15	0,11	0,09	0,08	0,07	0,06
Вылегжанин		x	5,84	3,82	6,19	9,22	7,87	6,29	4,43	8,91
y	79,31	57,43	60,66	91,55	90,12	71,30	4,43	91,25
Голованов		x	2,91	2,94	6,35	6,58	3,80	6,43	0,57	5,96
y	82,16	61,02	44,56	84,52	99,17	70,24	63,23	66,48
Гурнутин		x	5,46	2,73	6,49	4,26	2,39	6,46	0,86	2,06
y	65,72	58,05	60,05	55,79	50,83	47,69	44,79	59,74
Ибрагимов		x	1,28	1,76	2,24	2,72	3,20	3,68	4,16	4,64
y	2,10	2,62	3,21	3,96	4,98	6,06	4,47	9,25
Исенгалиев		x	-4,84	-4,30	-3,6	-3,22	2,68	-2,14	-1,60	-1,06
y	-0,09	-0,11	-0,13	-0,16	-0,19	-0,26	-0,39	-0,81
Кожевников		x	3,54	4,29	4,78	3,99	1,13	6,29	1,89	3,27
y	22,81	28,42	24,95	26,96	8,78	33,55	15,77	22,89
Конистратенко		x	4,08	4,42	2,52	-0,08	2,14	3,36	7,35	5,00
y	18,31	21,85	19,93	-8,23	10,90	17,18	36,45	24,11
Коркин		x	1,16	1,88	2,60	-3,32	4,04	4,76	5,48	6,20
y	0,18	0,26	0,32	0,36	0,40	0,43	0,95	0,85
Лашманов		x	1,00	1,71	2,42	-3,13	3,84	4,55	5,26	5,97
y	12,49	4,76	2,55	1,60	1,11	0,82	0,63	0,50
Лебедев		x	-0,64	-0,36	-0,08	0,20	0,48	0,76	1,04	1,32
y	29,51	18,86	12,05	7,70	4,92	3,14	2,01	1,28
Лёвочкин		x	-2,45	-1,94	-1,43	-0,92	-0,41	0,10	0,61	1,12
y	0,87	1,19	1,68	2,23	3,04	4,15	5,66	7,72
Матюшанов		x	1,54	1,91	2,28	-2,65	3,02	3,39	3,76	4,13
y	-2,52	-3,08	-3,54	-3,93	-4,27	-4,57	-4,84	-5,09
Мельничук		x	1,20	2,00	2,80	-3,60	4,40	5,20	6,00	6,80
y	-10,84	-6,15	-4,14	-3,02	-2,30	-1,81	-1,45	-1,17
Николаев		x	-1,04	-0,67	-0,30	0,07	0,44	0,81	1,18	1,55
y	10,80	8,08	5,97	4,44	3,31	2,46	1,83	1,36
Носенко		x	0,41	0,97	1,53	-2,09	2,65	3,21	3,77	4,33
y	0,45	1,17	1,56	1,82	2,02	2,18	2,31	2,44
Носиков		x	3,80	0,25	0,48	5,78	4,91	1,56	0,91	5,73
y	-19,23	-21,41	-9,90	-19,56	-0,30	-12,04	1,14	11,26
Овчинников		x
y		7,45	8,24	12,46	13,09	14,56	25,89	29,91
Татьянко		x
y	29,8	22,9	17,1	15,16	10,7	10,2	10,1	25,2
Чурсин		x	1,65	1,39	1,19	1,02	0,82	0,75	0,66	0,89
y	1,034	1,232	1,432	1,752	2,056	2,37	2,76	3,198

 

Лабораторная работа №2. Числовое интегрирование.

Цель работы: ознакомиться с численными методами вычисления определенных квадратов, научиться решать задачи с использованием формул Симпсона, трапеций, правых и левых прямоугольников, метода Монте–Карло и оценивать погрешность всех перечисленных методов.

Исходные данные:

Вычислить приближенное значение интеграла , используя формулы правых и левых прямоугольников, при n=1000.

Формулы правых и левах прямоугольников

Решение:

1. Задаем функцию f(x), отрезок и функцию нахождения дифференциалов n-го порядка.

2. Находим значение интеграла заданной функции для использования его в дальнейшем решении для сравнения.

Составим функцию, входными параметрами которой являются: a, b – левая и правая границы интервала; n – количество разбиений; char – если имеет значение «left», то идет подсчет по формуле левых прямоугольников, любое другое – по формуле правых прямоугольников:

 

Погрешность показывает, что полученное значение интеграла верно до третьего знака после запятой.

Результаты вычисление по формулам правого и левого прямоугольников.

 

Метод Симпсона

Вычислить приближенное значение интеграла , используя общую формулу Симпсона, при n=1000.

 

Решение:

Составим функцию, входными параметрами которой являются: a, b – левая и правая границы интервала; n – количество разбиений. Индексы iEven и iUneven обозначают четность и нечетность.

Следовательно, решением будет число, равное 0,285714286. Погрешность показывает, что полученное значение интеграла верно до девятого знака.

Метод трапеций

Вычислить приближенное значение интеграла , используя формулу трапеций, при n=1000.

 

Решение:

Функция, реализующая вычисление интеграла методом трапеций, имеет вид:

Метод Монте-Карло

Вычислить приближенное значение интеграла , используя метод Монте-Карло, при n=1000 000.

 

Решение:

Метод, реализующий вычисление интеграла методом Монте-Карло, имеет вид:

 

Задание для индивидуального выполнения по вариантам:

	№	f(x)	[a, b]		№	f(x)	[a, b]
Буланов	1.		0; 1	Татьянко	21.		0; 3
Вакуленко	2.		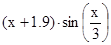1; 2	Чурсин	22.		0,1; 1,1
Воронов	3.		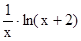2; 3
Вылегжанин	4.		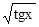0; 0,5
Голованов	5.		1,2; 2,2
Гурнутин	6.		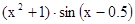0,5; 1,5
Ибрагимов	7.		2; 3
Исенгалиев	8.		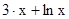1; 2
Кожевников	9.		-0,5; 0,5
Конистратенко	10.		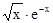0,1; 1,1
Коркин	11.		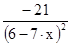-2; 0
Лашманов	12.		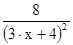0; 1
Лебедев	13.		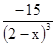3; 5
Лёвочкин	14.		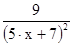2; 3
Матюшанов	15.		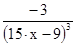-1; 0
Мельничук	16.		0; 3
Николаев	17.		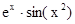0; 5
Носенко	18.		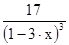-3; -1
Носиков	19.		0; 1
Овчинников	20.		4; 5

 

 

 

Список литературы

1. Поршнев С.В., Численные методы на базе Mathcad / С.В. Поршнев, И.В. Беленкова – СПб.: БХВ-Петербург, 2005. – 464 с.

2. Амосов А.А., Вычислительные методы для инженеров / А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова– М.: Высшая школа, 1994. – 544 с.

3. Самарский А.А., Задачи и упражнения по численным методам: Учебное пособие / А.А. Самарсий, П.И. Ваюищевич, Е.А. Саморская – М.: Эдиториал УРСС, 2000. – 207 с.

 

 

 

Методические указания

 

Алексей Александрович Силаев

Елена Юрьевна Силаева