Тема 1.3. Преобразования простейших выражений.
Теперь перейдем к упрощению логарифмических выражений. Для них нам понадобятся свойства логарифмов, которые мы с Вами уже знаем (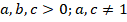
):
1. 
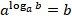
2. 
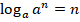
3. 
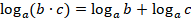
4. 
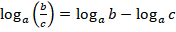
5. 
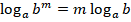
6. 
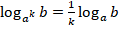
7. 
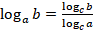
Глядя на формулы, выделим основные моменты, которые нам пригодятся при упрощении выражений, содержащих логарифмы:
для использования формул 3 и 4 выражение под логарифмом нужно представить в виде произведения или частного. Часто эти формулы применяют справа налево; для использования формул 5 и 6 выражение под логарифмом и в основании логарифма нужно представить в виде степени числа; для использования формул сложения, вычитания, деления логарифмов их основания должны быть одинаковы.
Итак, потренируемся упрощать и вычислять значения выражений с логарифмами.
Задание 5. Вычислить:
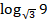
Решение. Выражение под логарифмом и его основание можем представить в виде степени числа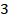 
:
→ 
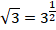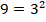
Получаем:
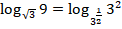
Можем воспользоваться свойствами логарифма:
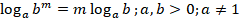
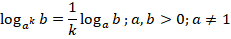
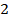выносим как множитель, 
– в знаменатель. Получаем:
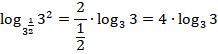
По определению логарифма,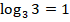 
. В итоге исходное выражение равно 
:
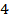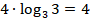
Задание 6. Упростить выражение:
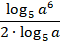
Решение. Видим деление логарифмов с одинаковыми основаниями - можем применить свойство:
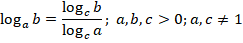
Получаем:
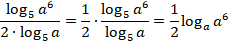
По определению:
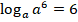
В итоге получаем:
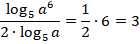
Задание 7. Вычислить:
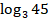
Решение.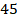 
мы не можем представить в виде степени числа 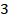. Зато можем разложить на множители:
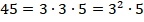
По свойствам логарифмов получаем:
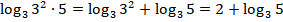
Осталось вычислить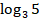 
. Тут уже ничего не упростить, нужно воспользоваться калькулятором. Но в большинстве калькуляторов вы найдете лишь функци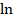и 
и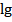 
- натуральные и десятичные логарифмы. Как же, используя их, вычислить 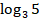? Здесь нам пригодится формула перехода к новому основанию:
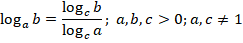
По ней:
Вычисляем на калькуляторе приблизительные значения:
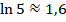
Тогда: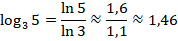 
Исходное выражение:
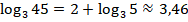
Теперь посмотрим, как можно упрощать логарифмические выражения с использованием эквивалентного определения логарифма – основного логарифмического тождества:
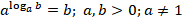
Видим, что для применения формулы нужно, чтобы основание степени и основание логарифма совпадали. Сделать это можно, опять же, представляя выражения в виде степеней.
Задание 8. Вычислить:
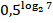
Решение. Основание степени и логарифма отличаются. Для использования основного логарифмического тождества представим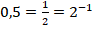 
. Тогда по свойству степеней:
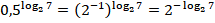
Осталось внести множитель перед логарифмом как степень:
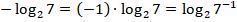
Теперь основания степени и логарифма одинаковы. Можем применить основное логарифмическое тождество:
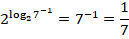
Задание 9. Упростить выражение:
Решение. Здесь уже основание логарифма можем представить в виде степени пятерки:
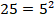
Применяем свойств логарифма:
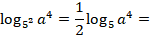
Теперь множитель перед логарифмом можем внести как степень:
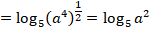
Как и в предыдущем задании, мы получили одинаковые основания степени и логарифма и можем применить основное логарифмическое тождество:
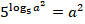
Задание 10. Найдите значения выражений:
а)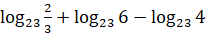 
;
б)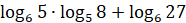 
;
в)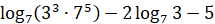 
;
г)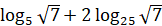 
.
Решение.
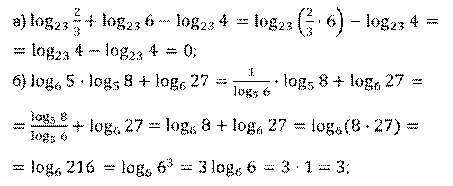
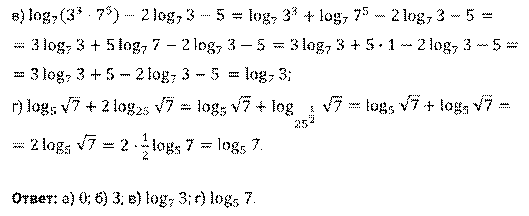
Задание 11. Найдите значения выражений:
а)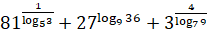 
;
б)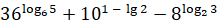 
.
Решение.
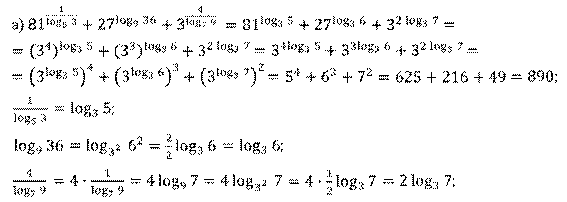
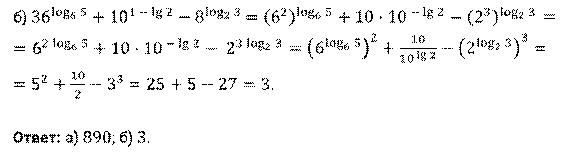
Задание 14. Вычислите: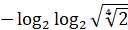 
.
Решение.
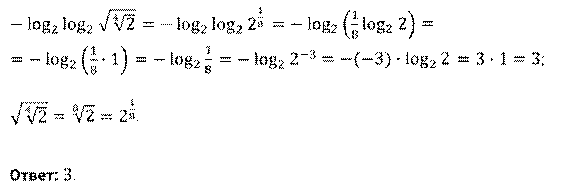
Домашнее задание.
