Теоретические сведения
Основы преобразования Хафа
Пусть задано n точек на изображении (плоскости). Требуется найти подмножество точек, лежащих на некоторых прямых линиях.
Каждая прямая на плоскости описывается уравнением вида:
(1)
Рассмотрим конкретную прямую, на пример:
(2)
и плоскость 
, в которой переменными (координатами) являются параметры уравнения (1), т.е. a и b.
Рис. 1. Образ прямой на плоскости Хафа
Прямая (2) отличается от остальных других прямых двумя параметрами: а0 и b0. От туда можно сказать, что она характеризуется точкой с координатами 
на плоскости 
. Плоскость 
называют плоскостью Хафа, или пространством параметров.
Если теперь рассмотрим конкретную точку (x0,y0) на плоскости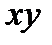 
, то через ее проходят бесконечно много прямых, характеризуемых различными значениями коэффициентов a и b. В этом случае, x0 и y0 являются константами (параметрами уравнения), а a и b - переменными. Преобразуем уравнение (1) в следующий вид:
(3)
На плоскости ab, уравнение (3) соответствует прямой с параметрами x0 и y0.
Следовательно, точка 
, а точнее, семейство прямых, проходящих через точку на плоскости xy, представляет собой прямую (3) на плоскости ab. Это иллюстрируется на рис. 2. Действительно, каждая прямая на плоскости изображения (т.е. плоскости xy) соответствует одной точке на плоскости Хафа, поэтому множество прямых, проходящих через точку , соответствует множеству точек плоскости ab, координаты которых удовлетворяют уравнению прямой с параметрами x0 и y0, т.е. уравнению (3). Такие точки должны находиться на одной и только одной прямой c уравнением (3).
Рис. 2. Образ точки на плоскости Хафа
На рис.3 а) представлены 3 точки A, B, C, находящиеся на одной прямой, описывающейся уравнением (2). Образами этих трех точек на плоскости Хафа являются три прямые:
; 
; 
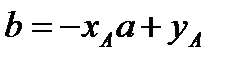(4)
Поскольку три точки A, B, C находятся на прямой (2), их координаты удовлетворяют уравнению (2), т.е.:
; 
; 
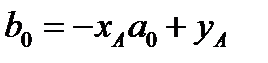(5)
Равенства (5) означают, что три прямые (4) пересекаются в точке 
. Это значит, что образы точек, находящихся на одной прямой, в плоскости Хафа пересекаются в одной точке.
Рис. 3. Образ точек, лежащих на одной прямой в плоскости Хафа
Преобразование Хафа позволяет найти все прямые, проходящие через некоторые множества точек изображения путем определения координат точек пересечения образов этих точек изображения на плоскости Хафа.
Кроме прямых, преобразование Хафа позволяет найти также любые кривые определенной формы на изображении.
Модификация
Рис. 4. Модификация преобразования Хафа
Уравнение прямой вида (1) имеет недостаток, связанный с бесконечным значением параметра 
при стремлении прямой к вертикали. Для устранения данного недостатка используем другую формулу описания прямой, а именно: 
(6),
где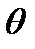 
- угол наклона прямой, 
- расстояние от начала системы координат до прямой (рис. 4). В такой форме представления можем описывать любые прямые на плоскости.
Аналогично разделу 2.1, введем плоскость 
и построим на ней образы точек изображения, находящихся на одной прямой. В результате получается такой же вывод, который получен в разделе 2.1 за исключением того, что образ точки уже не является прямой, а синусоидой.
Алгоритмы реализации преобразования на компьютере
Рис. 5. Дискретизация плоскости Хафа
Привлекательность преобразования Хафа с точки зрения вычислений происходит из возможности разбиения пространства параметров (в данном случае плоскости Хафа) на так называемые ячейки накопления, как показано на рис. 5, где 
и 
- предлагаемые диапазоны значений параметров.
Обычно приняты:
и 
,
где D - расстояние между угловыми точками изображения (максимальное расстояние между началом системы координат и прямой на изображении).
В ячейке с координатами (i,j) накапливается значение A(i,j) для квадрата в пространстве параметров, соответствующего точке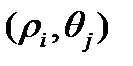 
. Вначале значения всех ячеек накопления равны 0. Затем для каждой точки 
выбранного множества на изображении полагаем параметр 
равным каждому разрешенному дискретному значению 
в ячейках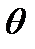 
-оси и находим соответствующее значение 
путем решения уравнения 
. Затем найденные величины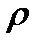 
округляются до ближайшего разрешенного дискретного значения 
. После этого значение соответствующей ячейки накопления увеличивается на единицу: A(i,j)=A(i,j)+1. В конце процедуры значение ячейки A(i,j) равно Q, которое означает, что Q точек плоскости изображения лежат на прямой 
.
Ниже приведен алгоритм реализации преобразования Хафа над изображением размера [M,N].
1. Построить плоскость Хафа вида матрицы h [ nrho, ntheta ], причем:
ntheta =size( theta ), theta - вектор значений параметра 
, начиная с -90 град. до +90 град. с шагом dtheta.
nrho =size(rho), rho - вектор значений параметра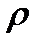 
, начиная с -D до +D c шагом drho.
.
В начале все элементы матрицы h равны 0.
2. Найти координаты всех точек изображения, яркость которых отличается от нуля. Пусть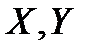 
- векторы размера k, содержащие координаты всех ненулевых элементов изображения.
3. Цикл i=1:k
Цикл j=1: ntheta
1. Найти 
по формуле: 
2. Округлять 
3. Увеличить значение ячейки накопления на единицу: 