Цель работы
Изучение правил программирования программ циклической структуры с предусловием и методов нахождения корней нелинейных и трансцендентных уравнений.
Общие сведения
Во многих алгоритмах число повторений цикла заранее неизвестно. Для таких алгоритмов язык Си предоставляет реализации циклов с предусловием и постусловием. В этих видах циклов проверка условия продолжения цикла осуществляется соответственно до и после выполнения тела цикла.
Синтаксис цикла с предусловием:
while (выражение)
оператор [блок операторов];
Проверка условия продолжения цикла осуществляется до выполнения тела цикла. Пока результат выражения не равен нулю, выполняется оператор (блок операторов). Перед входом в цикл while первый раз инициализируется одна или несколько переменных для того, чтобы условное выражение имело какое-то значение. Если выражение равно нулю, то тело цикла не выполняется ни разу. Если выражение не равно нулю - выполняется тело цикла.
Оператор в теле цикла должен изменять переменную (переменные) цикла, для того чтобы выражение в конце концов обратилось в нуль и цикл завершился.
Для цикла while, как и для других видов циклов, характерны типичные ошибки, приводящие к зацикливанию. Пример такой ошибки:
i = 0;
while (i < 10);
i + = 2
В этом случае следует помнить, что точка с запятой представляет собой ‘ пустой’ оператор, который будет выполняться бесконечно, а оператор модификации переменной цикла i + = 2; не выполняется.
Другой распространенной ошибкой является использование в условном выражении вместо операции отношения = = операции присваивания =. Например:
while (i = 2)
< блок операторов >.
В этом случае условное выражение всегда дает результат, отличный от нуля, что также приводит к зацикливанию. Закончить выполнение цикла while можно при обращении в нуль выражения, либо используя в теле цикла операторы break и return.
|
|
Цикл while можно использовать для контроля каких-либо действий пользователя, например, ввода данных:
int i = 0
while (i < 0 || i >= 100)
{ puts (²Введите число в диапазоне от 1 до 99²);
scan f (² %d ²,&i);}
В этом случае если введенное число не попадает в заданный диапазон, ввод будет повторяться, не пропуская неверные данные для дальнейшей обработки.
Нахождение корней уравнений
Нахождение корней уравнений F(x) = 0 рассматриваемыми методами осуществляется в два этапа: отделение и уточнение корней.
На первом этапе производится нахождение диапазонов, в каждом из которых находится только один корень. Реализация этого этапа может быть приведена графически или табулированием функции. При табулировании в качестве границ диапазона следует выбирать значения аргумента, соответствующие соседним значениям функции, имеющим разные знаки. Второй этап - уточнение корней, т.е. нахождение их значений с необходимой погрешностью, может производиться разными методами. В данной работе рассматриваются простейшие из них: метод половинного деления (дихотомии) и метод Ньютона.
Метод половинного деления
Состоит в последовательном делении отрезка (a, b), в котором находится только один корень, пополам: x = (a + b)/2.
После этого находят значение функции F(x) и сравнивают его знак со знаком функции на левой границе интервала F(a). Если знаки совпадают (F(a)×F(x) > 0), корня в диапазоне a, x нет и левая граница сдвигается до значения a = x. Если знаки не совпадают (F(a)×F(x) < 0), корень находится в диапазоне a, x, диапазон x, b - пустой. В этом случае сдвигается правая граница диапазона b = x. Процесс сужения диапазона продолжается до достижения необходимой для данной физической задачи погрешности.
|
|
|F(x)| < E. Блок-схема алгоритма уточнения корня уравнения F(x) = 0 методом дихотомии показана на рис. 1. Достоинства данного метода: простота реализации и гарантированная сходимость. Недостаток - медленная по сравнению с другими методами сходимость 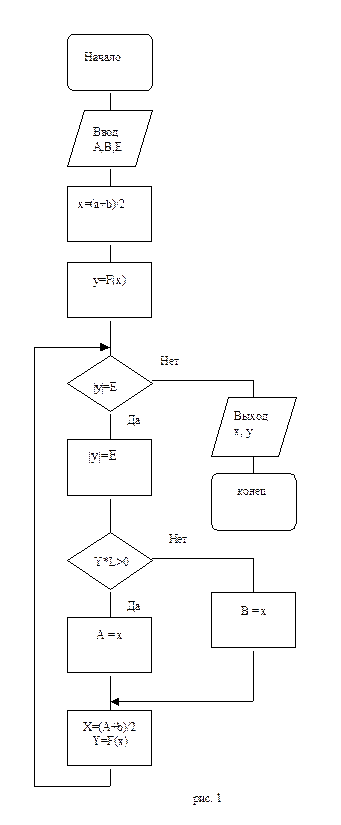
Метод Ньютона
Метод Ньютона (касательных) основан на нахождении очередного приближения  , как точки пересечения касательной в точке
, как точки пересечения касательной в точке  и оси абсцисс. Итерационный процесс схождения к корню реализуется формулой:
и оси абсцисс. Итерационный процесс схождения к корню реализуется формулой:
 где
где  - первая производная функции F(x), блок-схема алгоритма реализующего метод касательных показана на рис. 2.
- первая производная функции F(x), блок-схема алгоритма реализующего метод касательных показана на рис. 2. 
В качестве x0 выбирают тот конец отрезка a, b, на котором знаки функции F(x) и ее второй производной F’’(x) совпадают (F(x)×F’’(x) > 0). В этом случае обеспечивается наиболее быстрая (квадратичная) сходимость.
Контрольные вопросы
Нарисуйте блок-схему циклического вычислительного процесса с предусловием.
Какое минимальное число раз может выполняться цикл while?
В чем сущность уточнения корней методом половинного деления?
Как подсчитать количество итераций при уточнении корней?
Какое минимальное значение может иметь погрешность уточнения корня для типа float?
Покажите графически, в чем состоит принцип уточнения корней методом Ньютона?
|
|
Что неправильно в приведенном цикле?
while (i <=S || S > i)
операторы;
Варианты заданий
1-6. Вычислить значение интеграла I с погрешностью E < 10-3 по формуле трапеций:

где f(x) - подынтегральная функция, a и b - соответственно нижний и верхний пределы интегрирования, h = (b - a)/n,  .
.
1. 
2. 
3. 
4. 
5. 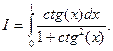
6. 
7-13. Уточнить корни уравнения в заданном диапазоне с погрешностью E < 10-3 методом Ньютона:
 .
.
7.3sin(x) + 0.35x - 3.8 = 0 2< x < 3.
8.  0 < x < 1.
0 < x < 1.
9.  0 < x < 1.
0 < x < 1.
10. x - 2 + sin(1/x) = 0 1.2 < x < 2.
11. 1 - x + sin(x) - ln(1 + x) = 0 0 < x < 15.
12. x2 - ln(1+x) - 3 = 0 2 < x < 3.
13. ln(x) - x + 1.8 = 0 2 < x < 3.
14-21. Найти корни уравнения с погрешностью E < 10-4 методом половинного деления:
14.  .
.
15. 3x/1.6 - 2.3x - 3 = 0.
16. tg(x) - tg3(x)/3 + tg5(x)/5 = 0.
17. cos(2/x) - 2sin(1/x) + 1/x = 0.
18.  .
.
19.  .
.
20. sin(x2) + cos(x2) - 10x = 0.
21. x2 - cos(2x) - 1 = 0.
Лабораторная работа № 6