Цель работы
Изучение приемов программирования сложных циклических процессов.
Методические указания
Как известно, любой циклический вычислительный процесс состоит из следующих частей:
- блока подготовки, в котором инициализируются начальные значения переменных, прежде всего параметра цикла;
- тела цикла, состоящего из операторов, которые выполняются до тех пор, пока выполняется условие продолжения цикла;
- блока или части, содержащей условие продолжения (окончания) циклического процесса.
Если телом цикла является циклическая структура, то такие циклы называются вложенными или сложными циклическими процессами.
Циклическая структура, содержащая в себе другую циклическую структуру, называется внешним циклом. А цикл, содержащийся внутри другого, называется внутренним.
Внутренний и внешний циклы могут быть любыми из трех рассмотренных выше типов: со счетчиком, с предусловием, с постусловием.
Правила организации как внешнего, так и внутреннего цикла такие же, как и для простых циклов, рассмотренных выше видов. Однако нужно выполнить следующее условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла.
Кроме того, нужно помнить, что при передаче управления от внешнего цикла к внутреннему, необходимо восстановить начальное значение параметра внутреннего цикла. В качестве примера рассмотрим фрагмент программы, который вычисляет значение функции двух переменных z = f(x, y), если аргумент x меняется от x0 до xN с шагом  , а аргумент y меняется от y0 до
, а аргумент y меняется от y0 до  . Блок-схема подобного вычислительного процесса представлена ниже.
. Блок-схема подобного вычислительного процесса представлена ниже.
 |
Блоки 3, 4, 5 составляют внутренний цикл с параметром x, внешний цикл
|
|
имеет параметр y и содержит блоки 2, 3, 4, 5, 6, 7. Ниже представлены варианты реализации представленного на рисунке двойного вложенного цикла.
Первый фрагмент программы использует оператор for и имеет вид:
..........
for (y0; y <= yM; y+ = hy)
{ printf (² y = %d², y);
for (x0; x <= xN; x + = hx)
{ z = F(x, y);
printf (²x = %d _ _z = %d \n², x, z);
}
}
Второй вариант той же самой программы использует оператор do-while и имеет вид:
y = y0;
do
{ x = x0;
printf (²y = %d², y);
do
{ z = F(x, y); printf (²x = %d_z = %d \n², x, z);
x = x + hx;
}
while x £ xN;
y = y + hx;
}
while y £ xM;
Аналогично будет выглядеть вариант с использованием оператора while.
Пример выполнения задания
Вычислить значение интеграла  методом трапеций для различных значений верхнего предела а, если он меняется от
методом трапеций для различных значений верхнего предела а, если он меняется от  с шагом
с шагом  . Число точек разбиения интервала задано и равно n = 46. Для каждого вычисленного значения оценить абсолютную погрешность как разность между приближенным значением интеграла и точным, которая подсчитывается по первообразной интеграла.
. Число точек разбиения интервала задано и равно n = 46. Для каждого вычисленного значения оценить абсолютную погрешность как разность между приближенным значением интеграла и точным, которая подсчитывается по первообразной интеграла.
Первообразная данного интеграла имеет вид:  . Решение:
. Решение:
Формула трапеций для вычисления интеграла  имеет вид
имеет вид  или, в другом виде
или, в другом виде  где yk = yi - значение подынтегральной функции в точке xk = xk-1 + h, где шаг
где yk = yi - значение подынтегральной функции в точке xk = xk-1 + h, где шаг  . В программе можно использовать как первую, так и вторую функции.
. В программе можно использовать как первую, так и вторую функции.
Программа представляет сложный циклический процесс, в котором внешний цикл обеспечивает изменение верхнего предела интегрирования а с шагом  в данном диапазоне, а внутренний цикл по переменной x обеспечивает вычисление интеграла при фиксированном значении а методом трапеций.
в данном диапазоне, а внутренний цикл по переменной x обеспечивает вычисление интеграла при фиксированном значении а методом трапеций.
Необходимые пояснения к программе представлены в виде комментариев. Текст программы приведен ниже.
|
|
/* пример вычисления интеграла */
main ()
{ float a, a0,aN, ha, x, x0, xN, hx, Jnt;
int n;
/* введем данные a0, aN, ha */
scanf (²%f %f %f², &a0, &aN, &ha);
/* введем данные n */
scanf (²%i ², &n);
/*введем нижний предел интегрирования x0 */
scanf (²%f ², &x0);
/* начало цикла по а - верхнему пределу */
for (a = a0; a <= aN; a + = ha)
{ /* печатаем текущий верхний предел интегрирования */
printf (²a = %f \n², a);
/* вычисляем интеграл при заданном а */
Jnt = 0; hx = (a - x0)/n;
for (x0; x <= a; x+ = h;
{
Jnt = Jnt + exp(-2*x);
}
Jnt = h*Jnt + h(exp(-2*x-) + exp(-2*a)/2;
/* печатаем а и значение Jnt */
printf (²a = %d_ _Jnt = %d², a, Jnt
}
вставить оценку погрешности
}.
При выполнении варианта задания, в котором нужно найти корни уравнения f(x) = 0 при различных параметрах, прежде всего нужно представить уравнение в виде x = F(x), где |F’(x)| < 1. Это обеспечивает сходимость итерационного процесса.
Контрольные вопросы
Дайте определение сложного циклического процесса.
Нарисуйте блок-схему вложенных циклов для циклических процессов со счетчиком, с постусловием и предусловием.
Какие условия нужно выполнять при написании программ, содержащих вложенные циклы?
Что изменится, если поменять местами внутренний и внешний циклы?
Варианты заданий
 N варианта N варианта
| Уравнение | Диапазон изменения параметра А | 
| Начальное приближение |

| 0.2<A<0.4 | 00.01 | 2.2985 | |

| 2£A£2.5 | 00.1 | 0.2561 | |
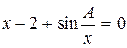
| 0.5£A£1 | 00.1 | 1.3077 | |

| 0.25£A£0.55 | 00.05 | 0.9800 | |

| 1£A£2 | 00.1 | 2.0297 |
В заданиях с номером 7 и выше вычислить значения интеграла  методом трапеций, если один из пределов интегрирования a или b меняется в заданном диапазоне с некоторым шагом. Для каждого значения параметра вычислить абсолютную погрешность как разность между приближенным и точным значением интеграла, вычисленным по первообразной этого интеграла. Исходные данные для выполнения задания приведены в таблице.
методом трапеций, если один из пределов интегрирования a или b меняется в заданном диапазоне с некоторым шагом. Для каждого значения параметра вычислить абсолютную погрешность как разность между приближенным и точным значением интеграла, вычисленным по первообразной этого интеграла. Исходные данные для выполнения задания приведены в таблице.
|
|
| N вариан-та | Подынтегра-льная функция f(x) | Пределы интегриро-вания | Коли-чество точек разбие-ния | Первообразная функция |
| excos2x | a = 0


| n = 60 | 
|
Окончание табл.
| N варианта | Подынтегра-льная функция f(x) | Пределы интегриро-вания | Количество точек разбиения | Первообразная функция |
| (xlnx)2 | b = e
e = 2,71..
0.5£a£1.5

| n = 52 | 
| |

| a = 0


| n = 40 | 
| |

| a = 0


| n = 36 | 
| |

| a = 0


| n = 150 | 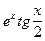
| |

| a = 0


| n = 78 | 
| |

| a = 0


| n = 150 | 
| |

| a = 0
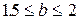

| n = 50 | 
| |

| a = 0


| n = 150 | 
|
16.Составить программу вычисления значений функции f(a, b), если а меняется от  до
до  с шагом
с шагом  , а
, а  . Все данные вводятся с клавиатуры. Функция
. Все данные вводятся с клавиатуры. Функция 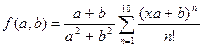 , где
, где 


17.Составить программу вычисления значений функции f(a, b), если а меняется от  до
до  с шагом
с шагом  , а
, а  . Все данные вводятся с клавиатуры. Вычислить таблицу значений функции
. Все данные вводятся с клавиатуры. Вычислить таблицу значений функции  , при
, при

18.Вычислить таблицу значений функции  , где
, где  и
и  , а
, а

19.Вычислить таблицу значений функции  , где
, где
y = 0.1 (0.1) 1.5,
x = 5 (0.2) 6,
b – вводится,
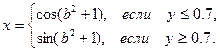
20.Вычислить таблицу значений функции
 , где
, где 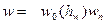 и
и  . Все параметры выбираются произвольно и вводятся с клавиатуры.
. Все параметры выбираются произвольно и вводятся с клавиатуры.
Лабораторная работа № 7