2.4.1 Метод Циклического покоординатного спуска
В данном методе на каждой итерации выполняется n(количество координат) одномерных минимизаций (спусков) вдоль единичных орт. Этот метод работает особенно хорошо, если линии равного уровня расположены вдоль координатный осей.
Начальный этап:
Выбрать x1, e, k=1, l=1.
Основной этап:
Шаг 1
1) В качестве направления p выбрать 
, где ненулевая позиция имеет индекс l.
2) Найти L как результат минимизации функции по направлению p.
3) 
4) Если l<n то Шаг 2, иначе повторить Шаг 1 с l = l+1.
Шаг 2
1) Вычислить 
2) Проверить КОП: если 
, то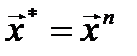 
, иначе 
, l=1 и на Шаг1.[7]
2.4.2 Метод Гаусса-Зейделя
Начальный этап:
Выбрать х1, ε = 10-4 – 10-8 установить k = 1;
Основной этап:
Шаг 1.
Выполнить серию одномерных поисков вдоль координатных орт:
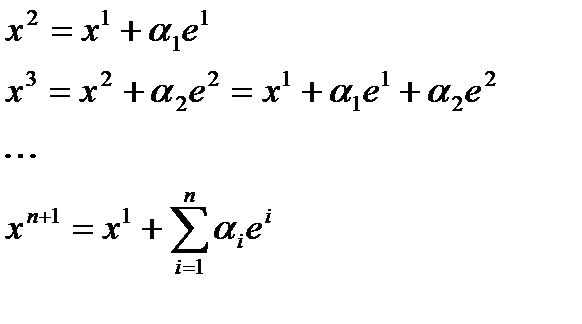
Шаг 2.
Вычислить ускоряющее направление и проверить КОП: 
, если выполняется, минимум найден: x*=xn+1.
Иначе:
· Выполнить ускоряющий шаг в новую точку хn+2
· Обозначить последнюю точку как начальную и вернуться на шаг 1.[7]
2.4.3 Метод параллельных касательных
Начальный этап:
Выбрать х1, ε = 10-4 – 10-8 установить k = 1;
Основной этап:
Шаг 1.
Из точки x1 выполнить антиградиентный в точку x2= x1+α1р1, где p1=-Ñу1.
Шаг 2.
Последовательно выполнить две операции:
1)Антиградиентный спуск в точку x3.
Вычислить ускоряющее направление d=x3-x1 и, не останавливаясь совершить ускоряющий шаг в точку x4=x3+α3d.
Шаг 3.
2)Проверить КОП: 
- остановиться x*=x4.
Иначе:
3)Обозначить x2 как новую начальную x1=x2, а точку x4 как новую точку ускорения x2=x4.
Перейти к шагу 2.[7]
2.4.4 Градиентные методы
Основная идея методов заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом 
:
|
|
,
где 
выбирается:
· постоянной, в этом случае метод может расходиться;
· дробным шагом, то есть длина шага в процессе спуска делится на некое число;
· наискорейшим спуском: 
.[7]
Метод наискорейшего спуска (метод градиента)
Выбирают 
, где все производные вычисляются при 
, и уменьшают длину шага по мере приближения к минимуму функции 
.
Для аналитических функций и малых значений 
тейлоровское разложение 
позволяет выбрать оптимальную величину шага:
,
где все производные вычисляются при . Параболическая интерполяция функции может оказаться более удобной.
Алгоритм
1)Задаются начальное приближение и точность расчёта 
2)Рассчитывают , где
3)Проверяют условие останова:
Если 
, то 
и переход к шагу 2.
Иначе 
и останов.[7]
Метод сопряженных градиентов
Рассмотренные выше градиентные методы отыскивают точку минимума функции в общем случае лишь за бесконечное число итераций. Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость их сходимости и позволяет, например, минимизировать квадратичную функцию:
f(x) = (х, Нх) + (b, х) + а
с симметрической положительно определенной матрицей Н за конечное число шагов п, равное числу переменных функции. Любая гладкая функция в окрестности точки минимума хорошо аппроксимируется квадратичной, поэтому методы сопряженных градиентов успешно применяют для минимизации и неквадратичных функций. В таком случае они перестают быть конечными и становятся итеративными. По определению, два n-мерных вектора х и у называют сопряженными по отношению к матрице H (или H-сопряженными), если скалярное произведение (x, Ну) = 0. Здесь Н - симметрическая положительно определенная матрица размером пхп.
|
|
Одной из наиболее существенных проблем в методах сопряженных градиентов является проблема эффективного построения направлений. Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шаге антиградиента -f(x[k]) в направление p[k], H-сопряженное с ранее найденными направлениями р[0], р[1],..., р[k-1]. Рассмотрим сначала этот метод применительно к задаче минимизации квадратичной функции.
Направления р[k] вычисляют по формулам:
p[k] = -f’(x[k])+bk-1p[k-l], k >= 1;
p[0] = -f’(x[0]).
Величины bk-1 выбираются так, чтобы направления p[k], р[k-1] были H-сопряженными:
(p[k], Hp[k-1])= 0.
В результате для квадратичной функции
,
итерационный процесс минимизации имеет вид:
x[k+l] =x[k] +akp[k],
где р[k] - направление спуска на k-м шаге; аk - величина шага. Последняя выбирается из условия минимума функции f(х) по а в направлении движения, т. е. в результате решения задачи одномерной минимизации:
f(х[k] + аkр[k]) = 
f(x[k] + ар [k]).
Для квадратичной функции
Алгоритм метода сопряженных градиентов Флетчера-Ривса состоит в следующем.
1. В точке х[0] вычисляется p[0] = -f’(x[0]).
2. На k-м шаге по приведенным выше формулам определяются шаг аk. и точка х[k+1].
3. Вычисляются величины f(x[k+1]) и f’(x[k+1]).
4. Если f’(x[k+1]) = 0, то точка х[k+1] является точкой минимума функции f(х). В противном случае определяется новое направление p[k+l] из соотношения:
и осуществляется переход к следующей итерации. Эта процедура найдет минимум квадратичной функции не более чем за п шагов. При минимизации неквадратичных функций метод Флетчера-Ривса из конечного становится итеративным. В таком случае после (п+1)-й итерации процедуры 1-4 циклически повторяются с заменой х[0] на х[п+1], а вычисления заканчиваются при 
, где 
- заданное число. При этом применяют следующую модификацию метода:
|
|
x[k+l] = x[k] +akp[k],
p[k] = -f’(x[k])+bk-1p[k-l], k >= 1;
p[0] = -f’(x[0]);
f(х[k] + akp[k]) = f(x[k] + ap[k];
.
Здесь I- множество индексов: I = {0, n, 2п, Зп,...}, т. е. обновление метода происходит через каждые пшагов.
Геометрический смысл метода сопряженных градиентов состоит в следующем (Рисунок 1). Из заданной начальной точки х[0] осуществляется спуск в направлении р[0] = -f'(x[0]). В точке х[1] определяется вектор-градиент f'(x [1]). Поскольку х[1] является точкой минимума функции в направлении р[0], то f’(х[1])ортогонален вектору р[0]. Затем отыскивается вектор р [1], H-сопряженный к р [0]. Далее отыскивается минимум функции вдоль направления р[1] и т. д.[7]
Рисунок 1. Траектория спуска в методе сопряженных градиентов
Рисунок 2. Поиск экстремума квадратичной функции методом покоординатного спуска (а), методом параллельных касательных (б), методом наискорейшего спуска (в) и методом сопряженных градиентов (г).
Заключение
Для успешного функционирования промышленных предприятий в современных условиях абсолютно необходимы передовые информационные технологий. Они позволяют не только решать широкий круг задач в сфере автоматизации финансово-хозяйственной и управленческой деятельности, но и осуществлять комплексную автоматизацию основных технологических и производственных бизнес-процессов.
На сегодняшний день внедрение САПР в производство предприятие является не таким уж и трудоемким, как на первый взгляд. Многие готовые системы САПР выпускаются сейчас, и их стоимость чуть выше 500$, в зависимости от рабочих мест. Конечно, есть бесплатные, которые можно закачать с интернета. Но от них никакой технической поддержке. И еще неизвестно как они себя поведут.
Независимо от того какая система САПР необходима:
- PDM система - Управления данными об изделиях (Product Data
Management);
- PLM система - Управления жизненным циклом изделия (Product
Lifecycle Management);
- TDM система - Ведения электронного архива технической
документации (Technical Data Management);
необходимо хорошо развитая локальная сеть и компьютер с большим объемом памяти жесткого диска, для базы данных всей документации. И конечно же желание руководства.
Список источников
1. Малюх, В. Н. Введение в современные САПР: Курс лекций/В. Н. Малюх — М.: ДМК Пресс, 2010. — 192 с.
2. Норенков, И. П. Основы автоматизированного проектирования: учеб. для вузов. — 4-е изд., перераб. и доп./ И. П. Норенков — М.: Изд-во МГТУ им. Н. Э. Баумана, 2009. — 430 с.
3. Норенков, И. П. Автоматизированное проектирование. Учебник / И. П. Норенков — М.: Изд-во МГТУ им. Н. Э. Баумана, 2000. — 188 с.
4. Петров, А. В. Проблемы и принципы создание САПР/ А. В. Петров. — Москва: 1990г. — 130 с.
5. Жук, Д. М. Технические средства и операционные системы САПР/ Д. М. Жук. — Москва: 1986 г. — 59 с.
6. Фролов, В.А. Анализ и оптимизация в прикладных задачах конструирования/ В.А. Фролов — М.: Высшая школа, 1976. — 101 с.
7. Стронгин, Р.Г. Численные методы в многоэкстремальных задачах (информационно-статистические алгоритмы)/ Р.Г. Стронгин // Серия: "Оптимизация и исследование операций".— М.: Изд-во "Наука", 1978. — 215 с.
8. Курицкий, Б.Я. Оптимизация вокруг нас/ Б.Я. Курицкий: Машиностроение, 1989. —144с.