 В магазине имеется 6 сортов шоколадных конфет и 4 сорта карамели. Сколько различных покупок конфет одного сорта можно сделать в этом магазине? Сколько можно сделать различных покупок, содержащих один сорт шоколадных конфет и один сорт карамели?
В магазине имеется 6 сортов шоколадных конфет и 4 сорта карамели. Сколько различных покупок конфет одного сорта можно сделать в этом магазине? Сколько можно сделать различных покупок, содержащих один сорт шоколадных конфет и один сорт карамели?
Ответ: 10 и 24.
 В отряде 5 разведчиков, 4 связиста и 2 санитара. Сколькими способами можно выбрать одного солдата так, чтобы он был разведчиком или санитаром? Сколькими способами можно составить разведгруппу из трех человек, чтобы в нее вошли разведчик, связист и санитар?
В отряде 5 разведчиков, 4 связиста и 2 санитара. Сколькими способами можно выбрать одного солдата так, чтобы он был разведчиком или санитаром? Сколькими способами можно составить разведгруппу из трех человек, чтобы в нее вошли разведчик, связист и санитар?
Ответ: 7 и 40.
 В букинистическом магазине продаются 6 экземпляров романа И.С. Тургенева «Рудин», 3 экземпляра романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, имеется 5 томов, состоящих из романов «Рудин» и «Дворянское гнездо», и 7 томов, состоящих из романов «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
В букинистическом магазине продаются 6 экземпляров романа И.С. Тургенева «Рудин», 3 экземпляра романа «Дворянское гнездо» и 4 экземпляра романа «Отцы и дети». Кроме того, имеется 5 томов, состоящих из романов «Рудин» и «Дворянское гнездо», и 7 томов, состоящих из романов «Дворянское гнездо» и «Отцы и дети». Сколькими способами можно сделать покупку, содержащую по одному экземпляру каждого из этих романов?
Ответ: 134.
 В цветочном городе решили провести выборы мэра, заместителя мэра и начальника полиции. Сколько различных вариантов исходов выборов может произойти, если в городе живет 100 коротышек?
В цветочном городе решили провести выборы мэра, заместителя мэра и начальника полиции. Сколько различных вариантов исходов выборов может произойти, если в городе живет 100 коротышек?
Ответ: 970 200.
 Даны цифры от 1 до 9. Называется случайное четырехзначное число, состоящее из этих цифр. Найти вероятность того, что оно нечетное, если: а) цифры не повторяются; б) повторяются.
Даны цифры от 1 до 9. Называется случайное четырехзначное число, состоящее из этих цифр. Найти вероятность того, что оно нечетное, если: а) цифры не повторяются; б) повторяются.
Ответ: в обоих случаях 5/9.
 Из колоды (36 карт) вынимают две. Какова вероятность того, что они одной масти?
Из колоды (36 карт) вынимают две. Какова вероятность того, что они одной масти?
Ответ: 8/35.
 На карточках написаны отдельные буквы слова «пилот». Какова вероятность того, что при их случайном раскладе выпадет это слово.
На карточках написаны отдельные буквы слова «пилот». Какова вероятность того, что при их случайном раскладе выпадет это слово.
Ответ: 1/120.
 Агрохимик проверяет 6 типов минеральных удобрений; ему нужно провести несколько опытов по изучению совместного влияния любой тройки удобрений. Для каждого опыта берется участок 0,25 гектар. На какой площади проводится все исследование?
Агрохимик проверяет 6 типов минеральных удобрений; ему нужно провести несколько опытов по изучению совместного влияния любой тройки удобрений. Для каждого опыта берется участок 0,25 гектар. На какой площади проводится все исследование?
Ответ: 5 гектар.
 25 выпускников школы решили обменяться фотокарточками. Сколько было всего заказано фотокарточек?
25 выпускников школы решили обменяться фотокарточками. Сколько было всего заказано фотокарточек?
Ответ: 600.
Алгебра событий
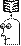 Суммой двух событий А и В называется событие С, состоящее в том, что наступит или событие А, или событие В, или оба вместе:
Суммой двух событий А и В называется событие С, состоящее в том, что наступит или событие А, или событие В, или оба вместе: 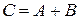 .
.
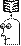 Суммой нескольких событий называется событие, состоящее в том, что наступит хотя бы одно из них.
Суммой нескольких событий называется событие, состоящее в том, что наступит хотя бы одно из них.
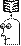 Произведением двух событий А и В называется событие С, состоящее в том, что наступит и событие А, и событие В:
Произведением двух событий А и В называется событие С, состоящее в том, что наступит и событие А, и событие В: 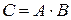 .
.
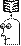 Произведением нескольких событий называется событие, состоящее в том, что наступят все эти события.
Произведением нескольких событий называется событие, состоящее в том, что наступят все эти события.
Рассмотрим основные свойства сумм и произведений событий:
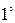 . Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий: 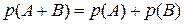 .
.
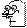 Пример 6.3.1. Какова вероятность того, что Ваш день рождения придется на выходной день.
Пример 6.3.1. Какова вероятность того, что Ваш день рождения придется на выходной день.
Вероятность того, что день рождения придется на субботу, равна 1/7. Аналогичный вывод можно сделать и для воскресенья. Таким образом, вероятность того, что день рождения придется на выходной день, равна  .
.
 . Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
. Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:  .
.
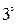 . Сумма вероятностей попарно несовместных событий, образующих полную группу, равна 1.
. Сумма вероятностей попарно несовместных событий, образующих полную группу, равна 1.
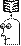 Противоположными называются два единственно возможных события, образующих полную группу. Если прямое событие обозначают за А и вероятность его появления р, то противоположное ему событие обозначают
Противоположными называются два единственно возможных события, образующих полную группу. Если прямое событие обозначают за А и вероятность его появления р, то противоположное ему событие обозначают  , а его вероятность q.
, а его вероятность q.
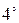 . Вероятность противоположного события вычисляется по формуле:
. Вероятность противоположного события вычисляется по формуле: 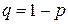 .
.
 Если наступление некоторого события не связано с каким-то другим событием, то в этом случае имеет место безусловная вероятность. В противоположном случае, когда значение вероятности события А каким-либо образом зависит от события В, имеет место условная вероятность. Обозначается условная вероятность
Если наступление некоторого события не связано с каким-то другим событием, то в этом случае имеет место безусловная вероятность. В противоположном случае, когда значение вероятности события А каким-либо образом зависит от события В, имеет место условная вероятность. Обозначается условная вероятность 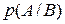 и означает «условная вероятность события А при условии, что событие В уже наступило».
и означает «условная вероятность события А при условии, что событие В уже наступило».
 . Вероятность совместного появления двух событий равно произведению условной вероятности одного из них на безусловную вероятность другого:
. Вероятность совместного появления двух событий равно произведению условной вероятности одного из них на безусловную вероятность другого: 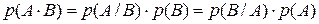 .
.
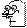 Пример 6.3.2. Ученик извлекает 2 раза по одному билету из 34. Какова вероятность того, что ученик сдаст экзамен, если выучил 30 билетов, а первый билет вытащил неудачно?
Пример 6.3.2. Ученик извлекает 2 раза по одному билету из 34. Какова вероятность того, что ученик сдаст экзамен, если выучил 30 билетов, а первый билет вытащил неудачно?
Пусть событие А – ученик вытащил первый билет неудачно, а событие В – удачно. При этом событие В / А – ученик вытащил второй билет удачно, но первый билет – неудачно; Тогда необходимо найти вероятность события 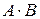 . Используя свойство
. Используя свойство  , можно утверждать, что
, можно утверждать, что
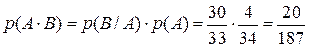 .
.
 Независимыми называется события, когда вероятность появления одного из них не изменяет вероятности появления другого. Для независимых событий условная вероятность равна его безусловной вероятности.
Независимыми называется события, когда вероятность появления одного из них не изменяет вероятности появления другого. Для независимых событий условная вероятность равна его безусловной вероятности.
 . Для двух независимых событий вероятность их совместного появления равна произведению их вероятностей:
. Для двух независимых событий вероятность их совместного появления равна произведению их вероятностей: 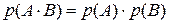 .
.
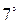 . Вероятность совместного появления несколько взаимно независимых событий равна произведению их вероятностей:
. Вероятность совместного появления несколько взаимно независимых событий равна произведению их вероятностей:  .
.
 Пример 6.3.3. На улице опросили троих случайных прохожих. Какова вероятность, что хотя бы двое из них родились в понедельник?
Пример 6.3.3. На улице опросили троих случайных прохожих. Какова вероятность, что хотя бы двое из них родились в понедельник?
Обозначим за событие А – первый прохожий родился в понедельник, В – второй, С – третий, D – хотя бы двое из троих. Очевидно, что 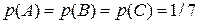 , а
, а  . Искомое событие можно представить в виде суммы несовместных слагаемых
. Искомое событие можно представить в виде суммы несовместных слагаемых 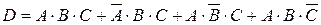 . События А, В, С – независимые друг от друга, поэтому справедливо, что
. События А, В, С – независимые друг от друга, поэтому справедливо, что

 . Вероятность появления хотя бы одного из нескольких взаимно независимых событий равна разности между 1 и произведением вероятностей противоположных событий:
. Вероятность появления хотя бы одного из нескольких взаимно независимых событий равна разности между 1 и произведением вероятностей противоположных событий: 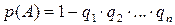 .
.
 . Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:  .
.
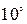 . Предположим, что событие А может наступить только совместно с одним из несколько взаимно несовместных событий
. Предположим, что событие А может наступить только совместно с одним из несколько взаимно несовместных событий 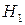 ,
,  , …,
, …, 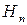 , называемых гипотезами. Тогда справедлива формула полной вероятности
, называемых гипотезами. Тогда справедлива формула полной вероятности

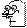 Пример 6.3.4. Имеются три коробки: в первой – 5 белых и 3 черных шара, во второй – 4 белых и 4 черных, в третьей – 8 белых. Наугад выбирается коробка и из нее наугад выбирается шар. Какова вероятность того, что он окажется черным.
Пример 6.3.4. Имеются три коробки: в первой – 5 белых и 3 черных шара, во второй – 4 белых и 4 черных, в третьей – 8 белых. Наугад выбирается коробка и из нее наугад выбирается шар. Какова вероятность того, что он окажется черным.
Обозначим за 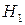 – шар будет извлечен из первой коробки,
– шар будет извлечен из первой коробки,  – из второй,
– из второй, 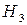 – из третьей. Очевидно, что
– из третьей. Очевидно, что 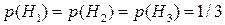 . Тогда
. Тогда  – черный шар будет извлечен из первой коробки (
– черный шар будет извлечен из первой коробки (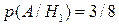 ),
),  – из второй (
– из второй ( ),
),  – из третьей (
– из третьей (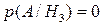 ). Тогда вероятность события А – извлечения черного шара – будет равна
). Тогда вероятность события А – извлечения черного шара – будет равна 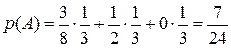 .
.
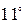 . В этих же условиях справедлива формула Байеса: предположим, что событие А уже наступило и требуется найти условную вероятность гипотезы, которая при этом имела место, тогда
. В этих же условиях справедлива формула Байеса: предположим, что событие А уже наступило и требуется найти условную вероятность гипотезы, которая при этом имела место, тогда 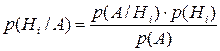 .
.
 Пример 6.3.5. На фабрике 30% продукции производится первым цехом, 25% – вторым и 45 – третьим. Брак в первом цехе 1%, во втором – 1,5%, в третьем – 2%. Наугад выбранная продукция оказалась браком. Какова вероятность того, что она была произведена первым цехом.
Пример 6.3.5. На фабрике 30% продукции производится первым цехом, 25% – вторым и 45 – третьим. Брак в первом цехе 1%, во втором – 1,5%, в третьем – 2%. Наугад выбранная продукция оказалась браком. Какова вероятность того, что она была произведена первым цехом.
Обозначим за 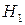 – продукция была выпущена в первом цехе,
– продукция была выпущена в первом цехе,  – во втором,
– во втором, 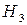 – в третьем. Очевидно, что
– в третьем. Очевидно, что 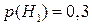 ;
;  ;
; 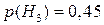 . Тогда
. Тогда  – брак был произведен в первом цехе (
– брак был произведен в первом цехе (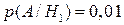 ),
),  – во втором (
– во втором (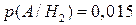 ),
),  – в третьем (
– в третьем (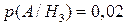 ). Тогда вероятность события А – извлечения черного шара – будет равна
). Тогда вероятность события А – извлечения черного шара – будет равна
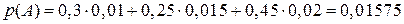
Из формулы Байеса следует, что 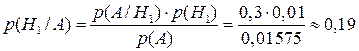 .
.