Содержание
1. Непрерывность функции в точке. Свойства функций, непрерывных в точке
2. Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке
3. Точки разрыва функции и их классификация
Непрерывность функции в точке. Свойства функций, непрерывных в точке
Определение 1. Функция 
называется непрерывной в точке 
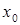, если выполнены следующие три условия: 1) 
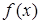определена в точке 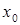и ее окрестности; 2) существует конечный предел функции 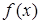в точке 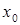; 3) этот предел равен значению функции в точке 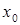, т. е.
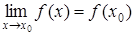
Так как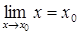 
, то равенство (1) можно записать в виде
Это означает, что для непрерывной функции знаки предела и функции можно переставлять.
На практике часто используется следующее определение непрерывности функции в точке, эквивалентное определению 1.
Определение 2. Функция называется непрерывной в точке 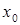, если: 1) 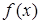определена в точке 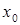и ее окрестности; 2) существует конечные односторонние пределы 
и 
; 3) эти пределы равны между собой и равны значению функции в точке 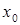, т. е.
Сформулируем еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.
Пусть функция определена в точке 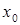и ее окрестности. Дадим аргументу 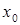приращение 
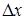. Тогда функция получит приращение 
(рис. 1).
Рис. 1. – Непрерывная функция
Определение 3. Функция называется непрерывной в точке 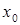, если: 1) 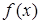определена в точке 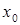и ее окрестности; 2) бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
Пример 1. Доказать, что функция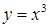 
непрерывна в любой точке области определения, т. е. в любой точке 
.
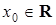Решение. Дадим аргументу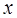 
приращение 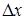в точке 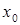и найдем приращение функции 
:
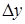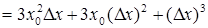
Следовательно,
.
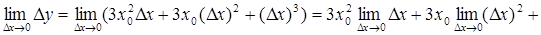
Таким образом, 
, а это и означает, что функция 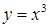непрерывна в точке .
Пример 2. Исследовать на непрерывность в точке 
следующие функции:
а) 
; б) 
в)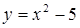 
.
Решение. а) Функция определена в окрестности точки , но в самой точке она не определена, следовательно, в этой точке она не является непрерывной (не выполнено первое условие непрерывности).
б) Для исследования на непрерывность воспользуемся определением 2. В точке функция 
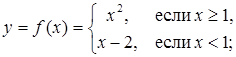определена (
), т. е. первое условие непрерывности выполнено; второе условие также выполняется: 
; 
; третье условие непрерывности не выполняется, так как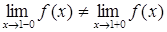 
. Следовательно, данная функция также не является непрерывной в точке .
в) Функция 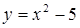является непрерывной в точке , так как выполнены все три условия непрерывности: она определена в точке 
и ее окрестности; существуют односторонние пределы 
, 
; эти пределы равны между собой и равны значению функции в точке : 
.
Свойства функций, непрерывных в точке:
1) Если функции 
и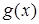 
непрерывны в точке 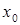, то функции 
, 
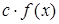(с – постоянная), 
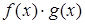и 
(при условии что 
) также непрерывны в точке .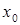
2) Если функция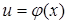 
непрерывна в точке 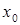, а функция 
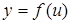непрерывна в точке 
, то сложная функция 
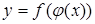непрерывна в точке .
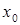Непрерывность функции на отрезке. Свойства функций, непрерывных на отрезке
Определение 4. Функция называется непрерывной на отрезке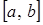 
, если она непрерывна в каждой точке этого отрезка (в точке a непрерывна справа, т.е. 
, а в точке b непрерывна слева, т. е. 
).
Все основные элементарные функции непрерывны в области их определения.
Свойства функций, непрерывных на отрезке:
1) Если функция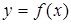 
непрерывна на отрезке 
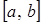, то она ограничена на этом отрезке (первая теорема Вейерштрасса).
2) Если функция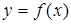 
непрерывна на отрезке 
, то на этом отрезке она достигает своего наименьшего значения 
и наибольшего значения 
(вторая теорема Вейерштрасса) (см. рис. 2).
3) Если функция 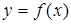непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка существует хотя бы одна точка 
такая, что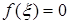 
(теорема Больцано-Коши).