Лекция
Тема: Свойства функций: монотонность, промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума)
Задание
1. По конспекту лекции ответить на ключевые вопросы темы:
1) Определите понятие возрастания функции. (Устно)
2) Определите понятие убывания функции. (Устно)
3) Какая функция называется монотонной? (Письменно)
4) Что называется экстремумом функции? (Письменно)
5) Что называется точкой максимума? (Письменно)
6) Что называется точкой минимума? (Письменно)
7) Продолжите предложение: «Функция выпукла вниз, если …»(Письменно)
8) Продолжите предложение: «Функция выпукла вверх, если …»(Письменно)
2. Законспектировать пример и решить задачу.
Конспект лекции
Определение 1:
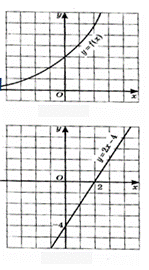
Функцию у= f(x) называют возрастающей на множестве Х, если для любых точек x1 и x 2 из множества Х, таких, что x1 < x 2, выполняется неравенство f (x1) < f (x 2 ).
Функция возрастает, если большему значению аргумента соответствует большее значение функции
Определение 2:
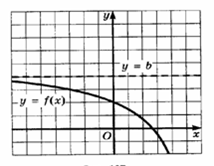Функцию у= f(x) называют убывающей на множестве Х, если для любых точек x1 и x2 из множества Х, таких, что x1 < x 2, выполняется неравенство f (x1) > f(x2)
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Определение 3: Число m называют наименьшим значением функции у= f(x) на множестве Х, если:
1)во множестве Х существует такая точка x0, что f(x0) = m
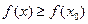2) для любого значения х из множества Х выполняется неравенство
|
|
Определение 4: Число т называют наибольшим значением функции у= f(x) на множестве Х, если:
1)во множестве Х существует такая точка, что f(x0) = т
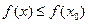2) для любого значения х из множества Х выполняется неравенство
Если у функции существует yнаиб, то она ограничена сверху
Если у функции существует yнаим, то она ограничена снизу.
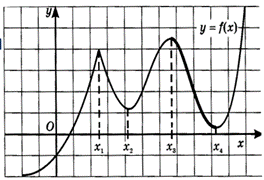
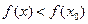Определение 5: Точку x0 называют точкой максимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
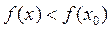Определение 6: Точку x0 называют точкой минимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
Точки максимума и минимума объединяют общим названием – точки экстремума.
Определение 7: Функция выпукла вниз на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
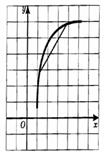
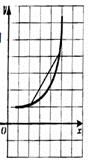Определение 7: Функция выпукла вверх на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
 |
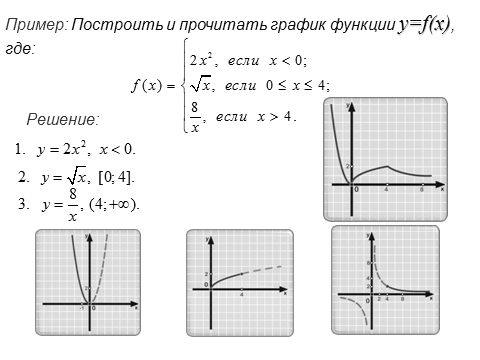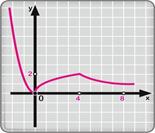1. Область определения функции — вся числовая прямая.
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция убывает на луче (-∞; 0], возрастает на отрезке [0; 4], убывает на луче [4; +∞).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим = 0 (достигается при х = 0), унаиб не существует.
6. Функция непрерывна.
|
|
7. Область значений функции — луч [0; +∞).
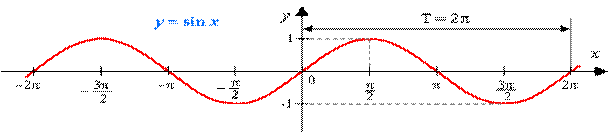
Задача: По графику функции y=sin x прочитать свойства функции.
Д.З. № 1463