Сущность метода проецирования.
· Центральное проецирование.
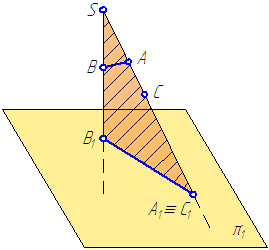Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB,>… — проецирующего луча).
Рисунок 1.1 – Центральное проецирование
Введём следующие обозначения (Рисунок 1.1):
S – центр проецирования (глаз наблюдателя);
π1 – плоскость проекций;
A, B, C – объекты проецирования – точки;
SA, SB – проецирующие прямые (проецирующие лучи).
Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.
Свойство 2. Проекция прямой есть прямая.
· Параллельное проецирование.
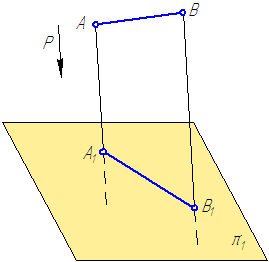Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P, называется параллельным .
Введём обозначения:
Р – направление проецирования;
π1 – горизонтальная плоскость проекций;
A, B – объекты проецирования – точки;
А 1 и В 1 – проекции точек А и В на плоскость проекций π1.
Параллельной проекцией точки называется точка пересечения проецирующей прямой, параллельной заданному направлению проецирования Р, с плоскостью проекций π1.
Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р. Проецирующий луч проведённый через точку А пересечёт плоскость проекций π1 в точке А 1. Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В 1. Соединив точки А 1 и В 1, получим отрезок А 1 В 1– проекция отрезка АВ на плоскость π1.
Свойства параллельного проецирования:
1. Проекции параллельных прямых параллельны.
Из рисунка видно, что прямые АА1, ВВ1, СС1 и DD1 образуют две параллельные плоскости a и b. Эти две плоскости пересекаются с П1. Следовательно, линии пересечения их А1В1 и С1D1 будут параллельны.
2. Если точка делит длину отрезка в отношении m:n, то проекция этой точки делит длину проекции отрезка в том же отношении.
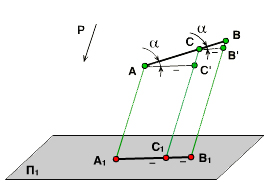
Пусть точка С принадлежит отрезку АВ, причем |АС|: |СВ| = 2: 1. Построим параллельную проекцию А1В1 отрезка АВ. Точка С1 
А1В1. Проведём АC’ || А1C1 и CB’ || C1B1, получим два подобных треугольника АCC’ и CBB’. Из их подобия следует пропорциональность сторон: |АC|: |СВ| = |AC’|: |CB’|, но |CB’| = |С1В1|, а |AC’| = |А1C1|, отсюда |АC|: |СВ| = |А1С1|: |C1B1|.
3. Плоская фигура, параллельная плоскости проекций, проецируется без искажения.
Ортогональные проекции.
Если направление проецирования Р перпендикулярно плоскости проекций p1, то проецирование называется прямоугольным или ортогональным, если Р не перпендикулярно π1, то проецирование называется косоугольным.
· Метод Монжа (эпюр).
Метод изображения объектов по Монжу заключается в двух основных моментах:
1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π1 и π2 (Рисунок 1.6).
Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте.
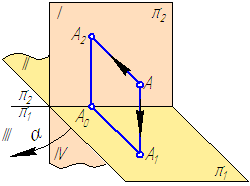Рисунок 1.6 – Модель построения проекций точки
π1 – горизонтальная плоскость проекций
π2 – фронтальная плоскость проекций
π1∩π2 — ось проекций (обозначим π2/π1)
2. Совместим поворотом вокруг оси проекций π2/π1 плоскости проекций в одну плоскость (π1 с π2), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным чертежом (Рисунок 1.7):
Рисунок 1.7 – Ортогональный чертеж
Прямая А 2 А 1 называется линией проекционной связи, которая соединяет разноимённые проекции точки (А 2 — фронтальную и А 1 — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А 2 А 1⊥π2/π1. На эпюре отрезки, обозначенные фигурными скобками, представляют собой:
- А 0 А 1 – расстояние от точки А до плоскости π2, соответствующее координате yА;
- А 0 А 2 – расстояние от точки А до плоскости π1, соответствующее координате zА.
· Изображение точки общего и частного положения на эпюре.
Точка не принадлежащая ни одной из плоскостей проекций - точка общего положения. Координаты точки общего положения не равны нулю (x≠0,y≠0,z≠0), и в зависимости от знака координаты точка может располагаться в одной из 4-ех четвертей.
Точка принадлежит плоскости проекций – точка частного положения.
· Изображение прямой частного и общего положения на эпюре.
Прямая, не параллельная ни одной из плоскостей проекций, называется прямой общего положения.
Прямая, параллельная (уровенная) или перпендикулярная (проецирующая) какой-либо плоскости проекций, называется прямой частного положения.
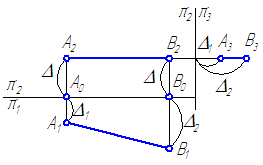
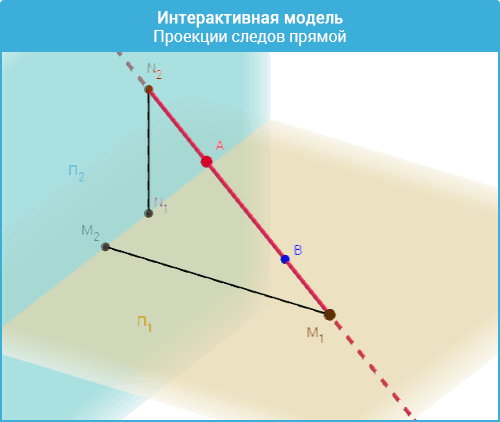Рисунок 2.3 – Эпюр фронтали(ур-я п.)
Рисунок 2.2 – Эпюр горизонтали(уров-я прямая)
· Построение следов прямой.
· Определение НВ прямой и угол наклона к проецирующим плоскостям
Истинная величина отрезка может быть найдена как гипотенуза прямоугольного треугольника, одним катетом которого является проекция этого отрезка на плоскость проекций (А2В2), а другим – разность координат концов этого отрезка до плоскости (Δ2), в которой ведется построение. Угол между истинной величиной (АВ) и проекцией (А2В2) определяет угол наклона (β) прямой к той плоскости проекций, в которой ведётся построение (Рисунок 2.6).
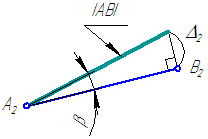
См. рисунок
Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π2
· Взаимное расположение прямых
Две прямые в пространстве могут быть:
- параллельными;
- пересекающимися;
- скрещивающимися.
· Теорема о проецировании прямого угла
Теорема. Если одна из сторон прямого угла параллельна какой-либо плоскости, а другая – этой плоскости не перпендикулярна, то на эту плоскость прямой угол проецируется в виде прямого угла.
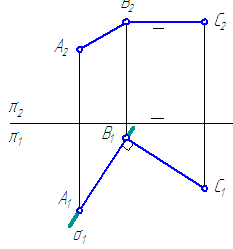
Способы задания плоскости.
· Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости: все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
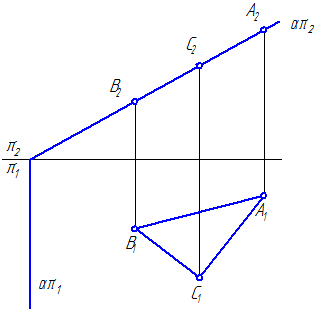
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
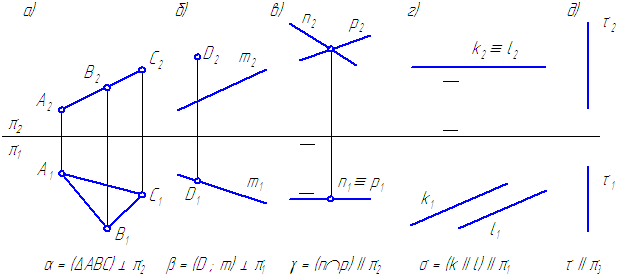
Рисунок 3.4 – Эпюры плоскостей частного положения
· 
Построение недостающей проекции.
См. рисунок
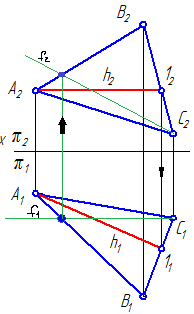
· Главные линии плоскости
Горизонталь(h) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1)
Фронталь(f) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2)
Линия наибольшего ската - это прямая, принадлежащая плоскости и перпендикулярная одной из линий уровня плоскости. С её помощью определяют угол наклона заданной плоскости к одной из плоскостей проекций.