Взаимное расположение плоскостей.

· Условие параллельности плоскостей

Две плоскости параллельны, когда две взаимно пересекающиеся прямые одной плоскости соответственно параллельны двум взаимно пересекающимся прямым другой плоскости.

 

 

· Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

1. Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
2. Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
3. Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.

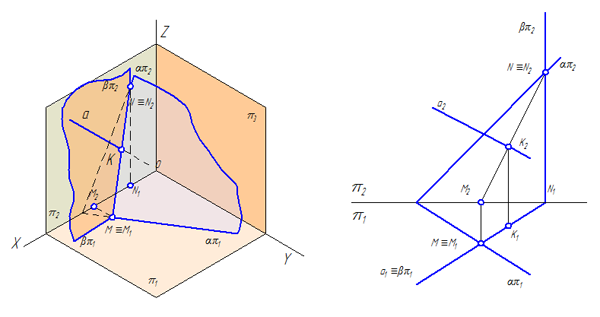
Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение:

1. Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ₁ (горизонтальный след плоскости);
2. Точка К должна принадлежать прямой АВ ⇒ К ₁∈ А ₁ В ₁ и заданной плоскости σ ⇒ К ₁∈σ₁, следовательно, К ₁ находится в точке пересечения проекций А ₁ В ₁ и σ₁;
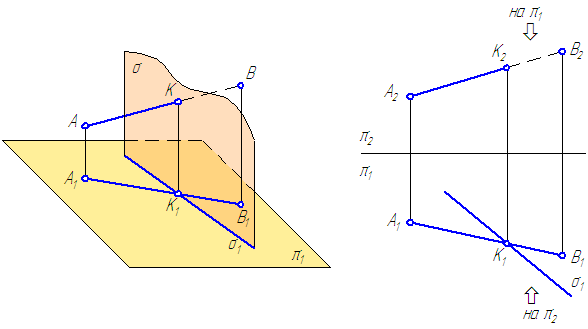3. Фронтальную проекцию точки К находим посредством линии проекционной связи: К ₂∈ А ₂ В ₂.

 

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = Δ АВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

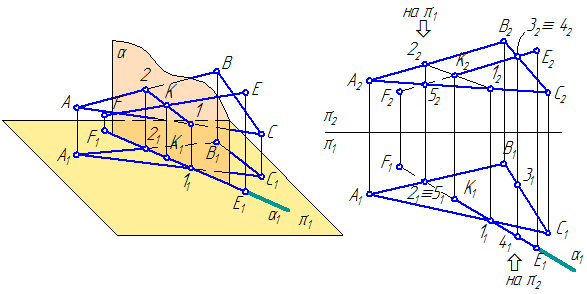
а	б

 

Рисунок 3.15 – Пересечение прямой с плоскостью

Решение:

1. Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
2. Если α⊥π₁, то на плоскость проекций π₁ плоскость α проецируется в прямую (горизонтальный след плоскости απ₁ или α₁), совпадающую с E ₁ F ₁;
3. Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
4. Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.

· Параллельность прямой плоскости

Признак параллельности прямой плоскости: прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости.

· Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

· Определение видимости методом конкурирующих точек:

См. рисунки

· Способ перемены плоскостей проекции.

См. рисунки

· Способ вращения.

См. рисунки

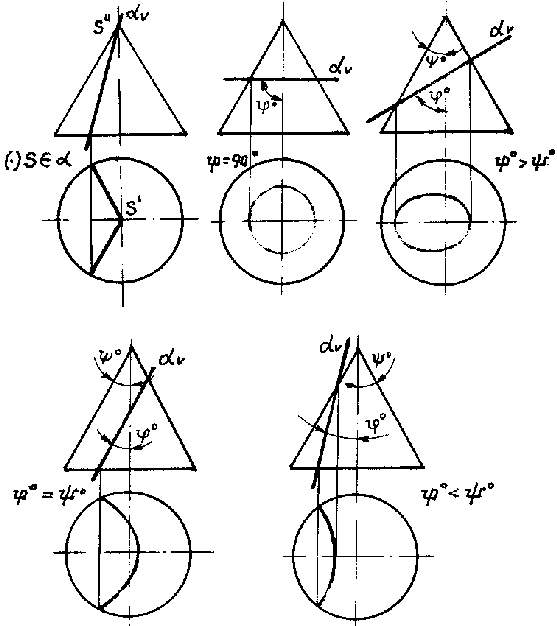Конические сечения

Взаимное пересечение поверхностей (см. гайды)

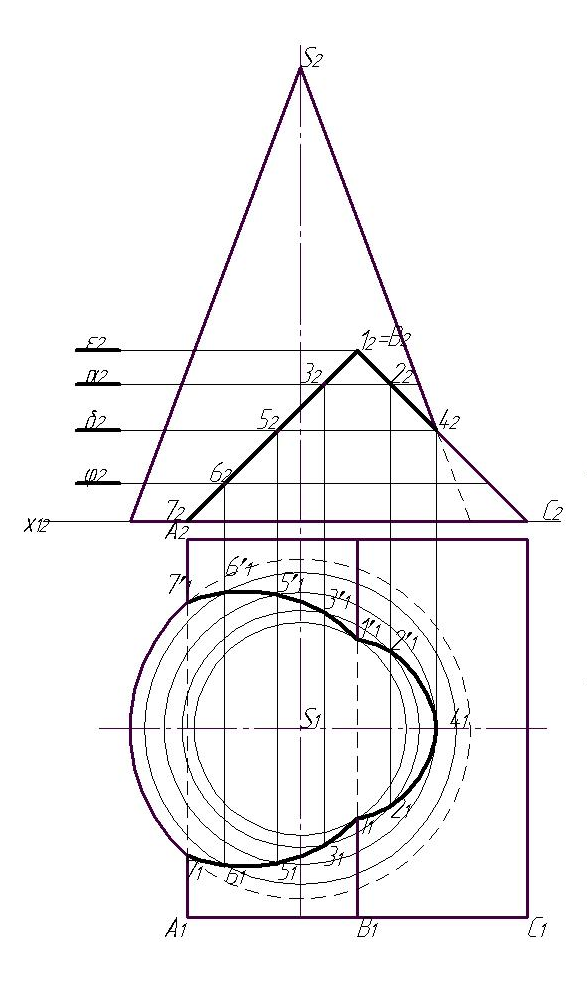
Развертка поверхностей

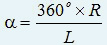
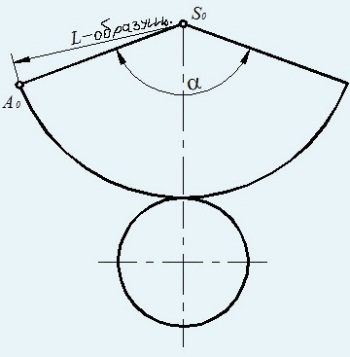Развертка пирамиды: см. рисунок

Развертка конуса:

 

 

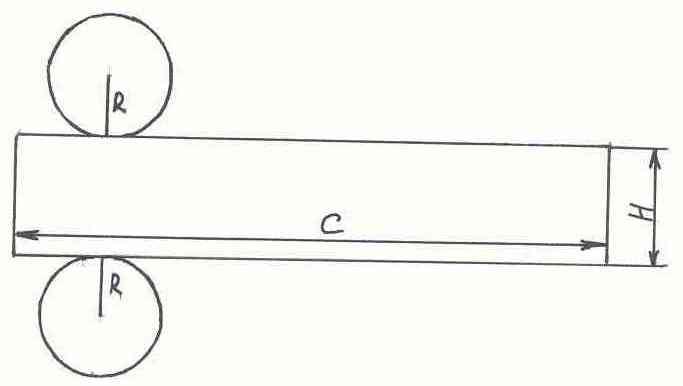
Развертка цилиндра: поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR

 

 

Аксонометрия

Прямоугольная изометрия Прямоугольная диметрия(0.5у)

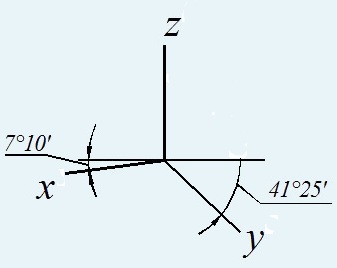
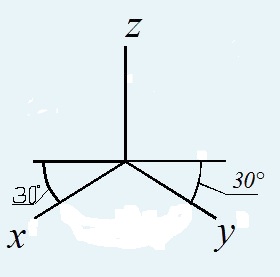
Косоугольные проекции

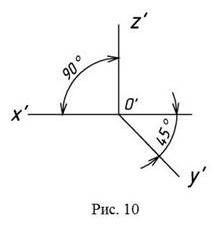· Фронтальная изометрическая проекция

 

 

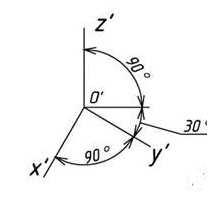Горизонтальная изометрическая проекция