Тема: Некоторые следствия из аксиом
На этом уроке мы рассмотрим некоторые следствия из аксиом. Рассмотрим и докажем теорему о том, что через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Рассмотрим и докажем теорему о том, что через две пересекающиеся прямые проходит плоскость, и притом только одна. Далее с помощью аксиом и двух теорем-следствий мы решим несколько задач
Предлагаю Вашему вниманию видео урок по ссылке:
https://www.youtube.com/watch?v=uockeNnyLSA
Условные обозначения:
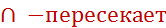
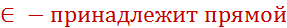
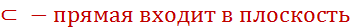
Материал учебника: с. 6-7 читать, разобрать, выучить следствия из аксиом.
Классная работа: Пользуясь видео уроком, в тетради сделать запись и начертить:
Теорема 1 и ее доказательство
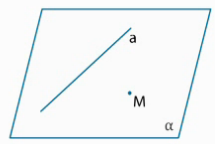
Рис. 2.
Дано: Прямая a, M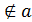 
Доказать: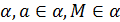 
1) Существует плоскость.
2) Плоскость α единственна
Доказательство первого пункта:
Докажем, что существует плоскость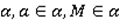 
. На прямой 
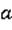Выберем любые две точки Р и Q: 
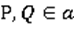. Тогда имеем 3 точки – Р, Q, M, которые не лежат на одной прямой.
По аксиоме А1, через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна, т.е. плоскость α, которая содержит и прямую a, и точку М, существует.
Доказательство второго пункта:
Следует доказать единственность такой плоскости.
Предположим, что существует иная плоскость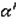 
, которая проходит и через точку М, и через прямую a. Например, это будет плоскость, проходящая через точки Q’и P’, прямой a, и точку M. Но тогда эта плоскость 
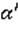проходит и через прямую a, и через точку М, а значит, и через точки Р, Q, M. А через три точки Р, Q, M, не лежащие на одной прямой, в силу 1 аксиомы, проходит только одна плоскость. Значит, эта плоскость 
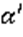совпадает с плоскостью 
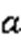. Значит, единственность доказана. Вся теорема доказана.
Теорема 2 и ее доказательство
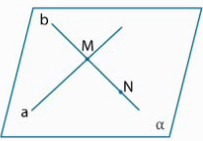
Рис. 3.
Дано: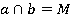 
Доказать:
1) Существует плоскость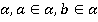 
.
2) Такая плоскость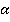 
единственна.
Доказательство:
На прямой b возьмем точку N, которая не совпадает с точкой М, то есть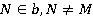 
.
Тогда имеем точку N, которая не принадлежит прямой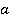 
. По предыдущей теореме, через прямую и не лежащую на ней точку проходит плоскость. Назовем ее плоскостью 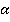. Значит, такая плоскость, которая проходит через прямую 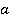и точку N, существует. Но эта плоскость также проходит и через всю прямую b, так как две точки М и N прямой b лежат в этой плоскости. То есть и прямая 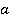и прямая b принадлежат плоскости 
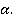Значит, существует такая плоскость, которая проходит через две пересекающиеся прямые, что и требовалось доказать в первом пункте.
Докажем единственность этой плоскости.
Предположим противное. Пусть существует иная плоскость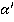 
, такая, которая проходит и через прямую 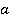, и через прямую b. Но тогда она также проходит и через прямую 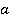, и точку N. Но по предыдущей теореме эта плоскость единственна, т.е. плоскость 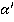совпадает с плоскостью .
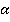Значит, мы доказали существование единственной плоскости, проходящей через две пересекающиеся прямые.
III. Закрепление изученного материала
1. Прочитать формулировки следствий из аксиом.
Записать решение задач из видео-урока
Подведение итогов
Мы повторили аксиомы стереометрии, познакомили со следствиями и применили их при решении задач..
Домашнее задание
Повторить аксиомы А1-А3.
Выучить следствия из аксиом .
Прочитать пункт 3.
Задачи 6,8,9