На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма. В информатике процесс решения задачи распределяется между двумя субъектами: программистом и компьютером. Программист составляет алгоритм (программу), компьютер его исполняет. В традиционной математике такого разделения нет, задачу решает один человек, который составляет алгоритм решения задачи и сам выполняет его. Сущность алгоритмизации не в том, что решение задачи представляется в виде набора элементарных операций, а в том, что процесс решения задачи разбивается на два этапа: творческий (программирование) и не творческий (выполнение программы). И выполняют эти этапы разные субъекты – программист и исполнитель.
При составлении алгоритма программист никому ничего не объясняет, а исполнитель не пытается ничего понять. Алгоритм размещается в памяти компьютера, который извлекает команды по одной и исполняет их. Человек действует по-другому. Чтобы решить задачу, человеку требуется держать в памяти метод решения задачи в целом, а воплощает этот метод каждый по-своему.
Практика программирования показала необходимость научно обоснованной методологии разработки и документирования алгоритмов и программ. Эта методология должна касаться анализа исходной задачи, разделения ее на достаточно самостоятельные части и программирования этих частей по возможности независимо друг от друга. Такой методологией, зародившейся в начале 70-х годов и получившей в последнее время широкое распространение, является структурное программирование. По своей сути оно воплощает принципы системного подхода в процессе создания и эксплуатации программного обеспечения ЭВМ. В основу структурного программирования положены следующие достаточно простые положения [8]:
|
|
1. алгоритм и программа должны составляться поэтапно (по шагам);
2. сложная задача должна разбиваться на достаточно простые, легко воспринимаемые части, каждая из которых имеет один вход и один выход;
3. логика алгоритма и программы должна опираться на минимальное число достаточно простых базовых управляющих структур.
Использование этих положений позволяет внести определенную систему в труд программиста и составлять удобочитаемые алгоритмы (и программы), которые легко изучать и проверять. Фундаментом структурного программирования является теорема о структурировании. Эта теорема устанавливает, что, как бы сложна ни была задача, схема соответствующей программы всегда может быть представлена с использованием весьма ограниченного числа элементарных управляющих структур. Элементарные структуры могут соединяться между собой, образуя более сложные структуры, по тем же самым элементарным схемам.
Базовыми элементарными структурами являются структуры: следование, ветвление и повторение (цикл), изображенные на рис.5. Они обладают функциональной полнотой, т.е. любой алгоритм может быть реализован в виде композиции этих трех конструкций.
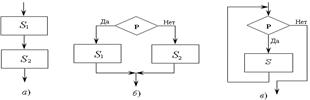
Рис. 5
Первая (а) структура - тип последовательность (или просто последовательность), вторая (б) – структура выбора (ветвление), третья (в) – структура цикла с предусловием.
При словесной записи алгоритма указанные структуры имеют соответственно следующий смысл:
|
|
«выполнить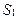 
; выполнить 
»,
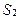если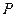 
, то выполнить 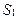, иначе выполнить »,
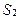«до тех пор, пока 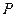, выполнять 
»,
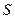где 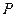- условие; 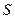, , 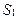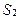- действия.
Рассматривая схему программы, можно выделить в ней части, достаточно простые и понятные по структуре. Представление этих фрагментов укрупненными блоками существенно облегчает восприятие алгоритма в целом.
Достаточно часто структурное программирование подразумевает использование более трех базисных структур. Применительно к языку Паскаль, в котором наиболее полно нашли свое отражение идеи структурного программирования, целесообразно при проектировании алгоритмов дополнительно использовать еще четыре элементарные структуры: сокращенную запись разветвления (рис. 16,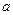 
); структуру варианта (рис. 16, 
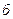); структуру повторения или цикла с параметром (рис. 16, 
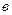); структуру цикла с постусловием (рис. 6, 
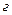). Каждая из этих структур имеет один вход и один выход. В языке Паскаль имеются средства, позволяющие непосредственно реализовывать в программе любую из этих структур, поэтому правильное использование типовых структур в процессе разработки алгоритма обеспечивает упрощение этапов решения задачи на ЭВМ.
Рис. 6
Ветвящимся (разветвляющимся) называется вычислительный процесс, в котором происходит выбор одного из возможных вариантов вычислений в зависимости от проверки заданных условий.
В зависимости от типа и числа проверяемых условий различают:
- ветвление с простым условием (условие - выражение отношения);
- ветвление с составным условием (условие - логическое выражение);
- сложное ветвление (несколько условий).
|
|
Вариант вычислений, определяемый в результате проверки условия, называется ветвью.
При необходимости одновременного выполнения нескольких операций отношения они объединяются в составное условие в виде логического выражения. Для этой цели используют логические операции:
- 
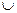- логическое сложение (ИЛИ), дизъюнкция;
- 
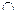- логическое умножение (И), конъюнкция;
- I - отрицание (не).
Циклическим называется процесс многократного повторения некоторого участка вычислений при изменении хотя бы одной из входящих в него величин.
Повторяющийся участок вычисления называется циклом. Операции, осуществляемые в цикле, составляют тело цикла.
Величина, изменяющая своё значение от цикла к циклу, называется параметром цикла.
Зависимость, связывающая текущее и предыдущее значения параметра цикла, определяет закон изменения параметра цикла.
Зависимость, предписывающая повторение цикла, либо выход из него, называется условием повторения цикла.
Все циклические процессы по признаку определения количества повторений (М) разделяются на два класса.
Арифметическим называется циклический процесс, число повторений в котором может быть определено заранее, т.е. не зависит от результатов счёта в челе цикла.
Итерационным является циклический процесс, число повторений в котором зависит от результатов вычислений в теле цикла и не может быть определено заранее.
Независимо от того, к какому классу относится вычислительный процесс, каждый из них содержит обязательные элементы:
- вход в цикл (формирование начального значения параметра цикла);
- вычисления в теле цикла (расчёт текущего значения функций, формирования нового значения параметра цикла, а также вспомогательные операции);
- выход из цикла (проверка условия, определяющего повторение вычислений, либо их прекращение).
По своему содержанию эти элементы зависят от класса и особенностей цикла, в котором используются.
В соответствии с видом задания (изменения) параметра цикла арифметические циклы подразделяются на:
- циклы с аналитическим изменением параметра;
- циклы с табличным заданием параметра.
Выполнение арифметических циклов, т.е. многократное вычисление значений функции при изменяющихся значениях аргумента, называется табуляцией функции.
Список использованной литературы
1. Акулов О.А. Информатика: учебник / О.А. Акулов, Н.В. Медведев. – М.: Омега-П, 2007. – 270 с.
2. Алексеев А.П. Информатика 2007 / А.П. Алексеев. – М.: СОЛОН-ПРЕСС, 2007. – 608 с.
3. Вьюхин В.В. Информатика и вычислительная техника: учеб. пособие для инженерных специальностей / В.В. Вьюхин; под ред. В.Н. Ларионова. - М.: Дрофа, 1992. – 286 с.
4. Гейн А.Г. Основы информатики и вычислительной техники / А.Г. Гейн. - М.: Просвещение, 1992. – 245 с.
5. Информатика: практикум по технологии работы на компьютере / под ред. Н.В. Макаровой. - 2-е изд. - М.: Финансы и статистика, 1998. – 384 с.
6. Макарова Н.В. Информатика: практикум по технологии работы на компьютере / Н.В. Макарова, С.Н. Рамин. – М.: Академия, 1997. – 384 с.
7. Макарова Н.В. Информатика: учеб. пособие для вузов / Н.В. Макарова, Н.В. Бройдо. – М.: Академия, 2003. – 768 с.
8. Могилев А.В. Информатика: учеб. пособие для вузов / А.В. Могилев, Н.И. Пак, Е.К. Хеннер; под ред. Е.К. Хеннера. - М.: Академия, 2000. – 346 с.
9. Острейковский В.А. Информатика / В.А. Острейковский. М.: Высш. шк., 2000. – 235 с.
10. Угринович Н.Д. Практикум по информатике и информационным технологиям: учеб. пособие для общеобразовательных учреждений / Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова. – М.: Бином, 2002. – 400 с.