Группа 14 Дата 28.10.21
Цель урока: ввести понятие мгновенной скорости; научить определять относительную скорость движения; научить применять физические законы при решении задач
Задачи урока: обучающая: обеспечить восприятие, осмысление и первичное запоминание учащимися понятий мгновенная скорость; обобщить знания о понятии «прямолинейное равноускоренное движение», проверить применение на практике изученного материала;
развивающая: развивать мыслительную деятельность посредством постановки проблемных вопросов: наблюдение, память, внимание, анализ, обобщение, умение делать выводы;
воспитательная: воспитать навыки творческого усвоения и применения знаний, интерес к физике, расширять кругозор учащихся.
Ход урока:
Ⅰ. Проверка домашнего задания.
1. Принцип относительности в механике.
2. Сформулируйте закон сложения скоростей.
3. Чем относительная скорость отличается о абсолютной?
4. Задача. Скорость лифта в высотном здании 3 м/с. Начертите график перемещения. Определите по графику время в течение которого лифт достигнет 90 м(26 этажа)
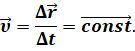ⅠⅠ. Изучение нового материала.
Самым простым видом механического движения является прямолинейное движение с постоянной по модулю и направлению скоростью:
Равномерно движение — это модель реального движения, в действительности же реальные тела движутся не равномерно: автомобиль в начале своего движения из состояния покоя постепенно увеличивает свою скорость. Где-то в середине пути он, возможно, будет недолго двигаться с постоянной скоростью. А при торможении его скорость будет постепенно уменьшаться. То есть движение автомобиля является неравномерным. Поэтому описать его с помощью уравнения движения мы не можем, так как скорость тела постоянно меняется.
|
|
Но нам на помощь приходить понятие мгновенной скорости, то есть скорости точки в данный момент времени (или в данной точке траектории).
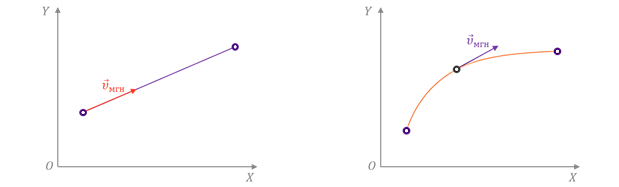
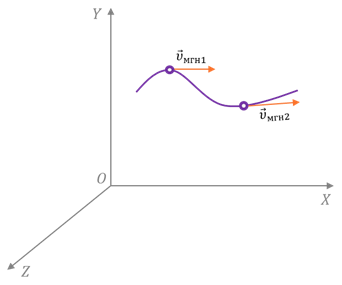Чтобы понять, как определяется мгновенная скорость, рассмотрим неравномерное движение материальной точки по криволинейной траектории. Пусть в некоторый момент времени t она занимает положение М. А спустя некоторый промежуток времени Δ t 1 — положение М 1. Укажем на рисунке перемещение, которое совершила точка за этот промежуток времени. Разделим это перемещение на промежуток времени, в течение которого оно произошло и найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени. Эта скорость называется средней скоростью перемещения. Она показывает, какое перемещение в среднем совершала точка за единицу времени. 
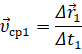Направление этой скорости совпадает с направлением вектора перемещения точки.
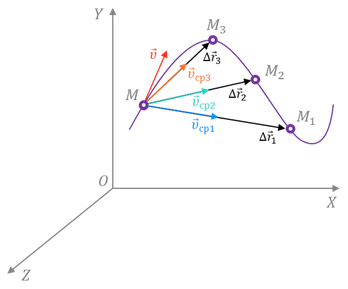Определим скорость точки в положении М - уменьшим рассматриваемый промежуток времени. В этом случае точка совершит меньшее перемещение. Средняя же скорость точки на этом участке хотя и не равна скорости в точке М, но уже ближе к ней. Продолжим уменьшать промежутки времени и перемещения, и придём к тому, что средние скорости будут незначительно отличаться друг от друга и от скорости точки в положении М. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время. Следовательно, при стремлении промежутка времени к нулю отношение 
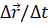будет стремиться к своему некоторому предельному значению.
|
|
Физическая векторная величина, равная пределу отношения перемещения к промежутку времени, в течение которого это перемещение произошло, при стремлении промежутка времени к нулю, называется мгновенной скоростью:
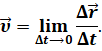
Направление вектора мгновенной скорости зависит от вида движения точки. Так, если точка движется прямолинейно, то направление мгновенной скорости совпадает с направлением движения. А вот в случае криволинейного движения вектор мгновенной скорости направлен по касательной к траектории.
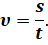Для описания неравномерного движения точки, помимо понятия средней скорости перемещения, в физике чаще используют понятие средней путевой скорости. Она определяется отношением пути к промежутку времени, за который этот путь пройдён:
Проще говоря, средняя путевая скорость показывает, какой путь в среднем проходило тело за единицу времени. Однако не стоит забывать о том, что средняя путевая скорость характеризует движение за весь промежуток времени в целом. Например, когда мы слышим, что расстояние между двумя городами автомобиль преодолел за 5 ч со скоростью 100 км/ч, мы понимаем, что в среднем он за каждый час проезжал сто километров. Но во время движения он мог заехать на заправку, где-то двигаться с бо́льшей или меньшей скоростью. Иными словами, средняя путевая скорость не даёт информации о скорости движения точки в каждый момент времени.
Ⅲ.Решение задач.
Задача 1. Определите среднюю путевую скорость движения точки, если первую половину пути она преодолела со скоростью 15 м/с, а вторую — со скоростью 25 м/с.
Ⅳ. Домашнее задание
Изучить §8, выполнить письменно стр.33 ЕГЭ