Вычисление площадей плоских фигур с помощью определенного интеграла
Пусть 
определена на отрезке 
. Разобьём на части несколькими произвольными точками: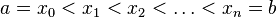 
.
Тогда говорят, что произведено разбиение 
отрезка 
Далее выберем произвольную точку 
, 
.
Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга
разбиения к нулю 
, если он существует независимо от разбиения и выбора точек 
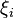, то есть
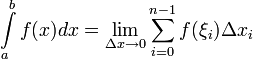
Если существует указанный предел, то функция называется интегрируемой на по Риману.
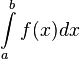
— нижний предел.
— верхний предел.
— подынтегральная функция.
— длина частичного отрезка.
— интегральная сумма от функции на соответствующей разбиению .
— максимальная из длин частичных отрезков.
Определённый интеграл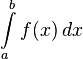 
численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a и x=b и графиком функции .
Пример:
Вычислить площадь фигуры, ограниченной линиями 
, 
, 
, 
.
При построении чертежа сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
Выполним чертеж (обратите внимание, что уравнение задает ось 
):
Решение продолжается так:
На отрезке 
график функции расположен над осью , поэтому:
Ответ: 
Понятие о дифференциальном уравнении. Общее и частное решение. Задача Коши. Задача о построении математическом модели демографического процесса.
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе.
|
|
Производные от элементарных функций выражаются через элементарные функции. Интегралы от элементарных функций часто не выражаются через элементарные функции. С дифференциальными уравнениями дело обстоит еще хуже. В результате решения можно получить:
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при 
, а решение отыскивается при 
.
Говорят, что задача Коши имеет единственное решение, если она имеет решение 
и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки 
имеет поле направлений, совпадающее с полем направлений . Точка задаёт начальные условия.
Пусть в области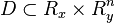 
рассматривается задача Коши:
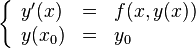
где 
. Пусть правая часть является непрерывной функцией в 
. В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши: Пусть a>0 и b>0 таковы, что замкнутый прямоугольник
принадлежит области D, тогда на отрезке 
, где 
, 
, существует решение задачи Коши.
Указанный отрезок называется отрезком Пеано. Заметим, что, локальный характер теоремы Пеано не зависит от гладкости правой части. Например, для 
и для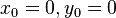 
решение 
существует лишь на интервале 
. Также отметим, что без дополнительных предположений относительно гладкости правой части, нельзя гарантировать единственность решения задачи Коши. Например, для 
возможно более одного решения.
|
|
Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x, y) удовлетворяет условию Липшица на D относительно y, если существует постоянная L такая, что
для всех 
.
Пусть правая часть f(x, y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.
Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.
Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию
где A>0 — константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.