Классическим методом частотного анализа сигналов является преобразование Фурье, суть которого можно выразить формулой (1)
 |
Результат преобразования Фурье – амплитудно-частотный спектр, по которому можно определить присутствие некоторой частоты в исследуемом сигнале.
В случае, когда не встает вопрос о локализации временного положения частот, метод Фурье дает хорошие результаты. Но при необходимости определить временной интервал присутствия частоты приходится применять другие методы.
Одним из таких методов является обобщенный метод Фурье (локальное преобразование Фурье). Этот метод состоит из следующих этапов:
1. в исследуемой функции создается “окно” – временной интервал, для которого функция f(x)¹0, и f(x)=0 для остальных значений;
2. для этого “окна” вычисляется преобразование Фурье
3. “ окно” сдвигается, и для него также вычисляется преобразование Фурье
“Пройдя” таким “окном” вдоль всего сигнала, получается некоторая трехмерная функция, зависящая от положения “окна” и частоты.
Данный подход позволяет определить факт присутствия в сигнале любой частоты, и интервал ее присутствия. Это значительно расширяет возможности метода по сравнению с классическим преобразованием Фурье, но существуют и определенные недостатки. Согласно следствиям принципа неопределенности Гейзенберга в данном случае нельзя утверждать факт наличия частоты w0 в сигнале в момент времени t0 - можно лишь определить, что спектр частот (w1,w2) присутствует в интервале (t1,t2). Причем разрешение по частоте (по времени) остается постоянным вне зависимости от области частот (времен), в которых производится исследование. Поэтому, если, например, в сигнале существенна только высокочастотная составляющая, то увеличить разрешение можно только изменив параметры метода. В качестве метода, не обладающего подобного рода недостатками, был предложен аппарат вейвлет анализа. [2]
Основные положения вейвлет-анализа
Различают дискретный и непрерывный вейвлет анализ, аппарат которых можно применять как для непрерывных, так и для дискретных сигналов.
Cигнал анализируется путем разложения по базисным функциям, полученным из некоторого прототипа путем сжатий, растяжений и сдвигов (2). Функция-прототип называется анализирующим (материнским) вейвлетом.
Вейвлет - функция должна удовлетворять 2-м условиям:
1. Среднее значение (интеграл по всей прямой) равен 0.
2. Функция быстро убывает при t ® ∞.
Обычно, функция-вейвлет обозначается буквой ψ.
В общем случае вейвлет преобразование функции f(t) выглядит так:
 (2)
(2)
где t – ось времени, x – момент времени, s – параметр, обратный частоте, a (*) – означает комплексно-сопряженное.
 |
Главным элементом в вейвлет анализе является функция-вейвлет. Вообще говоря, вейвлетом является любая функция, отвечающая двум вышеуказанным условиям. Наибольшей популярностью пользуются два изображенных на рисунке 1 вейвлета:
Рис 1. Примеры вейвлетов.
Сверху изображен вейвлет “сомбреро” (Mexican Hat), названный так благодаря своему внешнему виду. На нижней части рисунка 1 изображен вейвлет Морле. График любого вейвлета выглядит примерно также, как и вейвлет Морле. Заметим, что вейвлет Морле – комплекснозначный, на рисунке изображены его вещественная и мнимая составляющие.
Итак, у нас имеется некоторая функция f(t), зависящая от времени. Результатом ее вейвлет-анализа будет некоторая функция W(x,s), которая зависит уже от двух переменных: от времени и от частоты (обратно пропорционально). Для каждой пары x и s рецепт вычисления вейвлет преобразования следующий:
1. Функция вейвлет растягивается в s раз по горизонтали и в 1/s раз по вертикали.
2. Далее он сдвигается в точку x. Полученный вейвлет обозначается ψ(x,s).
3. Производится усреднение в окрестности точки s при помощи ψ(x,s).
В результате “вырисовывается” вполне наглядная картина, иллюстрирующая частотно-временные характеристики сигнала. По оси абсцисс откладывается время, по оси ординат – частота (иногда размерность оси ординат выбирается так: log(1/s), где s-частота), а абсолютное значение вейвлет преобразования для конкретной пары x и s определяет цвет, которым данный результат будет отображен (чем в большей степени та или иная частота присутствует в сигнале в конкретный момент времени, тем темнее будет оттенок).
 |
Рис 2. Вейвлет преобразование стационарного сигнала.
Данный рисунок показывает результаты вейвлет анализа для сигнала, представляющим из себя наложение двух синусоид различной частоты. Частотные характеристики данного сигнала не меняются во времени (сигнал стационарный), что хорошо видно на верхней части рисунка 2.
 |
Рис 3. Сравнение методов анализа.
По рисунку 3 удобно сравнить результаты, которые дают преобразование Фурье и вейвлет преобразование. Исходный сигнал изображен на рис (3a). Как видно из рис (3c) преобразование Фурье дает информацию о том спектре частот, который присутствует в сигнале в промежутке времени от 0 до 1 сек., при этом нам неизвестно когда именно та или иная частота реально присутствовала в сигнале.
В то же время вейвлет преобразование (3b) дает исчерпывающую картину динамики изменения частотных характеристик во времени. Все это указывает на то, что вейвлет преобразование существенно более информативно по сравнению с преобразованием Фурье.
3.3.1 Методы вычисления непрерывного вейвлет-преобразования.
Существует два разных пути проведения вейвлет преобразования. Речь идет о расчетах во временной и частотной областях. При работе во временной области мы имеем дело с функциями, аргументами которых являются временные параметры, а в случае частотной – частотные. В частотной области используется механизм быстрого преобразования Фурье. [5c]
3.3.1.1 Во временной области
Прежде всего, нам необходимо определить материнский вейвлет. Допустим, мы выбрали некоторую функцию, удовлетворяющую необходимым условиям: ψ0(η), где η – безразмерный период.
Итак, нам дана временная серия X, со значениями xn, в моменты времени nÎ[0,N-1], где N – количество измерений. Каждая величина разделена по времени на постоянную величину dt. Получив основную формулу для материнского вейвлета, необходимо иметь возможность изменять размеры вейвлета. Для этого строится так называемый "масштабированный" вейвлет который будет иметь вид:

 (3)
(3)
s – параметр, обратный частоте.
Вычисление вейвлет преобразования является сверткой искомой временной серии с функцией-вейвлетом. Основная формула имеет вид:
 (4)
(4)
в данном случае (*) – означает комплексно-сопряженное.
Результатом расчета Wn(s) по формуле (4)будет комплексное число. В качестве конечного результата берется абсолютное значение полученного комплексного числа. [5a]
Блок – схема алгоритма:
 |
 нет
нет
 |

да
|

 нет
нет
 |
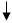 да
да
|
3.3.1.2 В частотной области
Вейвлет преобразование можно провести в частотной области. Для этого снова в первую очередь необходимо определить материнский вейвлет. Расчет по данной схеме происходит следующим образом: преобразование Фурье самого вейвлета (в данном случае будем рассматривать вейвлет Морле) сконцентрировано вокруг некоторой выделенной частоты w0 ≠ 0. Поэтому преобразование Фурье вейвлета, растянутого в s раз, будет сконцентрировано вокруг частоты w0/s (см рис. 4).
 |
Рис 4. Преобразование Фурье функции вейвлета.
Так как свертка функций эквивалентна их перемножению в частотной области, “строка” s = const на изображении вейвлет преобразования показывает эволюцию изучаемой функции на частотах, близких w0/s. То есть умножение Фурье-спектра исходной функции на пик в точке w0/s в частотной области (то есть на Фурье-образ растянутого вейвлета) вырезает из этой функции все то, что дает вклад в ее спектр на частотах, близких w0/s. В результате получается развертка спектрального компонента во времени. [1]
Основные формулы имеют вид:
 (5)
(5)
где (*) – означает комплексно-сопряженное, а знак (^) – преобразование Фурье.
 (6)
(6)
 (7)
(7)
Блок – схема алгоритма:
 |
 нет
нет
 |

да
|

 нет
нет
 |
 да
да
|
3.3.2 Выбор материнского вейвлета
В качестве материнского вейвлета подходит любая функция, удовлетворяющая двум вышеуказанным условиям. Для реализации алгоритма в качестве анализирующего вейвлета было решено воспользоваться вейвлетом Морле (рис. 5). Это было сделано по трем причинам:
· вейвлет Морле один из наиболее популярных [1] и широко применяется
· он обладает значительной наглядностью
· он прост в вычислительном плане, что ускоряет работу алгоритма
 |
рис 5. Вейвлет Морле.
Фактически вейвлет Морле является произведением комплексной синусоиды на гауссиан.
 , (8)
, (8)
где y является значением вейвлет функции с безразмерным периодом h, а w0 - волновой параметр (при реализации w0=6).
Необходимо также отметить, что вейвлет Морле является комплекснозначным, то есть имеет действительную и мнимую части.